Chúng tôi giới thiệu Giải bài tập Toán lớp 12 Bài 3: Phương trình đường thẳng trong không gian chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập phương trình đường thẳng trong không gian lớp 12.
Giải bài tập Toán lớp 12 Bài 3: Phương trình đường thẳng trong không gian
Phương pháp giải:
Ba điểm thẳng hàng nếu hai trong ba véc tơ cùng phương.
Do đó chỉ cần kiểm tra hai véc tơ bất kì cùng phương, sử dụng lý thuyết cùng phương nếu tồn tại một số thực sao cho .
Lời giải:
Do đó ba điểm luôn thẳng hàng.
Trả lời câu hỏi 2 trang 84 SGK Hình học 12: Cho đường thẳng có phương trình tham số . Hãy tìm tọa độ của một điểm trên và tọa độ một vecto chỉ phương của .Phương pháp giải:
Đường thẳng đi qua điểm và nhận làm VTCP.
Lời giải:
1 điểm thuộc là: và 1 vecto chỉ phương của là
Trả lời câu hỏi 3 trang 84 SGK Hình học 12: Cho hai đường thẳng d và d' có phương trình tham số lần lượt là: vàa) Hãy chứng tỏ điểm là điểm chung của và ;
b) Hãy chứng tỏ và có hai vecto chỉ phương không cùng phương.
Phương pháp giải:
a) - Thay tọa độ điểm vào phương trình đường thẳng , nếu tìm được thì thuộc .
- Thay tọa độ điểm vào phương trình đường thẳng , nếu tìm được thì thuộc .
b) Tìm hai VTCP của mỗi đường thẳng và nhận xét.
Lời giải:
a) Thay tọa độ của vào phương trình của ta được:
Do đó .
Thay tọa độ của vào phương trình của ta được:
Do đó .
Vậy là điểm chung của và .
b) Ta thấy là hai vecto không tỉ lệ nên hai veco đó không cùng phương.
Trả lời câu hỏi 4 trang 86 SGK Hình học 12: Chứng minh hai đường thẳng sau đây trùng nhau:
và
Phương pháp giải:
- Kiểm tra hai véc tơ chỉ phương cùng phương.
- Tìm một điểm thuộc cả hai đường thẳng.
Lời giải:
Ta thấy:
Có . Thay tọa độ của vào ta được:
Do đó nên trùng với
Phương pháp giải:
Cho đường thẳng và mặt phẳng .
Xét phương trình
+) Nếu phương trình có nghiệm duy nhất thì cắt .
+) Nếu phương trình vô nghiệm thì song song .
+) Nếu phương trình vô số nghiệm thì nằm trong .
Lời giải:
a) Xét phương trình:
(vô nghiệm) ⇒ mặt phẳng và không có điểm chung.
b) Xét phương trình:
(vô số nghiệm) .
c) Xét phương trình:
⇒ mặt phẳng và có điểm chung.
a) đi qua điểm có vec tơ chỉ phương ;
b) đi qua điểm và vuông góc với mặt phẳng có phương trình: ;
c) đi qua điểm và song song với đường thẳng có phương trình: ;
d) đi qua hai điểm và .
Phương pháp giải:
a) Phương trình tham số của đường thẳng d đi qua và có VTCP là:
b) Đường thẳng d vuông góc với mặt phẳng thì
c) Đường thẳng d song song đường thẳng ∆ thì
d) Đường thẳng d song song đường thẳng ∆ thì
Lời giải:
a) Phương trình đường thẳng có dạng: , với .
b) Đường thẳng vuông góc với mặt phẳng nên có vectơ chỉ phương .
Vậy phương trình tham số của có dạng:
c) Ta có: là vectơ chỉ phương của . Vì nên cũng là vectơ chỉ phương của . Phương trình tham số của có dạng:
d) Đường thẳng đi qua hai điểm và nên nhận là 1 VTCP.
Vậy phương trình tham số có dạng:
Chú ý:
Các em cũng có thể chọn Q làm điểm đi qua thì sẽ được phương trình
Hai phương trình này nhìn qua có khác nhau nhưng đều là phương trình tham số của cùng một đường thẳng.
a) ;
b) .
Phương pháp giải:
Cách 1:
Phương pháp viết phương trình hình chiếu của đường thẳng trên mặt phẳng :
Bước 1: Viết phương trình mặt phẳng chứa và vuông góc với ).
- .
- (với M là một điểm bất kì).
Bước 2: . Viết phương trình đường thẳng .
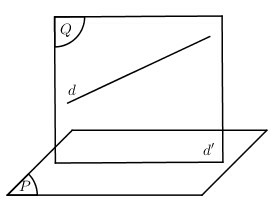
Cách 2:
Lấy 2 điểm bất kì thuộc d, gọi lần lượt là hình chiếu vuông góc của A, B trên (P). Khi đó chính là đường thẳng .
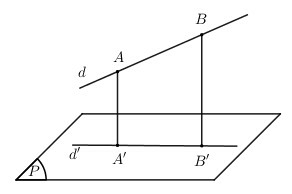
Lời giải:
a) Gọi là mặt phẳng vuông góc và chứa .
Khi đó là hình chiếu của lên .
Phương trình mặt phẳng có dạng: ; vectơ (0 ; 0 ;1) là vectơ pháp tuyến của .
Ta có: là vectơ pháp tuyến của .
Phương trình mặt phẳng có dạng: .
Chọn .
.
Đường thẳng đi qua và nhận làm VTCP nên .
Cách khác:
+) t = 0 ⇒ điểm M(2; -3; 1) ∈ d
+) t = 1 ⇒ điểm N(3; -1; 4) ∈ d.
Hình chiếu của M trên (Oxy) là M’(2 ; -3 ; 0).
Hình chiếu của N trên (Oxy) là : N’(3 ; -1 ; 0).
⇒ Hình chiếu của d trên (Oxy) là đường thẳng d’ đi qua M’ và N’.
⇒ d’ đi qua M'(2;-3;0) và nhận là 1 vtcp.
b) Mặt phẳng có phương trình .
Lấy và .
+) Hình chiếu vuông góc của trên là '.
+) Hình chiếu vuông góc của trên là chính nó.
Đường thẳng qua chính là hình chiếu vuông góc của lên .
Ta có: // .
Phương trình có dạng: .
a) d: và d': ;
b) d: và d':
Phương pháp giải:
Vị trí tương đối giữa hai đường thẳng d và d'. Gọi lần lượt là VTCP của d và d', .
Điều kiện để hai đường thẳng d và d' song song: .
Điều kiện để hai đường thẳng d và d' cắt nhau là và .
Điều kiện để hai đường thẳng d và d' chéo nhau: .
Lời giải:
a) Đường thẳng đi qua và có vectơ chỉ phương .
Đường thẳng đi qua và có vectơ chỉ phương .
Ta nhận thấy , không cùng phương nên d và d' chỉ có thể cắt nhau hoặc chéo nhau.
Ta có ;
Mà nên và cắt nhau.
Cách khác:
Xét hệ phương trình:
Từ (1) với (3), trừ vế với vế ta có , thay vào (1) có .
Từ đó và có điểm chung duy nhất . Do đó d và d' cắt nhau tại M.
b) Ta có : là vectơ chỉ phương của d và là vectơ chỉ phương của d' .
Ta thấy và cùng phương nên d và d' chỉ có thể song song hoặc trùng nhau.
Lấy điểm , thay tọa độ điểm vào phương trình ta được:
Vậy nên và song song.
Phương pháp giải:
Trong không gian Oxyz cho hai đường thẳng và .
Hai đường thẳng d và d' cắt nhau khi và chỉ khi hệ phương trình ẩn t, t' sau:
có đúng 1 nghiệm.
Lời giải:
Xét hệ
Hai đường thẳng d và d' cắt nhau khi và chỉ khi hệ có nghiệm duy nhất.
Giải (2) và (3) ta có ; . Thay vào phương trình (1) ta có .
Vậy thì d và d' cắt nhau.
a) d: và ;
b) d: và ;
c) d: và .
Phương pháp giải:
Phương pháp tìm giao điểm của đường thẳng và mặt phẳng .
Gọi .
Thay tọa độ điểm M vào phương trình mặt phẳng (P), tìm ẩn t, sau đó suy ra tọa độ điểm .
Lời giải:
a) Gọi .
Giả sử thì ta có:
.
Vậy .
b) Gọi .
Giả sử thì ta có:
, phương trình vô nghiệm.
Chứng tỏ và không cắt nhau hay .
c) Gọi .
Giả sử thì ta có:
Phương trình này có vô số nghiệm, chứng tỏ .
.
Phương pháp giải:
Chứng minh .
Khi đó .
Công thức tính khoảng cách từ điểm đến mặt phẳng là:
Lời giải:
Đường thẳng qua điểm có vectơ chỉ phương .
Mặt phẳng có vectơ pháp tuyến .
Ta có và nên .
Do vậy
= .
Cách khác:
Có thể chứng minh bằng cách:
Xét phương trình:
Phương trình vô nghiệm
.
Bài 7 trang 91 SGK Hình học 12: Cho điểm và đường thẳng : .
a) Tìm tọa độ điểm là hình chiếu vuông góc của điểm trên đường thẳng .
b) Tìm tọa độ điểm đối xứng với qua đường thẳng .
Phương pháp giải:
a) Gọi H là hình chiếu vuông góc của A trên đường thẳng thì , tham số hóa tọa độ điểm H theo ẩn t.
, giải phương trình tìm t, từ đó suy ra tọa độ điểm H.
b) A' đối xứng với A qua đường thẳng d suy ra H là trung điểm của AA', với H là hình chiếu vuông góc của A trên . Từ đó tìm tọa độ điểm A'.
Lời giải:
a) Đường thẳng có vectơ chỉ phương . nên .
Điểm là hình chiếu vuông góc của lên khi và chỉ khi .
Ta có nên:
⊥ ⇔ = 0.
⇔
⇔ .
⇔ .
b) Gọi là điểm đối xứng của qua và là hình chiếu vuông góc của lên thì là trung điểm của .
a) Tìm tọa độ điểm là hình chiếu vuông góc của điểm trên mặt phẳng .
b) Tìm tọa độ điểm đối xứng với qua mặt phẳng .
c) Tính khoảng cách từ điểm đến mặt phẳng .
Phương pháp giải:
a) Phương pháp tìm hình chiếu của điểm M trên mặt phẳng (P).
Bước 1: Viết phương trình đường thẳng d đi qua M và vuông góc với (P).
Bước 2: Gọi , tìm tọa độ điểm H. H chính là hình chiếu vuông góc của M trên mặt phẳng (P).
b) Điểm M' đối xứng với M qua mặt phẳng (P) nhận H làm trung điểm, với H là hình chiếu vuông góc của M trên mặt phẳng (P). Tìm tọa độ điểm M'.
c) Sử dụng công thức tính khoảng cách từ 1 điểm đến mặt phẳng :
Lời giải:
a) Xét đường thẳng qua và .
Vectơ là vectơ pháp tuyến của nên là vectơ chỉ phương của .
Phương trình tham số của đường thẳng có dạng: .
Gọi , , vì nên ta có:
b) Gọi là điểm đối xứng của qua mặt phẳng , thì hình chiếu vuông góc của xuống chính là trung điểm của .
Ta có:
c) Tính khoảng cách từ điểm đến mặt phẳng
Cách 1:
Cách 2: Khoảng cách từ M đến (α) chính là khoảng cách MH: = .
Chứng minh và chéo nhau.
Phương pháp giải:
Xác định các VTCP của và ,chứng minh 2 vector đó không cùng phương.
Sử dụng điều kiện để hai đường thẳng chéo nhau: với lần lượt là VTCP của và .
Lời giải:
Đường thẳng qua điểm và có vec tơ chỉ phương .
Đường thẳng qua điểm và có vectơ chỉ phương .
Dễ thấy không cùng phương, do đó d và d' hoặc cắt nhau, hoặc chéo nhau.
Xét
.
Ta có :
Vậy và chéo nhau.
Cách khác:
Có hai VTCP của hai đường thẳng không cùng phương (cmt)
Xét hệ:
Vậy hai đường thẳng chéo nhau.
Cho hình lập phương có cạnh bằng . Tính khoảng cách từ đỉnh đến các mặt phẳng và .
Phương pháp giải:
+) Gắn hệ trục tọa độ sao cho
+) Tìm tọa độ các đỉnh còn lại của hình lập phương.
+) Viết phương trình các mặt phẳng và .
+) Sử dụng công thức tính khoảng cách từ 1 điểm đến một mặt phẳng tính khoảng cách từ đỉnh đến các mặt phẳng và .
Lời giải:
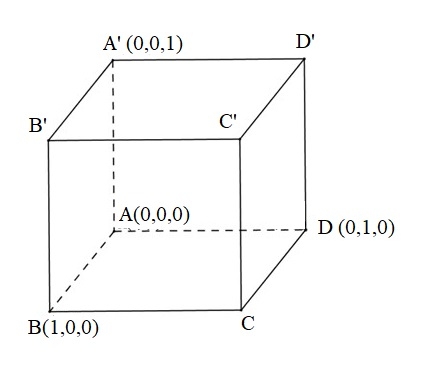
Chọn hệ trục tọa độ sao cho
Khi đó .
Phương trình mặt phẳng có dạng: .
;
Mặt phẳng qua điểm và nhận hay làm vectơ pháp tuyến
Phương trình mặt phẳng có dạng:
Vậy:
1. Phương trình tham số
Đường thẳng qua điểm có vectơ chỉ phương (a1 ; a2 ; a3) có phương trình tham số dạng:
, t ∈ R là tham số.
Nếu đều khác không, ta viết phương trình trên ở dạng chính tắc:
2. Vị trí tương đối
Cho đường thẳng qua điểm và có vec tơ chỉ phương , đường thẳng qua điểm và có vec tơ chỉ phương .
* và chéo nhau và không nằm trong cùng một mặt phẳng ⇔ .
* và song song ⇔ .
* trùng với ⇔ , , là ba vectơ cùng phương.
* cắt ⇔ không cùng phương và .
Sơ đồ tư duy về phương trình đường thẳng trong không gian
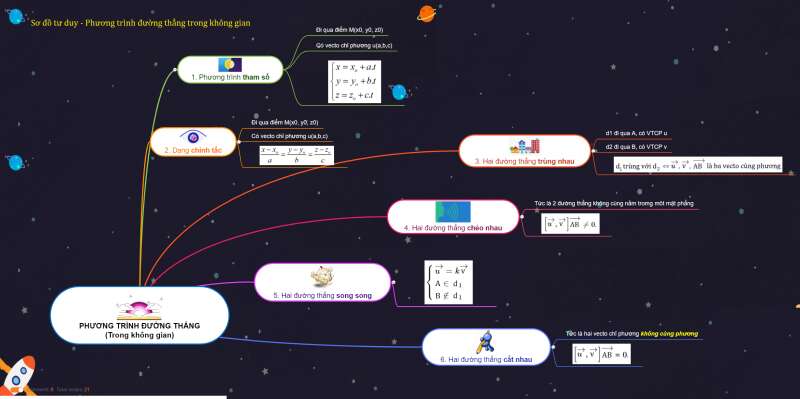
- Phương trình tham số của đường thẳng:
ở đó là điểm thuộc dường thẳng và là VTCP của đường thẳng.
- Phương trình chính tắc của đường thẳng:
ở đó là điểm thuộc dường thẳng và là VTCP của đường thẳng.
- Đường thẳng có
- Đường thẳng
2. Một số dạng toán thường gặp
Dạng 1: Nhận biết các yếu tố trong phương trình đường thẳng.
Phương pháp:
Sử dụng các lý thuyết về phương trình đường thẳng để tìm điểm đi qua, VTCP,…
Dạng 2: Chuyển đổi các dạng phương trình chính tắc và tham số.
Phương pháp:
- Bước 1: Tìm điểm đi qua và VTCP của đường thẳng trong phương trình đã cho.
- Bước 2: Viết phương trình dạng chính tắc, tham số dựa vào hai yếu tố vừa xác định được ở trên.
Đường thẳng đi qua điểm và có VTCP thì có:
+ Phương trình chính tắc:
+ Phương trình tham số:
Dạng 3: Viết phương trình đường thẳng.
Phương pháp chung:
- Bước 1: Tìm điểm đi qua .
- Bước 2: Tìm VTCP của đường thẳng.
- Bước 3: Viết phương trình tham số hoặc chính tắc của đường thẳng biết hai yếu tố trên.
+) Đi qua hai điểm.
Đường thẳng đi qua và nhận làm VTCP.
+) Đi qua một điểm và song song với một đường thẳng.
Đường thẳng qua và song song với thì có VTCP

+) Đi qua một điểm và vuông góc với hai đường thẳng.
Đường thẳng đi qua điểm và vuông góc với hai đường thẳng thì có VTCP
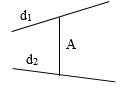
a) Khoảng cách từ điểm đến đường thẳng
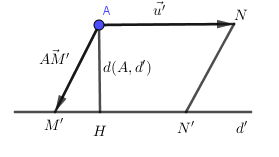
b) Khoảng cách giữa hai đường thẳng
c) Góc giữa hai đường thẳng có các VTCP lần lượt là:

