Giải Toán 12 Bài 4: Đường tiệm cận

50 lượt xem

Bài trước

Bài sau

Chúng tôi giới thiệu Giải bài tập Toán lớp 12 Bài 4: Đường tiệm cận chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Đường tiệm cận lớp 12.

Bài giảng Toán học 12 Bài 4: Đường tiệm cận

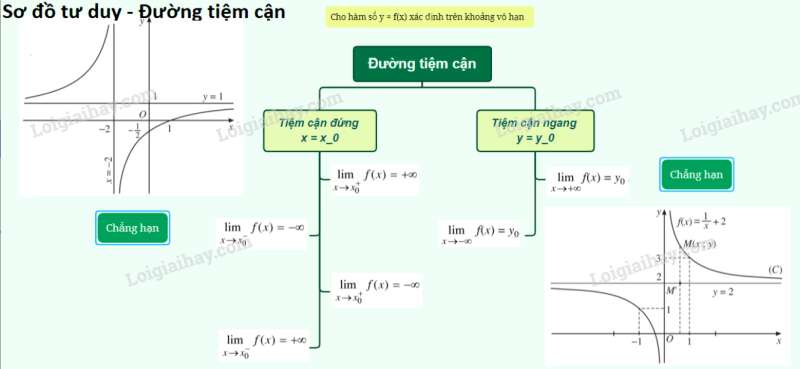
Giải bài tập Toán lớp 12 Bài 4: Đường tiệm cận

Trả lời câu hỏi giữa bài

Trả lời câu hỏi 1 trang 27 SGK Giải tích 12: Cho hàm số: $y = \frac{2 - x}{x - 1}$ (H.16) có đồ thị (C).

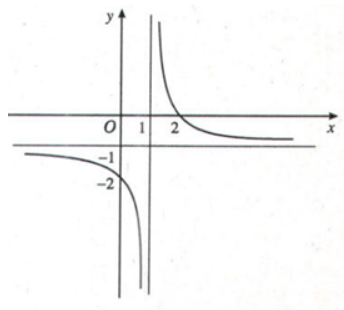
Nêu nhận xét về khoảng cách từ điểm $M (x; y) \in (C)$ tới đường thẳng $y = - 1$ khi $| x | \to + \infty$

Lời giải:

Khoảng cách từ điểm $M (x; y) \in (C)$ tới đường thẳng $y = - 1$ khi $| x | \to + \infty$ dần tiến về 0.

Trả lời câu hỏi 2 trang 29 SGK Giải tích 12: Tính

lim_{x \to 0} (\frac{1}{x} + 2)

và nêu nhận xét về khoảng cách

M H

khi

x \to 0

(H.17)

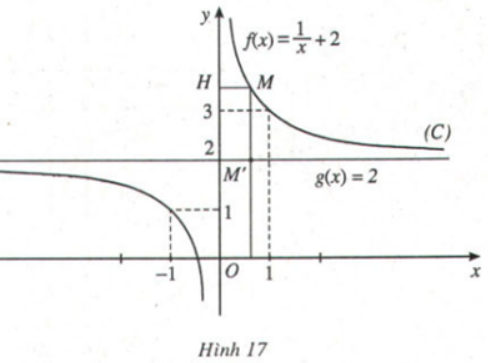
Lời giải:

$\begin{aligned} lim_{x \to 0^{+}} (\frac{1}{x} + 2) = + \infty \\ lim_{x \to 0^{-}} (\frac{1}{x} + 2) = - \infty \end{aligned}$

Khi $x$ dần đến $0$ thì độ dài đoạn $M H$ dần tiến đến $0$ .

Câu hỏi và bài tập (trang 30 SGK Giải tích 12)

Bài 1 trang 30 SGK Giải tích 12: Tìm các tiệm cận của đồ thị hàm số:

a) $y = \frac{x}{2 - x}$ .

b) $y = \frac{- x + 7}{x + 1}$ .

c) $y = \frac{2 x - 5}{5 x - 2}$ .

d) $y = \frac{7}{x} - 1$ .

Phương pháp giải:

- Tính $lim f (x)$ khi $x \to \pm \infty$ . Nếu ít nhất $lim_{x \to + \infty} f (x) = y_{0}$ hoặc $lim_{x \to - \infty} f (x) = y_{0}$ thì ta KL $y = y_{0}$ là đường tiệm cận ngang

- Tính $lim f (x)$ khi $x \to {x_{0}}^{+}$ ; $x \to {x_{0}}^{-}$

nếu ít nhất một trong các điều kiện sau được thỏa mãn:

$\begin{array}{l} lim_{x \to x_{0}^{+}} f (x) = + \infty; lim_{x \to x_{0}^{-}} f (x) = - \infty \\ lim_{x \to x_{0}^{+}} f (x) = - \infty; lim_{x \to x_{0}^{-}} f (x) = + \infty \end{array}$

Ta KL: Đường thẳng $x = x_{0}$ là đường tiệm cận đứng của đồ thị hàm số $y = f (x)$

Lời giải:

Ta có: $lim_{x \to 2^{-}} \frac{x}{2 - x} = + \infty;$ $lim_{x \to 2^{+}} \frac{x}{2 - x} = - \infty$ nên đường thẳng $x = 2$ là tiệm cận đứng của đồ thị hàm số.

Ta có: $lim_{x \to + \infty} \frac{x}{2 - x} = - 1;$ $lim_{x \to - \infty} \frac{x}{2 - x} = - 1$ nên đường thẳng $y = - 1$ là tiệm cận ngang của đồ thị hàm số.

Ta có: $lim_{x \to {(- 1)}^{+}} \frac{- x + 7}{x + 1} = + \infty;$ $lim_{x \to {(- 1)}^{-}} \frac{- x + 7}{x + 1} = - \infty$ nên $x = - 1$ là tiệm cận đứng của đồ thị hàm số.

Ta có: $lim_{x \to + \infty} \frac{- x + 7}{x + 1} = - 1;$ $lim_{x \to - \infty} \frac{- x + 7}{x + 1} = - 1$ nên đường thẳng $y = - 1$ là tiệm cận ngang của đồ thị hàm số.

Ta có: $lim_{x \to {(\frac{2}{5})}^{+}} \frac{2 x - 5}{5 x - 2} = - \infty;$ $lim_{x \to {(\frac{2}{5})}^{-}} \frac{2 x - 5}{5 x - 2} = + \infty$ nên đường thẳng $x = \frac{2}{5}$ là tiệm cận đứng của đồ thị hàm số.

Ta có: $lim_{x \to - \infty} \frac{2 x - 5}{5 x - 2} = \frac{2}{5};$ $lim_{x \to + \infty} \frac{2 x - 5}{5 x - 2} = \frac{2}{5}$ nên đồ thị hàm số nhận đường thẳng $y = \frac{2}{5}$ làm tiệm cận ngang.

Ta có: $lim_{x \to 0^{+}} (\frac{7}{x} - 1) = + \infty;$ $lim_{x \to 0^{-}} (\frac{7}{x} - 1) = - \infty$ nên đường thẳng $x = 0$ là tiệm cận đứng của đồ thị hàm số.

Ta có: $lim_{x \to - \infty} (\frac{7}{x} - 1) = - 1;$ $lim_{x \to + \infty} (\frac{7}{x} - 1) = - 1$

( vì $lim_{x \to \infty} \frac{1}{x} = 0$ )

Do đó đường thẳng $y = - 1$ là tiệm cận ngang của đồ thị hàm số.

Bài 2 trang 30 SGK Giải tích 12: Tìm các tiệm cận đứng và tiệm cận ngang của đồ thị hàm số:

a) $y = \frac{2 - x}{9 - x^{2}}$

b) $y = \frac{x^{2} + x + 1}{3 - 2 x - 5 x^{2}}$

c) $y = \frac{x^{2} - 3 x + 2}{x + 1}$

d) $y = \frac{\sqrt{x} + 1}{\sqrt{x} - 1}$

Phương pháp giải:

- Tìm tiệm cận ngang:

+ Tính $lim_{x \to + \infty} f (x); lim_{x \to - \infty} f (x)$

+ Nếu $lim_{x \to + \infty} f (x) = y_{0}$ hoặc $lim_{x \to - \infty} f (x) = y_{0}$ , ta kết luận: $y = y_{0}$ là đường tiệm cận ngang của đồ thị hàm số $y = f (x)$

- Tìm tiệm cận đứng:

+ Tìm TXĐ

+ Tính $lim f (x)$ khi $x \to {x_{0}}^{+}$ và $x \to {x_{0}}^{-}$ với $x_{0}$ là giá trị làm hàm số không xác định.

Nếu $\begin{array}{l} lim_{x \to x_{0}^{+}} f (x) = + \infty; lim_{x \to x_{0}^{-}} f (x) = - \infty \\ lim_{x \to x_{0}^{+}} f (x) = - \infty; lim_{x \to x_{0}^{-}} f (x) = + \infty \end{array}$

Ta kết luận: Đường thẳng $x = x_{0}$ là đường tiệm cận đứng của đồ thị hàm số $y = f (x)$

Lời giải:

TXĐ: $D = R ∖ {\pm 3}$

$lim_{x \to (- 3)^{+}} \frac{2 - x}{9 - x^{2}} = + \infty$ nên đường thẳng $x = - 3$ là tiệm cận đứng của đồ thị hàm số.

$lim_{x \to 3^{+}} \frac{2 - x}{9 - x^{2}} = + \infty$ nên đường thẳng $x = 3$ là tiệm cận đứng của đồ thị hàm số.

$lim_{x \to + \infty} \frac{2 - x}{9 - x^{2}} = 0$ nên đường thẳng: $y = 0$ là tiệm cận ngang của đồ thị hàm số.

TXĐ: $D = R ∖ {- 1; \frac{3}{5}}$

$\begin{array}{l} lim_{x \to {(- 1)}^{+}} \frac{x^{2} + x + 1}{3 - 2 x - 5 x^{2}} = + \infty; \\ lim_{x \to {(- 1)}^{-}} \frac{x^{2} + x + 1}{3 - 2 x - 5 x^{2}} = - \infty \\ lim_{x \to {(\frac{3}{5})}^{+}} \frac{x^{2} + x + 1}{3 - 2 x - 5 x^{2}} = - \infty; \\ lim_{x \to {(\frac{3}{5})}^{-}} \frac{x^{2} + x + 1}{3 - 2 x - 5 x^{2}} = + \infty \end{array}$

Nên đồ thị hàm số có hai tiệm cận đứng là các đường thẳng: $x = - 1; x = \frac{3}{5}$ .

Vì: $lim_{x \to - \infty} \frac{x^{2} + x + 1}{3 - 2 x - 5 x^{2}} = - \frac{1}{5};$ $lim_{x \to + \infty} \frac{x^{2} + x + 1}{3 - 2 x - 5 x^{2}} = - \frac{1}{5}$

Nên đồ thị hàm số có tiệm cận ngang là đường thẳng $y = - \frac{1}{5}$ .

TXĐ: $D = R ∖ {- 1}$

$lim_{x \to {(- 1)}^{-}} \frac{x^{2} - 3 x + 2}{x + 1} = - \infty;$ $lim_{x \to {(- 1)}^{+}} \frac{x^{2} - 3 x + 2}{x + 1} = + \infty$ nên đường thẳng $x = - 1$ là một tiệm cận đứng của đồ thị hàm số.

$lim_{x \to - \infty} \frac{x^{2} - 3 x + 2}{x + 1}$ $= lim_{x \to - \infty} \frac{x^{2} (1 - \frac{3}{x} + \frac{2}{x^{2}})}{x (1 + \frac{1}{x})} = - \infty$ và $lim_{x \to + \infty} \frac{x^{2} - 3 x + 2}{x + 1} = + \infty$ nên đồ thị hàm số không có tiệm cận ngang.

Hàm số xác định khi: ${\begin{matrix} x \geq 0 \\ \sqrt{x} - 1 \neq 0 \end{matrix} \Leftrightarrow {\begin{matrix} x \geq 0 \\ x \neq 1 \end{matrix}$

$\Rightarrow D = [0; + \infty) ∖ {1}$

Vì $lim_{x \to 1^{-}} \frac{\sqrt{x} + 1}{\sqrt{x} - 1} = - \infty$ nên đường thẳng $x = 1$ là một tiệm cận đứng của đồ thị hàm số.

Vì $lim_{x \to + \infty} \frac{\sqrt{x} + 1}{\sqrt{x} - 1}$ $= lim_{x \to + \infty} \frac{\sqrt{x} (1 + \frac{1}{\sqrt{x}})}{\sqrt{x} (1 - \frac{1}{\sqrt{x}})} = 1$ nên đường thẳng $y = 1$ là một tiệm cận ngang của đồ thị hàm số.

Chú ý: Có thể sử dụng MTCT để tính toán các giới hạn.

Lý thuyết Bài 4: Đường tiệm cận

Cho hàm số $y = f (x)$ có đồ thị $(C)$ .

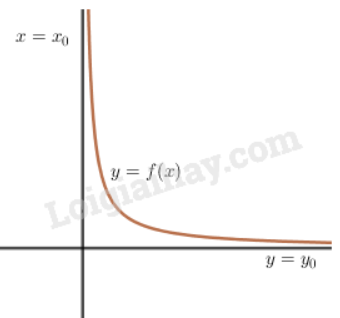
1. Tiệm cận đứng

Đường thẳng $x = a$ là đường tiệm cận đứng của $(C)$ nếu ít nhất một trong bốn điều kiện sau được thoả mãn:

$\begin{aligned} lim_{x \to a^{+}} f (x) = + \infty \\ lim_{x \to a^{+}} f (x) = - \infty \\ lim_{x \to a^{-}} f (x) = + \infty \\ lim_{x \to a^{-}} f (x) = - \infty \end{aligned}$

2. Tiệm cận ngang

Đường thẳng $y = b$ là tiệm cận ngang của $(C)$ nếu ít nhất một trong các điều kiện sau được thỏa mãn:

$\begin{aligned} lim_{x \to + \infty} f (x) = b \\ lim_{x \to - \infty} f (x) = b \end{aligned}$

Chú ý

- Đồ thị hàm đa thức không có tiệm cận đứng và tiệm cận ngang, do đó trong các bài toán khảo sát và vẽ đồ thị hàm đa thức, ta không cần tìm các tiệm cận này.

3. Tiệm cận xiên

Đường thẳng $y = a x + b (a \neq 0)$ được gọi là tiệm cận xiên của đồ thị hàm số $y = f (x)$ nếu nó thỏa mãn một trong 2 điều kiện sau: $[\begin{array}{l} lim_{x \to + \infty} [f (x) - (a x + b)] = 0 \\ lim_{x \to - \infty} [f (x) - (a x + b)] = 0 \end{array}$ , trong đó:

${\begin{cases} a = lim_{x \to + \infty} \frac{f (x)}{x} \\ b = lim_{x \to + \infty} [f (x) - a x] \end{cases}$ hoặc ${\begin{cases} a = lim_{x \to - \infty} \frac{f (x)}{x} \\ b = lim_{x \to - \infty} [f (x) - a x] \end{cases}$

Chỉ có khái niệm “Tiệm cận của đồ thị hàm số”, KHÔNG có “Tiệm cận của hàm số”.

Sơ đồ tư duy về đường tiệm cận

Xem thêm các chương trình khác:

Bài trước

Bài sau

Giải SGK, SBT, Chuyên đề Toán Học Lớp 12

Giải Toán 12 Bài 4: Đường tiệm cận

Xem thêm các chương trình khác: