Giải Toán 12 Bài 2: Hàm số lũy thừa

79 lượt xem

Bài trước

Bài sau

Chúng tôi giới thiệu Giải bài tập Toán lớp 12 Bài 2: Hàm số lũy thừa chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Hàm số lũy thừa lớp 12.

Bài giảng Toán học 12 Bài 2: Hàm số lũy thừa

Giải bài tập Toán lớp 12 Bài 2: Hàm số lũy thừa

Trả lời câu hỏi giữa bài

Trả lời câu hỏi 1 trang 57 SGK Giải tích 12: Vẽ trên cùng một hệ trục tọa độ đồ thị của các hàm số sau và nêu nhận xét về tập xác định của chúng:

$y = x^{2}; y = x^{\frac{1}{2}}; y = x^{- 1}$

Lời giải:

Đồ thị của hàm số $y = x^{2}$ : đường màu đỏ.

Đồ thị của hàm số $y = x^{\frac{1}{2}}$ : đường màu xanh.

Đồ thị của hàm số $y = x^{- 1}$ : đường màu tím.

Ta có:

Tập xác định của hàm số $y = x^{2}$ là $R .$

Tập xác định của hàm số $y = x^{\frac{1}{2}}$ là $(0, + \infty)$ .

Tập xác định của hàm số $y = x^{- 1}$ là $R ∖ {0}$ .

Trả lời câu hỏi 2 trang 57 SGK Giải tích 12: Tính đạo hàm của các hàm số:

y = x^{\frac{- 2}{3}}; y = x^{π}; y = x^{\sqrt{2}}

Phương pháp giải:

Sử dụng công thức đạo hàm

{(x^{α})}^{'} = α x^{α - 1}

Lời giải:

$\begin{aligned} y^{'} = (x^{\frac{- 2}{3}})^{'} = - \frac{2}{3} . x^{(\frac{- 2}{3} - 1)} \\ = \frac{- 2}{3} . x^{\frac{- 5}{3}} \\ y^{'} = (x^{π})^{'} = π . x^{π - 1} \\ y^{'} = (x^{\sqrt{2}})^{'} = \sqrt{2} . x^{\sqrt{2} - 1} \end{aligned}$

Trả lời câu hỏi 3 trang 58 SGK Giải tích 12: Tính đạo hàm của hàm số:

y = (3 x^{2} - 1)^{(- \sqrt{2})}

Phương pháp giải:

Sử dụng công thức đạo hàm

{(u^{α})}^{'} = α u^{α - 1} . u^{'}

Lời giải:

$\begin{aligned} y^{'} = {[{(3 x^{2} - 1)}^{(- \sqrt{2})}]}^{'} \\ = - \sqrt{2} (3 x^{2} - 1)^{(- \sqrt{2} - 1)} . (3 x^{2} - 1)^{'} \\ = - \sqrt{2} (3 x^{2} - 1)^{(- \sqrt{2} - 1)} .6 x \\ = - 6 \sqrt{2} x (3 x^{2} - 1)^{(- \sqrt{2} - 1)} \end{aligned}$

Câu hỏi và bài tập (trang 60, 61 SGK Giải tích 12)

Bài 1 trang 60 SGK Giải tích 12: Tìm tập xác định của các hàm số:

a) $y = {(1 - x)}^{\frac{- 1}{3}}$ ;

b) y=

{(2 - x^{2})}^{\frac{3}{5}}

;

y = {(x^{2} - 1)}^{- 2}

;

y = {(x^{2} - x - 2)}^{\sqrt{2}}

Phương pháp giải:

Tập xác định của hàm số lũy thừa $y = x^{n}$ tùy thuộc vào giá trị của $n$ :

Với $n$ là số nguyên dương, tập xác định là $R .$

Với $n$ là số nguyên âm hoặc bằng 0, tập xác định là $R ∖ {0}$ .

Với $n$ không nguyên, tập xác định là $(0; + \infty)$

Lời giải:

$y = {(1 - x)}^{\frac{- 1}{3}}$ có $n = - \frac{1}{3} \notin Z$ xác định khi và chỉ khi:

$1 - x > 0 \Leftrightarrow x < 1$ .

Vậy $D = (- \infty; 1)$ .

$y = {(2 - x^{2})}^{\frac{3}{5}}$ có $n = \frac{3}{5} \notin Z$ xác định khi và chỉ khi:

$2 - x^{2} > 0 \Leftrightarrow x^{2} < 2$

$\Leftrightarrow - \sqrt{2} < x <$ $\sqrt{2}$ .

Vậy $D = (- \sqrt{2}; \sqrt{2})$ .

$y = {(x^{2} - 1)}^{- 2}$ có $n = - 2 \in Z^{-}$ xác định khi và chỉ khi:

$x^{2} - 1 \neq 0 \Leftrightarrow x \neq \pm 1$ .

Vậy $D = R ∖ {- 1; 1}$ .

$y = {(x^{2} - x - 2)}^{\sqrt{2}}$ có $n = \sqrt{2} \notin Z$ xác định khi và chỉ khi:

$x^{2} - x - 2 > 0 \Leftrightarrow [\begin{array}{l} x > 2 \\ x < - 1 \end{array}$

Vậy $D = (- \infty; - 1) \cup (2; + \infty)$ .

Bài 2 trang 61 SGK Giải tích 12: Tìm các đạo hàm của các hàm số:

a) $y = {(2 x^{2} - x + 1)}^{\frac{1}{3}}$ ;

y = {(4 - x - x^{2})}^{\frac{1}{4}}

;

y = {(3 x + 1)}^{\frac{π}{2}}

;

y = {(5 - x)}^{\sqrt{3}}

Phương pháp giải:

Sử dụng công thức tính đạo hàm của hàm hợp đối với hàm số lũy thừa: ${(u^{α})}^{'} = α . u^{α - 1} . u^{'} .$

Lời giải:

$y^{^{'}} = \frac{1}{3} {(2 x^{2} - x + 1)}^{^{'}} {(2 x^{2} - x + 1)}^{\frac{1}{3} - 1}$

$= \frac{1}{3} (4 x - 1) . {(2 x^{2} - x + 1)}^{- \frac{2}{3}}$

$y^{^{'}} = \frac{1}{4} {(4 - x - x^{2})}^{^{'}} {(4 - x - x^{2})}^{\frac{1}{4} - 1}$

= $\frac{1}{4} (- 2 x - 1) {(4 - x - x^{2})}^{\frac{- 3}{4}}$ .

$y^{^{'}}$ = $\frac{π}{2} {(3 x + 1)}^{^{'}} {(3 x + 1)}^{\frac{π}{2} - 1}$

= $\frac{3 π}{2} {(3 x + 1)}^{\frac{π}{2} - 1}$ .

$y^{^{'}}$ = $\sqrt{3} {(5 - x)}^{^{'}} {(5 - x)}^{\sqrt{3} - 1}$

= $- \sqrt{3} {(5 - x)}^{\sqrt{3} - 1}$ .

Bài 3 trang 61 SGK Giải tích 12: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số:

a) $y = x^{\frac{4}{3}}$ ;

y = x^{- 3}

Phương pháp giải:

Các bước khảo sát sự biến thiên và vẽ đồ thị hàm số:

Bước 1: Tìm tập xác định của hàm số.

Bước 2: Tính y', tìm các điểm mà tại đó có y' bằng 0 hoặc không xác định, xét dấu y' và suy ra các chiều biến thiên của hàm số. Tìm các cực trị, các giới hạn tại vô cực và các đường tiệm cận để lập BBT của đồ thị hàm số.

Bước 3: Dựa vào bảng biến thiên và các yếu tố xác định ở trên để vẽ đồ thị hàm số.

Lời giải:

Hàm số $y = x^{\frac{4}{3}}$

*) Tập xác định: $D = (0; + \infty)$ .

+) Sự biến thiên:

Ta có: $y^{'} = \frac{4}{3} . x^{\frac{1}{3}} > 0, \forall x > 0$

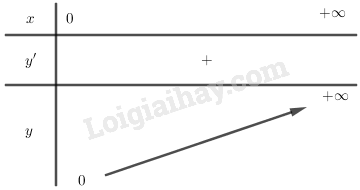
- Hàm số đồng biến trên khoảng $(0; + \infty)$

- Giới hạn đặc biệt: $lim_{x \to + \infty} y = + \infty$ .

- Đồ thị hàm số không có tiệm cận.

- Bảng biến thiên

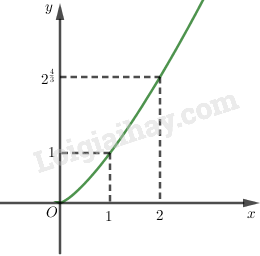
*) Đồ thị: Đồ thị hàm số qua $(1; 1)$ , $(2; \sqrt[3]{2^{4}})$ .

Hàm số $y = x^{- 3}$

*) Tập xác định: $D = ℝ ∖ {0}$ .

*) Sự biến thiên:

Ta có: $y^{'} = - 3 x^{- 4} < 0, \forall x \in D$

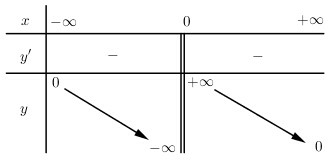
- Hàm nghịch biến trong khoảng $(- \infty; 0)$ và $(0; + \infty)$ .

- Giới hạn đặc biệt:

$\begin{aligned} lim_{x \to 0^{+}} y = + \infty \\ lim_{x \to 0^{-}} y = - \infty \\ lim_{x \to \pm \infty} y = 0 \end{aligned}$

- Đồ thị hàm số nhận trục tung làm tiệm cận đứng, trục hoành làm tiệm cận ngang.

- Bảng biến thiên

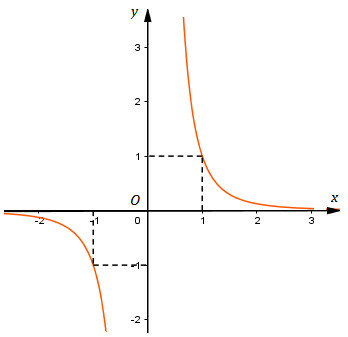
*) Đồ thị:

Đồ thị qua $(- 1; - 1)$ , $(1; 1)$ , $(2; \frac{1}{8})$ , $(- 2; \frac{- 1}{8})$ .

Hàm số đã cho là hàm số lẻ nên đồ thị có tâm đối xứng là gốc tọa độ.

Bài 4 trang 61 SGK Giải tích 12: Hãy so sánh các số sau với

1

a) ${(4, 1)}^{2, 7}$ ;

{(0, 2)}^{0, 3}

;

{(0, 7)}^{3, 2}

;

{(\sqrt{3})}^{0, 4}

Phương pháp giải:

Sử dụng phương pháp so sánh hai lũy thừa cùng cơ số:

$a^{f (x)} < a^{g (x)} \Leftrightarrow [\begin{array}{l} {\begin{cases} a > 1 \\ f (x) < g (x) \end{cases} \\ {\begin{cases} 0 < a < 1 \\ f (x) > g (x) \end{cases} \end{array}$

Lời giải:

Ta có: $1 = {(4, 1)}^{0}$

Vì ${\begin{matrix} 4, 1 > 1 \\ 2, 7 > 0 \end{matrix} \Rightarrow {(4, 1)}^{2, 7} > {(4, 1)}^{0} = 1$

Cách khác.

Ta có: $2, 7 > 0$ nên hàm $y = x^{2, 7}$ luôn đồng biến trên $(0; + \infty) .$

Vì $4, 1 > 1 \Rightarrow {(4, 1)}^{2, 7} > 1^{2, 7} = 1.$

Ta có: $1 = {(0, 2)}^{0}$

Vì ${\begin{matrix} 0, 2 < 1 \\ 0, 3 > 0 \end{matrix} \Rightarrow {(0, 2)}^{0, 3} < {(0, 2)}^{0} = 1$

Cách khác:

Ta có : $0, 3 > 0$ nên hàm số $y = x^{0, 3}$ đồng biến trên $(0; + \infty) .$

Vì $0, 2 < 1 \Rightarrow 0, 2^{0, 3} < 1^{0, 3} = 1.$

Ta có: $1 = {(0, 7)}^{0}$

Vì ${\begin{matrix} 0, 7 < 1 \\ 3, 2 > 0 \end{matrix} \Rightarrow {(0, 7)}^{3, 2} < {(0, 7)}^{0} = 1$

Cách khác:

Ta có: $3, 2 > 0$ nên hàm số $y = x^{3, 2}$ đồng biến trên $(0; + \infty)$

Vì $0, 7 < 1 \Rightarrow 0, 7^{3, 2} < 1^{3, 2} = 1$

Ta có: $1 = {(\sqrt{3})}^{0}$

Vì ${\begin{matrix} \sqrt{3} > 1 \\ 0, 4 > 0 \end{matrix} \Rightarrow {(\sqrt{3})}^{0, 4} > {(\sqrt{3})}^{0} = 1$

Cách khác:

Ta có: $0, 4 > 0$ nên hàm số $y = x^{0, 4}$ đồng biến trên $(0; + \infty)$

Vì $\sqrt{3} > 1 \Rightarrow {(\sqrt{3})}^{0, 4} > 1^{0, 4} = 1.$

Bài 5 trang 61 SGK Giải tích 12: Hãy so sánh các cặp số sau:

a) ${(3, 1)}^{7, 2}$ và ${(4, 3)}^{7, 2}$ ;

{(\frac{10}{11})}^{2, 3}

và

{(\frac{12}{11})}^{2, 3}

;

{(0, 3)}^{0, 3}

và

{(0, 2)}^{0, 3}

Phương pháp giải:

Sử dụng phương pháp so sánh hai lũy thừa cùng số mũ:

Nếu $α > 0$ thì $a > b \Leftrightarrow a^{α} > b^{α}$

Nếu $α < 0$ thì $a > b \Leftrightarrow a^{α} < b^{α}$

Lời giải:

Vì $7, 2 > 0$ và $3, 1 < 4, 3$ suy ra ${(3, 1)}^{7, 2}$ < ${(4, 3)}^{7, 2}$ .

Vì $2, 3 > 0$ và $\frac{10}{11}$ < $\frac{12}{11}$ suy ra ${(\frac{10}{11})}^{2, 3}$ < ${(\frac{12}{11})}^{2, 3}$ .

Vì $0, 3 > 0$ và $0, 3 > 0, 2$ suy ra ${(0, 3)}^{0, 3}$ > ${(0, 2)}^{0, 3}$ .

Lý thuyết Bài 2: Hàm số lũy thừa

1. Khái niệm hàm số lũy thừa

Hàm số lũy thừa là các hàm số dạng $y = x^{α} (α \in R)$ . Các hàm số lũy thừa có tập xác định khác nhau, tùy theo $α$ :

- Nếu $α$ nguyên dương thì tập các định là $R$ .

- Nếu $α$ nguyên âm hoặc $α = 0$ thì tập các định là $R ∖ {0}$ .

- Nếu $α$ không nguyên thì tập các định là $(0; + \infty)$ .

Chú ý: Hàm số $y = \sqrt{x}$ có tập xác định là $[0; + \infty)$ , hàm số $y = \sqrt[3]{x}$ có tập xác định $R$ , trong khi đó các hàm $y = x^{\frac{1}{2}}, y = x^{\frac{1}{3}}$ đều có tập xác định $(0; + \infty)$ . Vì vậy $y = \sqrt{x}$ và $y = x^{\frac{1}{2}}$ ( hay $y = \sqrt[3]{x}$ và $y = x^{\frac{1}{3}}$ ) là những hàm số khác nhau.

2. Đạo hàm của hàm số lũy thừa với số mũ tổng quát

- Hàm số $y = x^{α}$ có đạo hàm tai mọi $x \in (0; + \infty)$ và $y^{'} = {(x^{α})}^{'} = α x^{α - 1}$

- Nếu hàm số $u = u (x)$ nhận giá trị dương và có đạo hàm trong khoảng $J$ thì hàm số $y = u^{α} (x)$ cũng có đạo hàm trên $J$ và $y^{'} = {[u^{α} (x)]}^{'} = α u^{α - 1} (x) u^{'} (x)$

3. Đạo hàm của hàm số lũy thừa với số mũ nguyên dương

Trong trường hợp số mũ nguyên dương, hàm số lũy thừa $y = x^{n}$ có tập xác định là $R$ và có đạo hàm trên toàn trục số. Công thức tính đạo hàm số lũy thừa tổng quát được mở rộng thành $\forall x \in R, {(x^{n})}^{'} = n x^{n - 1}$ và $\forall x \in J, {[u^{n} (x)]}^{'} = n u^{n - 1} (x) u^{'} (x)$ nếu $u = u (x)$ có đạo hàm trong khoảng $J$ .

4. Đạo hàm của hàm số lũy thừa với số mũ nguyên âm

Nếu số mũ là số nguyên âm thì hàm số lũy thừa $y = x^{n}$ có tập xác định là $R ∖ {0}$ và có đạo hàm tại mọi $x$ khác $0$ , công thức đạo hàm hàm số lũy thừa tổng quát được mở rộng thành $\forall x \neq 0, {(x^{n})}^{'} = n x^{n - 1}$ và $\forall x \in J, {[u^{n} (x)]}^{'} = n u^{n - 1} (x) u^{'} (x)$

nếu $u = u (x) \neq 0$ có đạo hàm trong khoảng $J$ .

5. Đạo hàm của căn thức

Hàm số $y = \sqrt[n]{x}$ có thể xem là mở rộng của hàm lũy thừa $y = x^{\frac{1}{n}}$ (tập xác định của $y = \sqrt[n]{x}$ chứa tập xác định của $y = x^{\frac{1}{n}}$ và trên tập xác định của $y = x^{\frac{1}{n}}$ thì hai hàm số trùng nhau).

Khi $n$ lẻ thì hàm số $y = \sqrt[n]{x}$ có tập xác định $R$ . Trên khoảng $(0; + \infty)$ ta có $y = \sqrt[n]{x} = x^{\frac{1}{n}}$ và ${(x^{\frac{1}{n}})}^{'} = \frac{1}{n} x^{\frac{1}{n} - 1}$ , do đó ${(\sqrt[n]{x})}^{'} = \frac{1}{n \sqrt[n]{x^{n - 1}}}$ .

Công thức này còn đúng cả với $x < 0$ và hàm số $y = \sqrt[n]{x}$ không có đạo hàm tại $x = 0$ .

Khi $n$ chẵn hàm $y = \sqrt[n]{x}$ có tập xác định là $[0; + \infty)$ , không có đạo hàm tại $x = 0$ và có đạo hàm tại mọi $x > 0$ tính theo công thức:

${(\sqrt[n]{x})}^{'} = {(\sqrt[n]{x})}^{'} = \frac{1}{n \sqrt[n]{x^{n - 1}}}$

Tóm lại, ta có ${(\sqrt[n]{x})}^{'} = {(\sqrt[n]{x})}^{'} = \frac{1}{n \sqrt[n]{x^{n - 1}}}$ đúng với mọi $x$ làm cho hai vế có nghĩa.

Sử dụng quy tắc đạo hàm hàm hợp ta suy ra: Nếu $u = u (x)$ là hàm có đạo hàm trên khoảng $J$ và thỏa mãn điều kiện $u (x) > 0, \forall x \in J$ khi $n$ chẵn, $u (x) \neq 0, \forall x \in J$ khi $n$ lẻ thì

$\forall x \in J, {(\sqrt[n]{u (x)})}^{'} = \frac{u^{'} (x)}{n \sqrt[n]{u^{n - 1} (x)}}$

6. Đồ thị hàm số $y = x^{α}$ trên khoảng $(0; + \infty)$

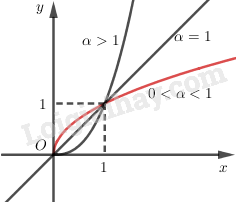
Chú ý: Khi khảo sát hàm số $y = x^{α}$ với $α$ cụ thể, cần xét hàm số trên toàn tập xác định của nó (chứ không phải chỉ xét trên khoảng $(0; + \infty)$ như trên).

Sơ đồ tư duy về hàm số lũy thừa

Các công thức lãi kép

1. Lãi kép theo định kì

- Là thể thức mà hết kì hạn này, tiền lãi được nhập vào vốn của kì tiếp theo.

2. Một số dạng toán về lãi suất

Dạng 1: Bài toán tiết kiệm (Thể thức lãi kép không kỳ hạn)

Một người gửi vào ngân hàng số tiền $A$ đồng, lãi suất $r$ mỗi tháng theo hình thức lãi kép, gửi theo phương thức không kì hạn. Tính số tiền cả vốn lẫn lãi mà người đó nhận được sau $N$ tháng?

Phương pháp xây dựng công thức:

Gọi $T_{N}$ là số tiền cả vốn lẫn lãi sau $N$ tháng. Ta có:

- Sau 1 tháng $(k = 1) : T_{1} = A + A . r = A (1 + r)$ .

- Sau 2 tháng $(k = 2) : T_{2} = A (1 + r) + A (1 + r) . r = A {(1 + r)}^{2}$

…

- Sau $N$ tháng $(k = N) : T_{N} = A {(1 + r)}^{N}$

Vậy số tiền cả vốn lẫn lãi người đó có được sau $N$ tháng là:

$T_{N} = A {(1 + r)}^{N}$

Lãi suất thường được cho ở dạng $a %$ nên khi tính toán ta phải tính $r = a : 100$ rồi mới thay vào công thức.

Dạng 2: Bài toán tiết kiệm (Thể thức lãi kép có kỳ hạn)

Một người gửi vào ngân hàng số tiền $A$ đồng, lãi suất $r$ mỗi tháng theo hình thức lãi kép, gửi theo phương thức có kì hạn $m$ tháng. Tính số tiền cả vốn lẫn lãi mà người đó nhận được sau $N$ kì hạn?

Phương pháp:

Bài toán này tương tự bài toán ở trên, nhưng ta sẽ tính lãi suất theo định kỳ $m$ tháng là: $r^{'} = m . r$ .

Sau đó áp dụng công thức $T_{N} = A {(1 + r^{'})}^{N}$ với $N$ là số kì hạn.

Trong cùng một kì hạn, lãi suất sẽ gống nhau mà không được cộng vào vốn để tính lãi kép.

Ví dụ: Một người gửi tiết kiệm $100$ triệu vào ngân hàng theo mức kì hạn $6$ tháng với lãi suất $0, 65 %$ mỗi tháng. Hỏi sau $10$ năm, người đó nhận được bao nhiêu tiền cả vốn lẫn lãi, biết rằng người đó không rút tiền trong $10$ năm đó.

Giải:

- Số kỳ hạn $N = \frac{10.12}{6} = 20$ kỳ hạn.

- Lãi suất theo định kỳ $6$ tháng là $6.0, 65 % = 3, 9 %$ .

Số tiền cả vốn lẫn lãi người đó có được sau $10$ năm là: $T = 100 {(1 + 3, 9 %)}^{20} = 214, 9$ (triệu)

Dạng 3: Bài toán tích lũy (Hàng tháng (quý, năm,…) gửi một số tiền cố định vào ngân hàng)

Một người gửi vào ngân hàng số tiền $A$ đồng mỗi tháng với lãi suất mỗi tháng là $r$ . Hỏi sau $N$ tháng, người đó có tất cả bao nhiêu tiền trong ngân hàng?

Phương pháp xây dựng công thức:

Gọi $T_{N}$ là số tiền có được sau $N$ tháng.

- Cuối tháng thứ 1: $T_{1} = A (1 + r)$ .

- Đầu tháng thứ 2: $A (1 + r) + A = \frac{A}{r} [{(1 + r)}^{2} - 1]$

- Cuối tháng thứ 2: $T_{2} = \frac{A}{r} [{(1 + r)}^{2} - 1] + \frac{A}{r} [{(1 + r)}^{2} - 1] . r = \frac{A}{r} [{(1 + r)}^{2} - 1] (1 + r)$

…

- Đầu tháng thứ N: $\frac{A}{r} [{(1 + r)}^{N} - 1]$

- Cuối tháng thứ $N : T_{N} = \frac{A}{r} [{(1 + r)}^{N} - 1] (1 + r)$ .

Vậy sau $N$ tháng, số tiền cả vốn lẫn lãi người đó có được là:

$T_{N} = \frac{A}{r} [{(1 + r)}^{N} - 1] (1 + r)$

Dạng 4: Bài toán trả góp.

Một người vay ngân hàng số tiền $T$ đồng, lãi suất định kì là $r$ . Tìm số tiền $A$ mà người đó phải trả cuối mỗi kì để sau $N$ kì hạn là hết nợ.

Phương pháp xây dựng công thức:

- Sau 1 tháng, số tiền gốc và lãi là $T + T . r$ , người đó trả $A$ đồng nên còn: $T + T . r - A = T (1 + r) - A$

- Sau 2 tháng, số tiền còn nợ là: $T (1 + r) - A + [T (1 + r) - A] . r - A = T {(1 + r)}^{2} - \frac{A}{r} [{(1 + r)}^{2} - 1]$

- Sau 3 tháng, số tiền còn nợ là: $T {(1 + r)}^{3} - \frac{A}{r} [{(1 + r)}^{3} - 1]$

- Sau $N$ tháng, số tiền còn nợ là: $T {(1 + r)}^{N} - \frac{A}{r} [{(1 + r)}^{N} - 1]$ .

Vậy sau $N$ tháng, người đó còn nợ số tiền là:

$T {(1 + r)}^{N} - \frac{A}{r} [{(1 + r)}^{N} - 1]$

Khi trả hết nợ thì số tiền còn lại bằng $0$ nên ta có:

$T {(1 + r)}^{N} - \frac{A}{r} [{(1 + r)}^{N} - 1] = 0 \Leftrightarrow A = \frac{T {(1 + r)}^{N} . r}{{(1 + r)}^{N} - 1}$

Xem thêm các chương trình khác:

Bài trước

Bài sau

Giải SGK, SBT, Chuyên đề Toán Học Lớp 12

Giải Toán 12 Bài 2: Hàm số lũy thừa

Xem thêm các chương trình khác: