Chúng tôi giới thiệu Giải bài tập Toán lớp 12 Bài 4: Hàm số mũ. Hàm số lôgarit chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Hàm số mũ - hàm số lôgarit lớp 12.
Giải bài tập Toán lớp 12 Bài 4: Hàm số mũ. Hàm số lôgarit
Phương pháp giải:
Lời giải:
Từ năm đến năm là năm.
Vậy năm Việt Nam sẽ có số người là:
Phương pháp giải:
Lời giải:
Các hàm số mũ là với cơ số là ; với cơ số là ; với cơ số là
Phương pháp giải:
Lời giải:
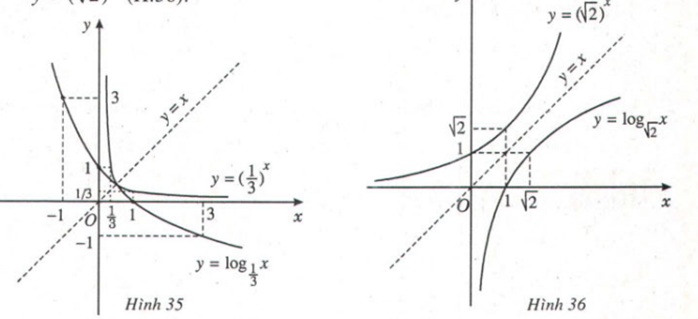
Lời giải:
Đồ thị của các hàm số trên Hình 35 và Hình 36 đối xứng nhau qua đường thẳng
a) ;
Phương pháp giải:
Các bước khảo sát và vẽ đồ thị hàm số:
Bước 1: Tập xác định.
Bước 2: Sự biến thiên.
- Tính , tìm các điểm mà tại đó bằng 0 hoặc không xác định.
- Xét dấu và suy ra các khoảng đơn điệu của đồ thị hàm số.
- Tính các giới hạn đặc biệt: Giới hạn tại vô cực và giới hạn tại các điểm mà hàm số không xác định.
- Tìm các tiệm cận của đồ thị hàm số (nếu có).
- Lập bảng biến thiên.
Bước 3: Đồ thị.
- Tìm giao điểm của đồ thị hàm số với các trục tọa độ (nếu có).
- Vẽ đồ thị hàm số dựa vào các yếu tố ở trên.
Lời giải:
a)
Đồ thị hàm số
*) Tập xác định:
*) Sự biến thiên:
- Hàm số đồng biến trên
- Giới hạn đặc biệt:
Tiệm cận ngang: .
- Bảng biến thiên:
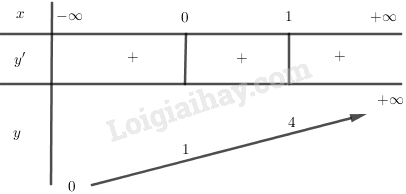
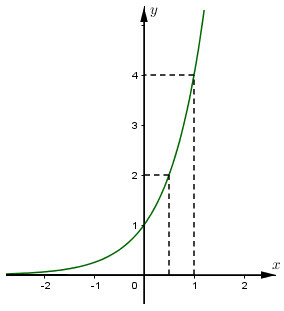
Đồ thị:
Đồ thị nằm hoàn toàn phía trên trục hoành, cắt trục tung tại điểm , đi qua điểm và qua các điểm , , .
b)
Đồ thị hàm số
*) Tập xác định:
*) Sự biến thiên:
- Hàm số nghịch biến trên
- Giới hạn:
Tiệm cận ngang
- Bảng biến thiên:
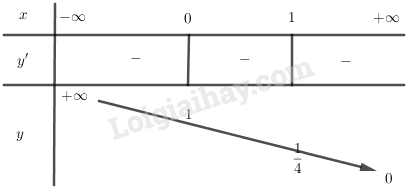
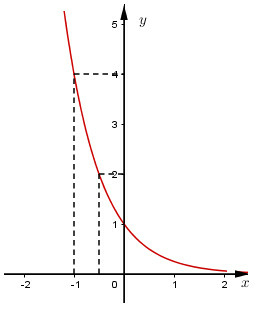
*) Đồ thị:
Đồ thị hàm số nằm hoàn toàn về phía trên trục hoành, cắt trục tung tại điểm đi qua điểm ) và qua các điểm
a) ;
Phương pháp giải:
Sử dụng bảng đạo hàm cơ bản: và quy tắc tính đạo hàm của một tích: .
Lời giải:
a)
b)
c)
a) ;
b) ;
Phương pháp giải:
Hàm số xác định khi và chỉ khi .
Lời giải:
a)
Hàm số xác định khi và chỉ khi:
Vậy hàm số có tập xác định là
b)
Hàm số xác định khi và chỉ khi:
Vậy hàm số có tập xác định là .
c)
Hàm số xác định khi và chỉ khi
Vậy hàm số có tập xác định là .
d)
Hàm số xác định khi và chỉ khi:
Vậy hàm số có tập xác định là .
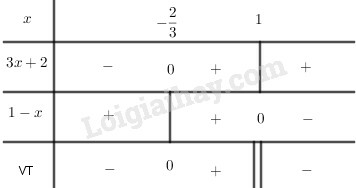
Chú ý:
Các em cũng có thể lập bảng xét dấu các nhị thức bậc nhất như sau:
a) ;
Phương pháp giải:
Các bước khảo sát và vẽ đồ thị hàm số:
Bước 1: Tập xác định.
Bước 2: Sự biến thiên.
- Tính , tìm các điểm mà tại đó bằng 0 hoặc không xác định.
- Xét dấu và suy ra các khoảng đơn điệu của đồ thị hàm số.
- Tính các giới hạn đặc biệt: Giới hạn tại vô cực và giới hạn tại các điểm mà hàm số không xác định.
- Tìm các tiệm cận của đồ thị hàm số (nếu có).
- Lập bảng biến thiên.
Bước 3: Đồ thị.
- Tìm giao điểm của đồ thị hàm số với các trục tọa độ (nếu có).
- Vẽ đồ thị hàm số dựa vào các yếu tố ở trên.
Lời giải:
a)
Đồ thị hàm số .
*) Tập xác định:
*) Sự biến thiên:
- Hàm số đồng biến trên khoảng
- Giới hạn đặc biệt:
Hàm số có tiệm cận đứng là:
- Bảng biến thiên:
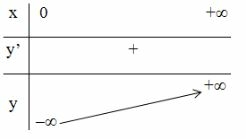
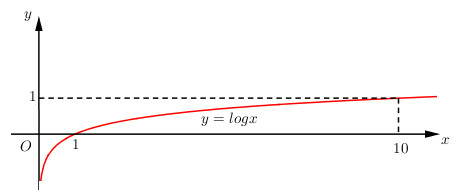
*) Đồ thị:
Đồ thị hàm số nằm hoàn toàn bên phải trục tung) nhận trục tung làm tiệm cận đứng, cắt trục hoành tại điểm và đi qua điểm , .
b)
Đồ thị hàm số .
*) Tập xác định:
*) Sự biến thiên:
- Hàm số nghịch biến trên khoảng
- Giới hạn:
Hàm số có tiệm cận đứng .
- Bảng biến thiên:
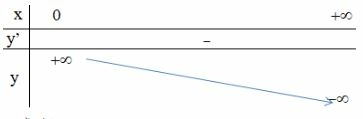
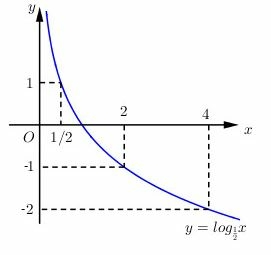
*) Đồ thị:
Đồ thị hàm số nằm hoàn toàn bên phải trục tung (nhận trục tung làm tiệm cận đứng), cắt trục hoành tại điểm và đi qua điểm , điểm phụ , , .
a) ;
Phương pháp giải:
a) Sử dụng bảng đạo hàm cơ bản:
b) Sử dụng công thức đạo hàm của hàm hợp:
c) Sử dụng bảng đạo hàm cơ bản và quy tắc tính đạo hàm của thương: .
Lời giải:
a)
b)
= .
c)
= .
1. Định nghĩa
Hàm số mũ là hàm số có dạng , hàm số lôgarit là hàm số có dạng ( với cơ số a dương khác 1).
2. Tính chất của hàm số mũ .
- Tập xác định: .
- Đạo hàm: .
- Chiều biến thiên
+) Nếu thì hàm số luôn đồng biến
+) Nếu thì hàm số luôn nghịch biến

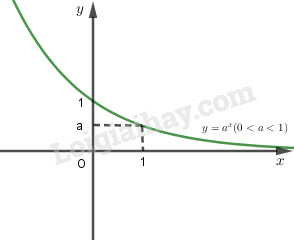
- Tiệm cận: trục là tiệm cận ngang.
- Đồ thị nằm hoàn toàn về phía trên trục hoành , và luôn cắt trục tung tại điểm và đi qua điểm .
3. Tính chất của hàm số lôgarit .
- Tập xác định: .
- Đạo hàm .
- Chiều biến thiên:
+) Nếu thì hàm số luôn đồng biến
+) Nếu thì hàm số luôn nghịch biến
- Tiệm cận: Trục là tiệm cận đứng.
- Đồ thị nằm hoàn toàn phía bên phải trục tung, luôn cắt trục hoành tại điểm và đi qua điểm .

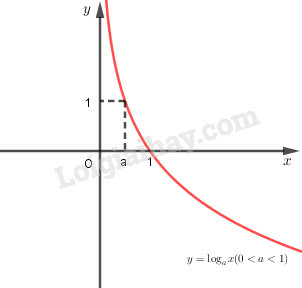
4. Chú ý
- Nếu thì , suy ra và
do đó hàm số mũ và hàm số lôgarit với cơ số lớn hơn 1 đều là những hàm số luôn luôn đồng biến.
Tương tự, nếu thì , và ; hàm số mũ và hàm số lôgarit với cơ số nhỏ hơn 1 đều là những hàm số luôn luôn nghịch biến.
- Công thức đạo hàm của hàm số lôgarit có thể mở rộng thành
và
Sơ đồ tư duy về Hàm số mũ - Hàm số Lôgarit
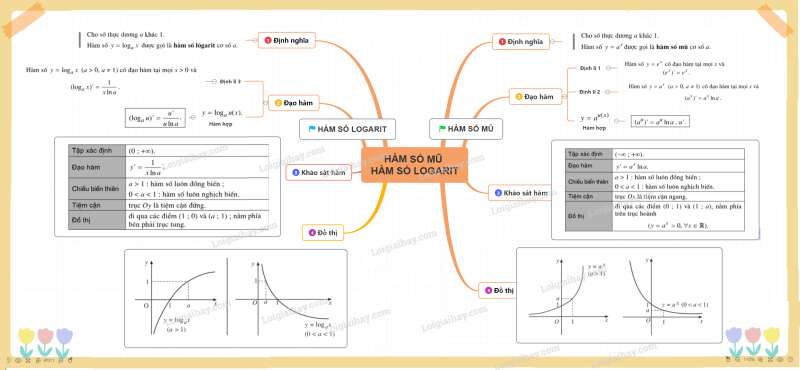
1. Hàm số mũ
Dạng 1: Tìm hàm số có đồ thị cho trước và ngược lại.
Phương pháp:
- Bước 1: Quan sát dáng đồ thị, tính đơn điệu,…của các đồ thị bài cho.
- Bước 2: Đối chiếu với hàm số bài cho và chọn kết luận.
Dạng 2: Tìm mối quan hệ giữa các cơ số khi biết đồ thị.
Phương pháp:
- Bước 1: Quan sát các đồ thị, nhận xét về tính đơn điệu để nhận xét các cơ số.
+ Hàm số đồng biến thì cơ số lớn hơn .
+ Hàm số nghịch biến thì cơ số lớn hơn và nhỏ hơn .
- Bước 2: So sánh các cơ số dựa vào phần đồ thị của hàm số.
- Bước 3: Kết hợp các điều kiện ở trên ta được mối quan hệ cần tìm.
Lưu ý: Đối với một số bài toán phức tạp hơn thì ta cần chú ý thêm đến một số yếu tố khác như điểm đi qua, tính đối xứng,…
Dạng 3: Tính đạo hàm các hàm số.
Phương pháp:
- Bước 1: Áp dụng các công thức tính đạo hàm của tổng, hiệu, tích, thương để tính đạo hàm hàm số đã cho.
- Bước 2: Tính đạo hàm các hàm số thành phần dựa vào công thức tính đạo hàm các hàm số cơ bản: hàm đa thức, phân thức, hàm mũ, logarit, lũy thừa,…
- Bước 3: Tính toán và kết luận.
Dạng 4: Tính giới hạn các hàm số.
Phương pháp:
Áp dụng các công thức tính giới hạn đặc biệt để tính toán:
; ; ; .
Dạng 5: Tìm GTLN, GTNN của hàm số mũ trên một đoạn.
Phương pháp:
- Bước 1: Tính , tìm các nghiệm của phương trình .
- Bước 2: Tính .
- Bước 3: So sánh các giá trị vừa tính ở trên và kết luận GTLN, GTNN của hàm số.
+ GTNN là số nhỏ nhất trong các giá trị tính được.
+ GTLN là số lớn nhất trong các giá trị tính được.
2. Hàm số logarit
Dạng 1: Tìm tập xác định của hàm số.
Phương pháp:
- Bước 1: Tìm điều kiện để các logarit xác định.
Hàm số xác định
- Bước 2: Tìm điều kiện để các biểu thức dưới dấu căn bậc hai, biểu thức dưới mẫu trong các phân thức,…(nếu có).
+ Căn bậc hai xác định nếu .
+ Phân thức xác định nếu .
- Bước 3: Giải các bất phương trình ở trên và kết hợp nghiệm ta được tập xác định của hàm số.
Dạng 2: Tìm hàm số có đồ thị cho trước và ngược lại.
Phương pháp:
- Bước 1: Quan sát dáng đồ thị, tính đơn điệu,…của các đồ thị bài cho.
- Bước 2: Đối chiếu với hàm số bài cho và chọn kết luận.
Dạng 3: Tìm mối quan hệ giữa các cơ số khi biết đồ thị.
Phương pháp:
- Bước 1: Quan sát các đồ thị, nhận xét về tính đơn điệu để nhận xét các cơ số.
+ Hàm số đồng biến thì cơ số lớn hơn .
+ Hàm số nghịch biến thì cơ số lớn hơn và nhỏ hơn .
- Bước 2: So sánh các cơ số dựa vào phần đồ thị của hàm số.
- Bước 3: Kết hợp các điều kiện ở trên ta được mối quan hệ cần tìm.
Lưu ý: Đối với một số bài toán phức tạp hơn thì ta cần chú ý thêm đến một số yếu tố khác như điểm đi qua, tính đối xứng,…
Dạng 4: Tính đạo hàm các hàm số.
Phương pháp:
- Bước 1: Áp dụng các công thức tính đạo hàm của tổng, hiệu, tích, thương để tính đạo hàm hàm số đã cho.
- Bước 2: Tính đạo hàm các hàm số thành phần dựa vào công thức tính đạo hàm các hàm số cơ bản: hàm đa thức, phân thức, hàm mũ, logarit, lũy thừa,…
- Bước 3: Tính toán và kết luận.
Dạng 5: Tính giới hạn các hàm số.
Phương pháp:
Áp dụng các công thức tính giới hạn đặc biệt để tính toán:
;
Dạng 6: Tìm GTLN, GTNN của hàm số mũ và hàm số logarit trên một đoạn.
Phương pháp:
- Bước 1: Tính , tìm các nghiệm của phương trình .
- Bước 2: Tính .
- Bước 3: So sánh các giá trị vừa tính ở trên và kết luận GTLN, GTNN của hàm số.
+ GTNN là số nhỏ nhất trong các giá trị tính được.
+ GTLN là số lớn nhất trong các giá trị tính được.

