Chúng tôi giới thiệu Giải bài tập Toán lớp 12 Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Khảo sát sự biến thiên và vẽ đồ thị của hàm số lớp 12.
Giải bài tập Toán lớp 12 Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Phương pháp giải:
B1: Tìm TXĐ
B2: Bảng biến thiên
- Xét chiều biến thiên
+Tính .
+ Tìm các điểm mà tại đó hàm số không xác định và nghiệm của .
+ Xét dấu đạo hàm suy ra chiều biến thiên
- Tìm cực trị
- Tính các giới hạn,tiệm cận (nếu có).
- Lập bảng biến thiên
B3: Vẽ đồ thị
Lời giải:
* Hàm số
Trường hợp a > 0
1. TXĐ:
2. Sự biến thiên.
. Vậy hàm số đồng biến trên toàn bộ R.
Bảng biến thiên
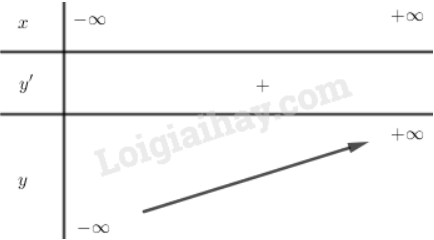
3. Vẽ đồ thị
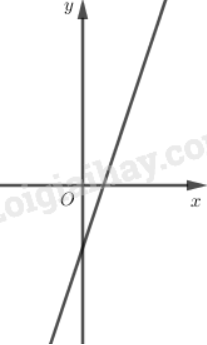
Trường hợp
1. TXĐ:
2. Sự biến thiên.
Vậy hàm số đồng biến trên toàn bộ
Bảng biến thiên
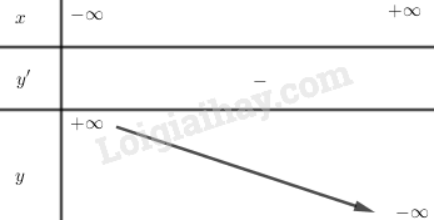
Vẽ đồ thị
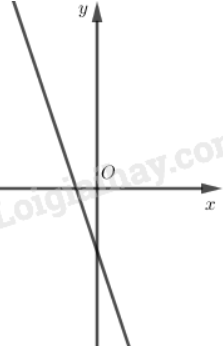
* Hàm số
Trường hợp
1. TXĐ:
2. Sự biến thiên.
Bảng biến thiên
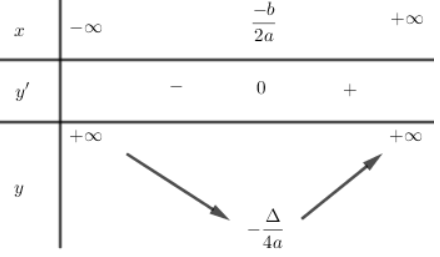
Hàm số nghịch biến trên khoảng (-∞, ).
Hàm số đồng biến trên khoảng (, +∞).
Hàm số đạt cực tiểu bằng tại
Vẽ đồ thị
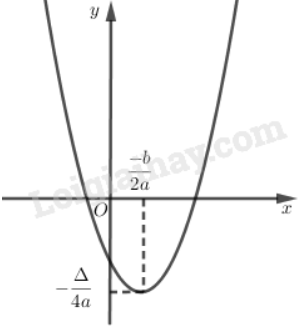
Trường hợp
1. TXĐ:
2. Sự biến thiên.
Cho
Bảng biến thiên
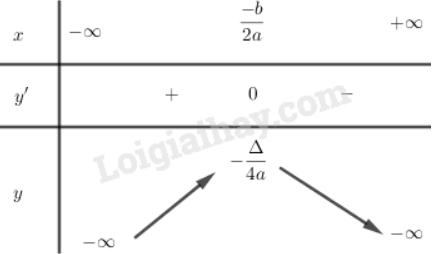
Hàm số đồng biến trên khoảng (-∞, ).
Hàm số nghịch biến trên khoảng .
Hàm số đạt cực đại bằng tại
Vẽ đồ thị
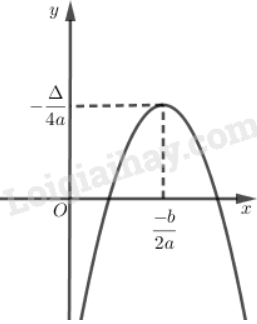
Nêu nhận xét về đồ thị của hàm số này với đồ thị của hàm số khảo sát trong Ví dụ 1.
Phương pháp giải:
B1: Tìm TXĐ
B2: Bảng biến thiên
- Xét chiều biến thiên
+Tính .
+ Tìm các điểm mà tại đó hàm số không xác định và nghiệm của .
+ Xét dấu đạo hàm suy ra chiều biến thiên
- Tìm cực trị
- Tính các giới hạn,tiệm cận (nếu có).
- Lập bảng biến thiên
B3: Vẽ đồ thị
Lời giải:
TXĐ:
Sự biến thiên:
Cho hoặc
Bảng biến thiên
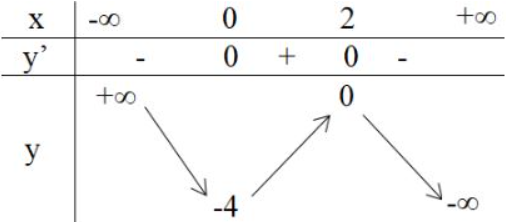
Hàm số đồng biến trên khoảng
Hàm số nghịch biến trên các khoảng
Hàm số đạt cực đại bằng 0 tại
Hàm số đạt cực tiểu bằng -4 tại
Vẽ đồ thị hàm số
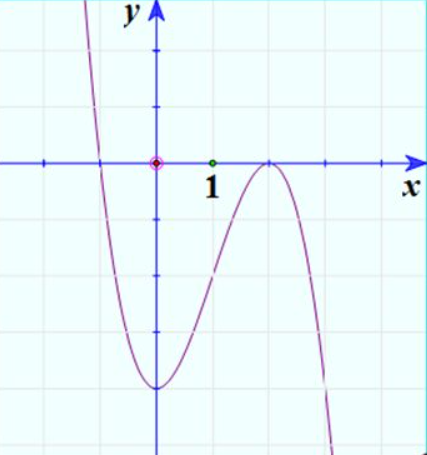
Nhận xét: hai đồ thị đối xứng nhau qua
Phương pháp giải:
B1: Tìm TXĐ
B2: Bảng biến thiên
- Xét chiều biến thiên
+Tính .
+ Tìm các điểm mà tại đó hàm số không xác định và nghiệm của .
+ Xét dấu đạo hàm suy ra chiều biến thiên
- Tìm cực trị
- Tính các giới hạn,tiệm cận (nếu có).
- Lập bảng biến thiên
B3: Vẽ đồ thị
Lời giải:
1.TXĐ:
2. Sự biến thiên:
với mọi . Vậy hàm số đồng biến trên toàn bộ
Cho
Bảng biến thiên
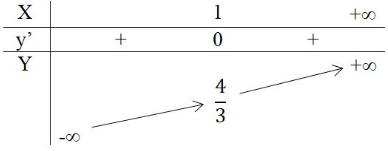
Vẽ đồ thị hàm số
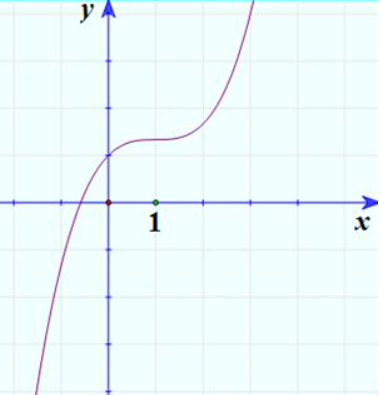
Bằng đồ thị, biện luận theo số nghiệm của phương trình
Lời giải:
* Khảo sát sự biến thiên và vẽ đồ thị của hàm số
1.TXĐ: .
2. Sự biến thiên:
Cho hoặc
Bảng biến thiên
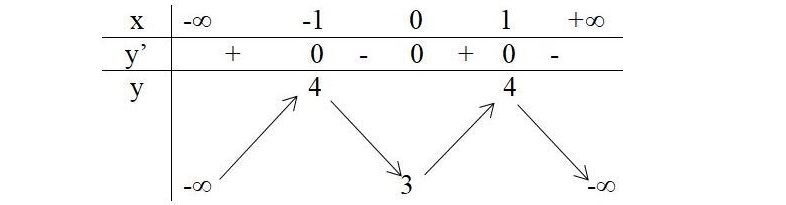
Hàm số đồng biến trên:
Hàm số nghịch biến trên:
Hàm số đạt cực đại bằng 4 tại và
Hàm số đạt cực tiểu bằng 3 tại
Đồ thị
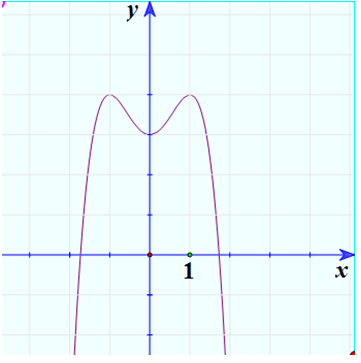
* Giải biện luận phương trình
Số giao điểm của hai đồ thị và là số nghiệm của phương trình trên.
Với Hai đồ thị không giao nhau nên phương trình vô nghiệm.
Với hoặc Hai đồ thị giao nhau tại 2 điểm phân biệt nên phương trình có hai nghiệm phân biệt.
Với . Hai đồ thị giao nhau tại 3 điểm phân biệt nên phương trình có ba nghiệm phân biệt.
Với Hai đồ thị giao nhau tại 4 điểm phân biệt nên phương trình có bốn nghiệm phân biệt.
Lời giải:
Ví dụ hàm số
Có đạo hàm
Cho thì
Phương pháp giải:
Cho hai đồ thị hàm số và
Hoành độ giao điểm là nghiệm của pt
Thay tìm được vào hoặc để được tung độ.
Lời giải:
Xét phương trình hoành độ giao điểm:
hoặc
Với thì .
Với thì
Vậy tọa độ giao điểm là và .
a) ;
b) ;
c) ;
d)
Phương pháp giải:
Các bước khảo sát sự biến thiên và vẽ đồ thị hàm số:
Bước 1: Tìm TXĐ của hàm số.
Bước 2: Khảo sát sự biến thiên:
*) Xét chiều biến thiên của hàm số:
+) Tính đạo hàm.
+) Tìm các điểm mà tại đó đạo hàm có hoặc đạo hàm không xác định.
+) Xét dấu đạo hàm y’ và suy ra chiều biến thiên của hàm số.
*) Tìm cực trị:
*) Tìm các giới hạn vô cực, các giới hạn có kết quả là vô cực và tiệm cận của đồ thị hàm số nếu có. ( )
*) Lập bảng biến thiên: Thể hiện đầy đủ và chính xác các giá trị trên bảng biến thiên.
Bước 3: Đồ thị:
+) Giao điểm của đồ thị với trục tung:
+) Giao điểm của đồ thị với trục hoành:
+) Các điểm cực đại, cực tiểu nếu có.
Lời giải:
a)
1) TXĐ:
2) Sự biến thiên:
+) Chiều biến thiên:
Ta có:
Trên khoảng nên hàm số số đồng biến, trên khoảng và có nên hàm số nghịch biến.
+) Cực trị: Hàm số đạt cực đại tại Hàm số đạt cực tiểu tại
+) Giới hạn vô cực:
+) Bảng biến thiên:
+) Đồ thị:
Ta có:
Vậy đồ thị hàm số giao với trục hoành tại 2 điểm và
Ta có: ; . Với ta có . Vậy đồ thị hàm số nhận điểm làm tâm đối xứng.
Nhận thấy, nhánh bên trái vẫn còn thiếu một điểm để vẽ đồ thị, dựa vào tính đối xứng ta chọn điểm của hoành độ suy ra .
b)
Xét hàm số
Tập xác định:
Sự biến thiên:
Đạo hàm: .
Hàm số đồng biến trên các khoảng và và nghịch biến trên
Cực trị:
Hàm số đạt cực đại tại , giá trị cực đại cđ = .
Hàm số đạt cực tiểu tại , giá trị cực tiểu
Giới hạn:
Bảng biến thiên:
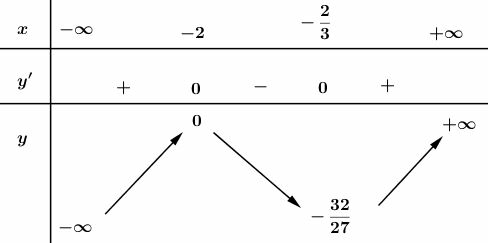
Đồ thị hàm số cắt trục tại điểm , cắt trục tại điểm có hoành độ là nghiệm của phương trình: hoặc nên tọa độ các giao điểm là và .
Đồ thị hàm số:
Tâm đối xứng của đồ thị hàm số:
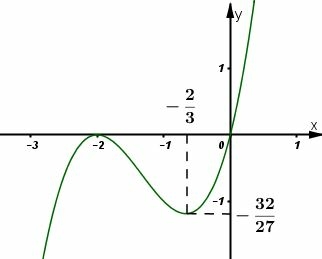
c)
Xét hàm số
Tập xác định:
Sự biến thiên:
Đạo hàm:
Vậy hàm số luôn đồng biến trên và không có cực trị.
Giới hạn:
Bảng biến thiên :
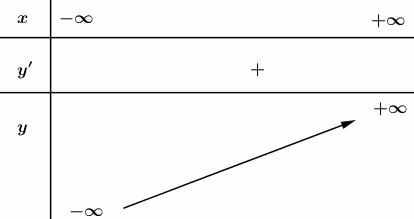
Đồ thị:
Đồ thị hàm số cắt trục tại điểm , cắt trục tại điểm .
Tâm đối xứng:
Suy ra tọa độ tâm đối xứng là:
Đồ thị hàm số đi qua các điểm và
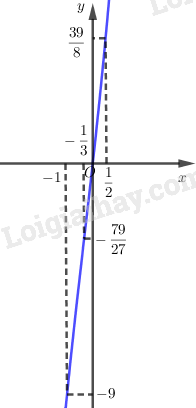
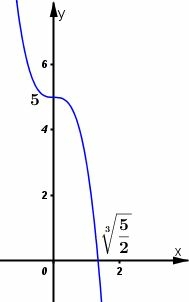
d)
Xét hàm số
Tập xác định:
Sự biến thiên:
Đạo hàm: .
Vậy hàm số luôn nghịch biến trên .
Hàm số không có cực trị.
Giới hạn:
Bảng biến thiên:
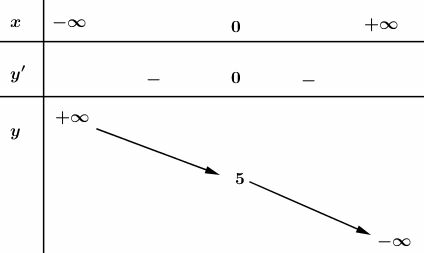
Đồ thị:
Tính đối xứng: .
Vậy đồ thị hàm số nhận điểm uốn làm tâm đối xứng.
Đồ thị hàm số cắt trục tại điểm , đồ thị cắt trục tại điểm
a) ;
b) ;
c) ;
d) .
Phương pháp giải:
Các bước khảo sát sự biến thiên và vẽ đồ thị hàm số:
Bước 1: Tìm TXĐ của hàm số.
Bước 2: Khảo sát sự biến thiên:
*) Xét chiều biến thiên của hàm số:
+) Tính đạo hàm.
+) Tìm các điểm mà tại đó đạo hàm có hoặc đạo hàm không xác định.
+) Xét dấu đạo hàm y’ và suy ra chiều biến thiên của hàm số.
*) Tìm cực trị:
*) Tìm các giới hạn vô cực, các giới hạn có kết quả là vô cực và tiệm cận của đồ thị hàm số nếu có:
*) Lập bảng biến thiên: Thể hiện đầy đủ và chính xác các giá trị trên bảng biến thiên.
Bước 3: Đồ thị:
+) Giao điểm của đồ thị với trục tung:
+) Giao điểm của đồ thị với trục hoành:
+) Các điểm cực đại, cực tiểu nếu có.
Lời giải:
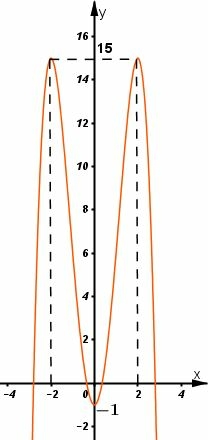
a)
Tập xác định: ;
Sự biến thiên:
Ta có:
- Hàm số đồng biến trên khoảng và ; nghịch biến trên khoảng và .
- Cực trị:
Hàm số đạt cực đạt tại hai điểm và ; .
Hàm số đạt cực tiểu tại ;
- Giới hạn:
Bảng biến thiên:
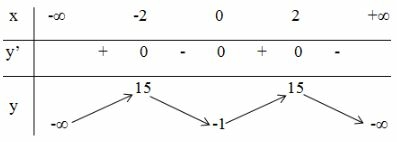
Đồ thị giao tại điểm
Hàm số đã cho là hàm số chẵn nhận trục làm trục đối xứng.
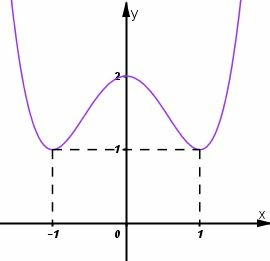
Đồ thị
b)
Tập xác định: ;
Sự biến thiên:
Ta có: ;
- Hàm số đồng biến trên khoảng và ; nghịch biến trên khoảng và .
- Cực trị:
Hàm số đạt cực đại tại ; .
Hàm số đạt cực tiểu tại hai điểm và ; .
-Giới hạn:
Bảng biến thiên:
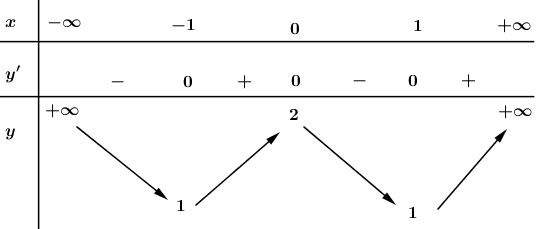
Hàm số đã cho là hàm số chẵn nhận trục làm trục đối xứng.
Đồ thị giao tại điểm
Đồ thị
c)
Tập xác định: ;
Sự biến thiên:
Ta có: ;
- Hàm số nghịch biến trên khoảng ; đồng biến trên khoảng .
-Cực trị:
Hàm số đạt cực tiểu tại ;
-Giới hạn:
Bảng biến thiên :
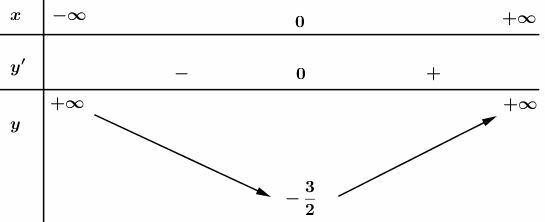
Hàm số đã cho là hàm số chẵn, nhận trục làm trục đối xứng.
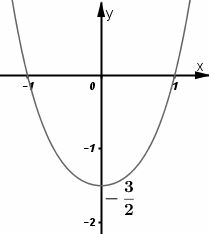
Đồ thị giao tại hai điểm và ; giao tại .
Đồ thị như hình bên.
d)
Tập xác định: ;
Sự biến thiên:
Ta có: ;
- Hàm số đồng biến trên khoảng: ; nghịch biến trên khoảng: .
- Cực trị: Hàm số đạt cực đạt tại ; .
- Giới hạn:
Bảng biến thiên:
Hàm số đã cho là hàm chẵn, nhận trục làm trục đối xứng.
Đồ thị giao tại hai điểm và ; giao tại điểm .
Đồ thị như hình bên.
a) ,
b) ,
c)
Phương pháp giải:
Các bước khảo sát sự biến thiên và vẽ đồ thị hàm số:
Bước 1: Tìm TXĐ của hàm số.
Bước 2: Khảo sát sự biến thiên:
*) Xét chiều biến thiên của hàm số:
+) Tính đạo hàm.
+) Tìm các điểm mà tại đó đạo hàm có hoặc đạo hàm không xác định.
+) Xét dấu đạo hàm y’ và suy ra chiều biến thiên của hàm số.
*) Tìm cực trị:
*) Tìm các giới hạn vô cực, các giới hạn có kết quả là vô cực và tiệm cận của đồ thị hàm số (nếu có):
*) Lập bảng biến thiên: Thể hiện đầy đủ và chính xác các giá trị trên bảng biến thiên.
Bước 3: Đồ thị:
+) Giao điểm của đồ thị với trục tung:
+) Giao điểm của đồ thị với trục hoành:
+) Các điểm cực đại, cực tiểu nếu có.
Lời giải:
a)
Tập xác định : ;
* Sự biến thiên:
Ta có: ;
- Hàm số nghịch biến trên khoảng: và .
- Cực trị:
Hàm số không có cực trị.
- Tiệm cận:
, ;
Do đó, tiệm cận đứng là: ; tiệm cận ngang là: .
Bảng biến thiên:
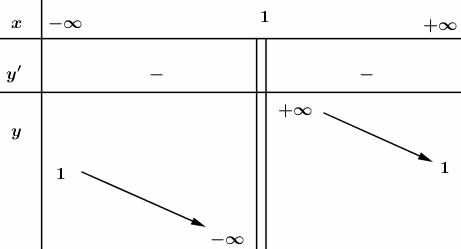
* Đồ thị:
Đồ thị nhận điểm làm tâm đối xứng.
Đồ thị giao trục tung tại:, trục hoành tại
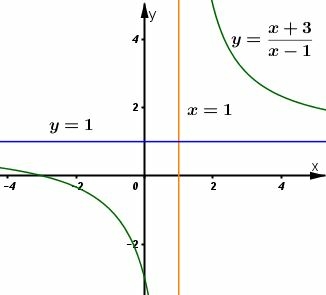
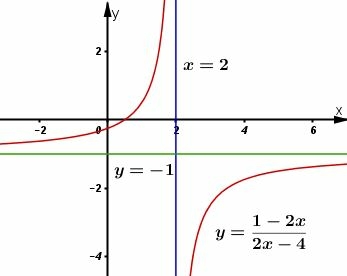
b)
Tập xác định : ;
* Sự biến thiên:
Ta có:
- Hàm số đồng biến trên khoảng: và
- Cực trị:
Hàm số không có cực trị.
- Tiệm cận:
, ,
Do đó, tiệm cận đứng là: ; tiệm cận ngang là:.
Bảng biến thiên :
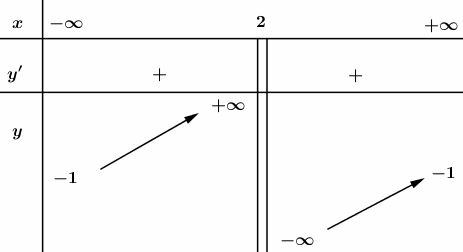
* Đồ thị:
Đồ thị nhận điểm lầm tâm đối xứng.
Đồ thị giao trục tung tại: , trục hoành tại:
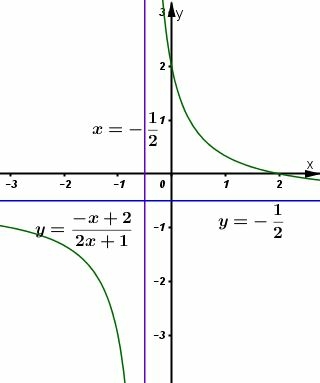
c)
Tập xác định : ;
Sự biến thiên:
Ta có:
- Hàm số nghịch biến trên khoảng: và
- Cực trị:
Hàm số không có cực trị.
- Tiệm cận:
, ,
Do đó, tiệm cận đứng là: ; tiệm cận ngang là: .
Bảng biến thiên :
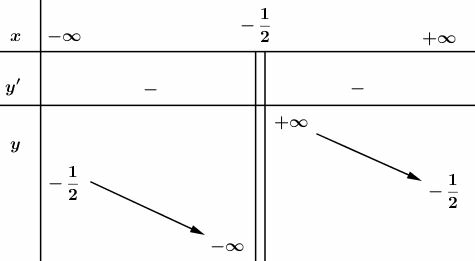
* Đồ thị
Đồ thị nhận điểm làm tâm đối xứng.
Đồ thị giao tại: , tại:
a) ;
b) ;
c) .
Phương pháp giải:
+) Khảo sát sự biến thiên của các hàm số lập bảng biến thiên, vẽ đồ thị hàm số.
+) Số nghiệm của phương trình là số giao điểm của đồ thị hàm số với đường thẳng
+) Khi đó dựa vào đồ thị hàm số để xác định số giao điểm và kết luận.
Lời giải:
a)
Xét hàm số:
+) Tập xác định:
+) Sự biến thiên:
Ta có:
Hàm số đồng biến trên khoảng và ; hàm số nghịch biến trên khoảng
Hàm số đạt cực đại tại
Hàm số đạt cực tiểu tại
+) Giới hạn:
Bảng biến thiên:
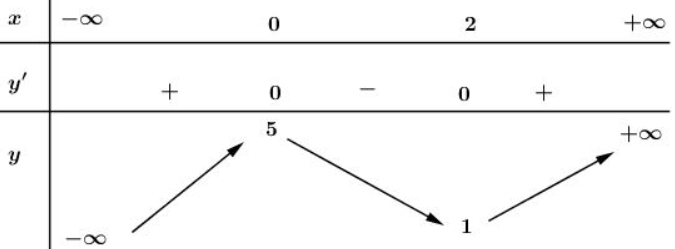
+) Đồ thị hàm số:
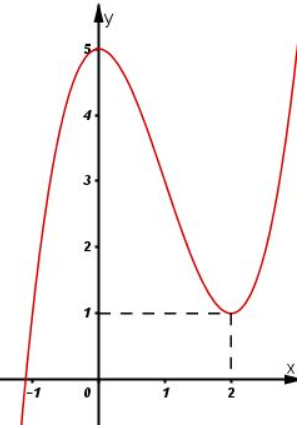
Đồ thị hàm số cắt trục tại điểm
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số và trục hoành.
Từ đồ thị hàm số ta thấy đồ thị hàm số giao với trục hoành tại 1 điểm duy nhất.
Vậy phương trình đã cho có nghiệm duy nhất.
b)
Ta có: (*)
Xét hàm số:
Tập xác định:
Ta có:
Hàm số đồng biến trên khoảng và nghịch biến trên khoảng
Hàm số đạt cực đại tại
Hàm số đạt cực tiểu tại
Giới hạn:
Bảng biến thiên:
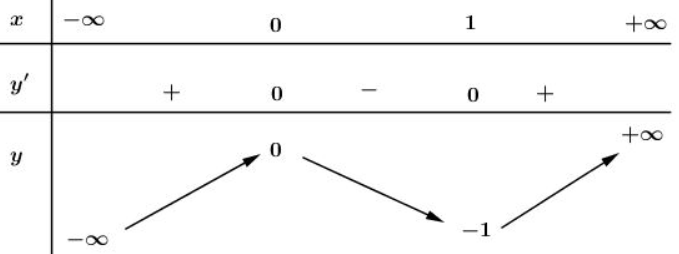
Đồ thị:
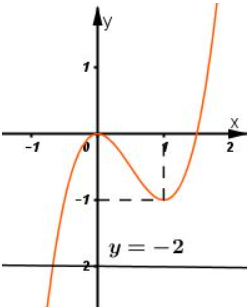
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số và đường thẳng
Dựa vào đồ thị hàm số ta thấy đường thẳng cắt đồ thị hàm số tại 1 điểm duy nhất.
Vậy phương trình đã cho có nghiệm duy nhất.
Cách khác:
Xét hàm số
- TXĐ:
- Sự biến thiên:
+ Chiều biến thiên:
+ Giới hạn:
+ Bảng biến thiên:
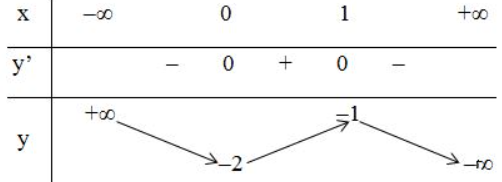
- Đồ thị:
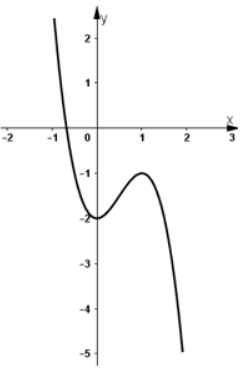
Đồ thị hàm số cắt trục hoành tại 1 điểm duy nhất
⇒ phương trình có nghiệm duy nhất.
Vậy phương trình chỉ có một nghiệm.
c)
Xét hàm số:
Tập xác định:
Sự biến thiên:
Hàm số đồng biến trên khoảng và hàm số nghịch biến trên khoảng và
Hàm số đạt cực đại tại hai điểm và
Hàm số đạt cực tiểu tại
Giới hạn:
Bảng biến thiên:
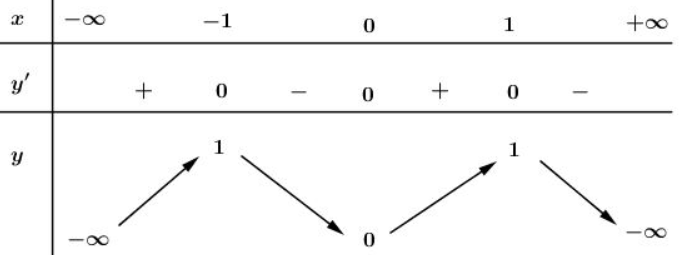
Đồ thị:
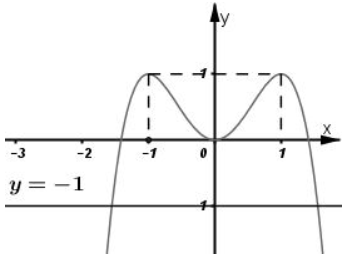
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số và đường thẳng
Dựa vào đồ thị hàm số ta thấy đường thẳng cắt đồ thị hàm số tại hai điểm phân biệt.
Vậy phương trình đã cho có 2 nghiệm phân biệt.
.
b) Dựa vào đồ thị , biện luận về số nghiệm của phương trình sau theo tham số .
.
Phương pháp giải:
- Khảo sát và vẽ đồ thị hàm số bậc 3.
- Dựa vào đồ thị hàm số câu a để biện luận số nghiệm của phương trình.
+) Số nghiệm của phương trình là số giao điểm của đồ thị hàm số với đường thẳng
+) Khi đó dựa vào đồ thị hàm số để xác định số giao điểm và kết luận.
Lời giải:
a)
Xét hàm số .
Tập xác định : .
* Sự biến thiên:
Ta có: ;
.
- Hàm số đồng biến trên khoảng , nghịch biến trên khoảng và .
- Cực trị:
Hàm số đạt cực đại tại ;
Hàm số đạt cực tiểu tại ;
- Giới hạn:
Bảng biến thiên:
* Đồ thị:
Đồ thị giao tại điểm và nhận làm tâm đối xứng.
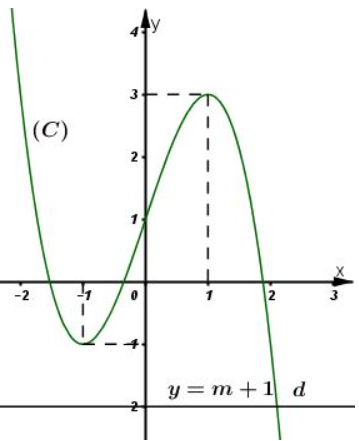
b)
(1). Số nghiệm của (1) chính là số giao điểm của đồ thị hàm số (C) với đường thẳng (d) : .
Từ đồ thị ta thấy :
+) : (d) cắt (C) tại 1 điểm, (1) có 1 nghiệm.
+) : (d) cắt (C) tại 1 điểm và tiếp xúc với (C) tại 1 điểm, (1) có 2 nghiệm.
+) : (d) cắt (C) tại 3 điểm, (1) có 3 nghiệm.
+) : (d) cắt (C) tại 1 điểm và tiếp xúc với (C) tại 1 điểm, (1) có 2 nghiệm.
+) : (d) cắt (C) tại 1 điểm, (1) có 1 nghiệm.
Kết luận:
+ Với m < -2 hoặc m > 2 thì phương trình có 1 nghiệm.
+ Với m = -2 hoặc m = 2 thì phương trình có 2 nghiệm.
+ Với -2 < m < 2 thì phương trình có 3 nghiệm.
a) Chứng minh rằng với mọi giá trị của tham số , hàm số luôn đồng biến trên mỗi khoảng xác định của nó.
Phương pháp giải:
a) Tính đạo hàm của hàm số: , chỉ ra
b) Xác định đường tiệm cận của đồ thị hàm số theo m. Sau đó thế tọa độ của điểm A vào phương trình đường tiệm cận để tìm m.
c) Thay giá trị của m đã cho vào công thức hàm số sau đó khảo sát và vẽ đồ thị hàm số.
Lời giải:
a)
.
Tập xác định: ;
Ta có:
Do đó hàm số luôn đồng biến trên mỗi khoảng xác định của nó.
b)
Tiệm cận đứng : .
Vì .
c)
Với thì hàm số đã cho có phương trình là: .
Tập xác đinh:
* Sự biến thiên:
Ta có:
- Hàm số đồng biến trên khoảng: và
- Cực trị:
Hàm số không có cực trị.
- Tiệm cận:
Tiệm cận đứng là , tiệm cận ngang là:
- Bảng biến thiên
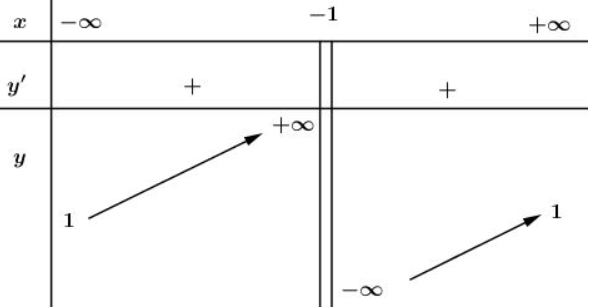
* Đồ thị
Đồ thị hàm số giao tại điểm , giao tại điểm .
Đồ thị hàm số nhận điểm làm tâm đối xứng.
Phương pháp giải:
a) Thay tọa độ điểm đề bài đã cho vào công thức hàm số để tìm m.
b) Thay giá trị m đã cho vào công thức hàm số, sau đó khảo sát và vẽ đồ thị hàm số theo các bước.
c) Xác định tọa độ điểm đề bài cho tung độ bằng cách thay tung độ đề bài đã cho vào công thức hàm số để tìm hoành độ các điểm đó.
+) Viết phương trình tiếp tuyến của đồ thị hàm số tại bằng công thức: .
Lời giải:
a)
Điểm thuộc đồ thị của hàm số .
b)
Với .
Tập xác định:.
* Sự biến thiên:
Ta có: .
- Hàm số đồng biến trên khoảng , nghịch biến trên khoảng
- Cực trị:
Hàm số đạt cực tiểu tại ;
- Giới hạn: ,
- Bảng biến thiên:
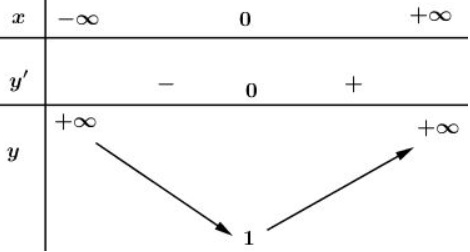
* Đồ thị
Đồ thị hàm số giao trục tại điểm .
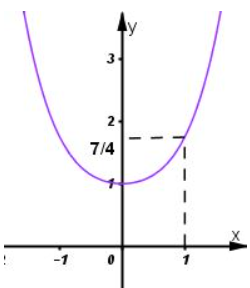
c)
Gọi điểm M thuộc đồ thị hàm số và có tung độ bằng là: .
Khi đó:
Phương trình tiếp tuyến của tại là:
Phương trình tiếp tuyến của tại là:
Phương pháp giải:
a) Tính và rồi suy ra và
Hàm số đạt cực đại tại điểm
b) Đồ thị hàm số cắt trục hoành tại điểm có M hoành độ . Thay tọa độ điểm M vào công thức hàm số để tìm m.
Lời giải:
a)
Ta có:
Hàm số đạt cực đại tại điểm
Vậy thì hàm số đã cho đạt cực đại tại .
b)
Đồ thị hàm số cắt trục hoành tại điểm có M hoành độ .
a) Xác định để đồ thị đi qua điểm .
Phương pháp giải:
a) .Thay vào biểu thức trên để tìm m
b) Thay giá trị m đã tìm được ở câu a vào đồ thị hàm số sau đó khảo sát và vẽ đồ thị hàm số.
c) Đồ thị hàm số cắt trục tung tại điểm có M tung độ .
+) Viết phương trình tiếp tuyến của đồ thị hàm số tại bằng công thức: .
Lời giải:
a)
Theo đề bài ta có
b)
Với ta được hàm số (G0).
Tập xác định:
* Sự biến thiên:
Ta có:
- Hàm số nghịch biến trên khoảng: và .
- Cực trị:
Hàm số không có cực trị.
- Tiệm cận:
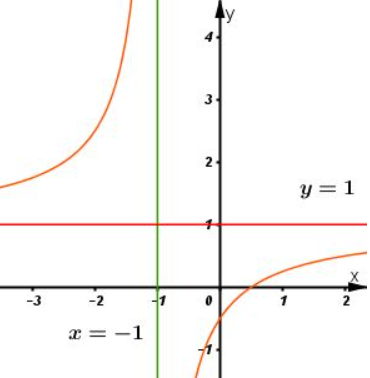
Tiệm cận đứng là: , tiệm cận ngang là:
- Bảng biến thiên:

* Đồ thị:
Đồ thị hàm số giao trục tại , trục tại
Đồ thị hàm số nhận làm tâm đối xứng.
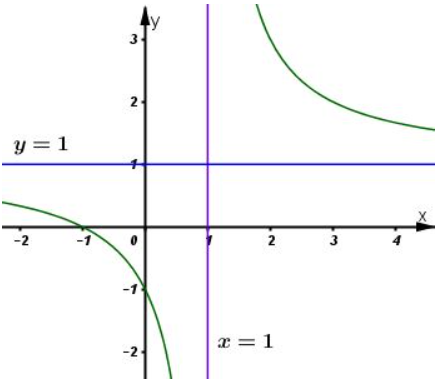
c)
(G0) cắt trục tung tại .
.
Phương trình tiếp tuyến của (G0) tại là:
Dành cho chương trình cơ bản
1. Các bước khảo sát và vẽ đồ thị hàm số y = f(x)
i) Tìm tập xác định của hàm số.
ii) Sự biến thiên
+ Xét sự biến thiên của hàm số
- Tìm đạo hàm bậc nhất ;
- Tìm các điểm tại đó bằng 0 hoặc không xác định ;
- Xét dấu và suy ra chiều biến thiên của hàm số.
+ Tìm cực trị.
+ Tìm các giới hạn tại vô cực, các giới hạn vô cực và tìm các tiệm cận (nếu có).
+ Lập bảng biến thiên tổng kết các bước trên để hình dung ra dáng điệu của đồ thị
iii) Vẽ đồ thị (thể hiện các cực trị, tiệm cận, giao của đồ thị với các trục, . . .)
2. Bảng tóm tắt một số dạng đồ thị thường gặp
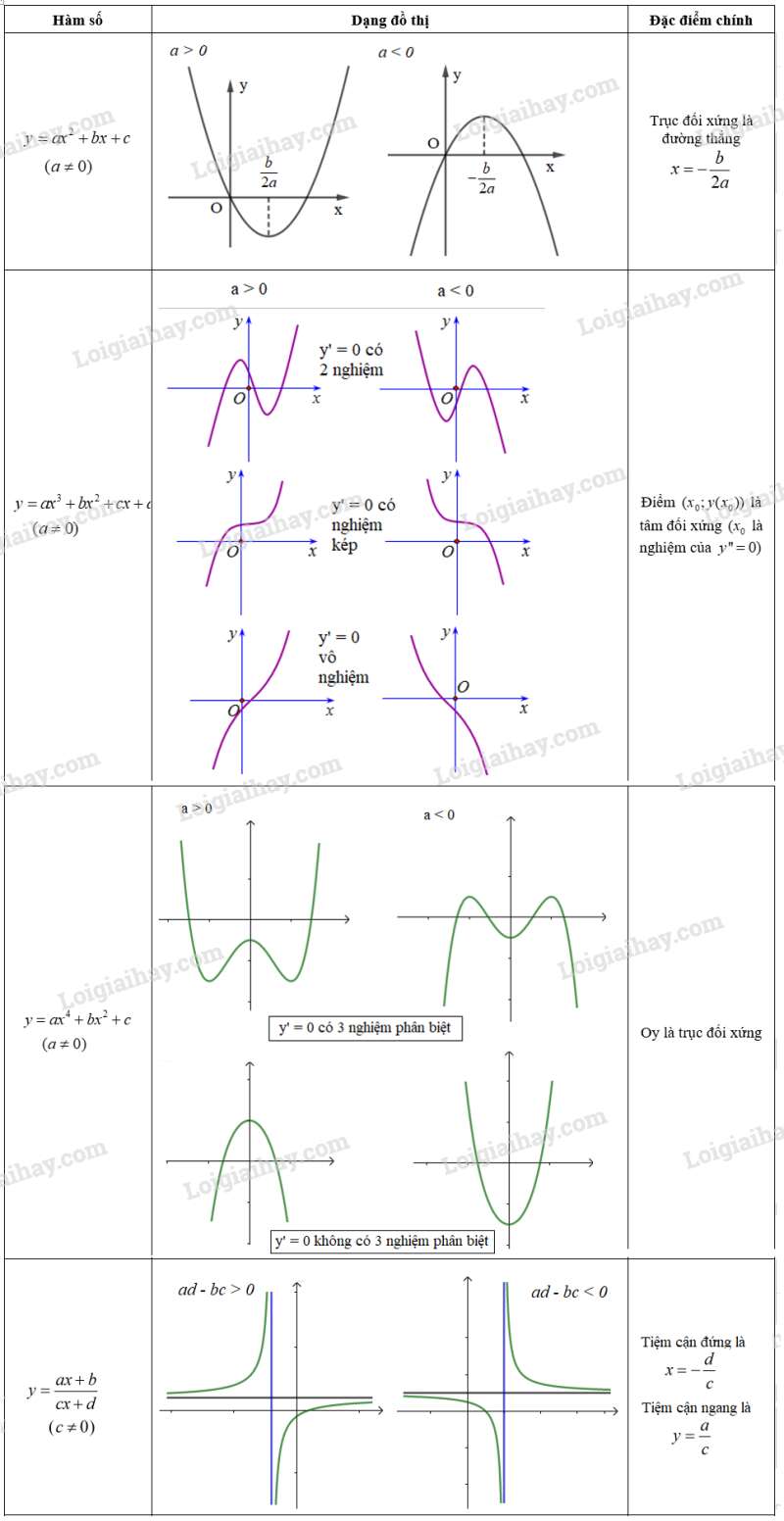
3. Tương giao của các đồ thị
Cho hai đồ thị và
Phương trình xác định hoành độ giao điểm của và là: (1)
- Nếu (1) vô nghiệm thì và không có điểm chung (không cắt nhau và không tiếp xúc với nhau).
- Nếu (1) có nghiệm phân biệt thì và giao nhau tại điểm phân biệt. Nghiệm của (1) chính là hoành độ các giao điểm.
Chú ý
a) tiếp xúc với hệ có nghiệm. Nghiệm của hệ là hoành độ tiếp điểm của hai đồ thị đó.
b) Đường thẳng (d): y: mx+n tiếp xúc với parabol ()
hệ có nghiệm
phương trình có nghiệm kép.
Dành cho chương trình nâng cao
1. Chứng minh là tâm đối xứng của đồ thị (C) của hàm số y=f(x)
Đồ thị hàm số lẻ luôn nhận gốc tọa độ là tâm đối xứng.
Vậy để chứng minh là tâm đối xứng, ta dùng công thức đổi trục: để đưa hệ trục về hệ trục (gốc ) và chứng minh: trong hệ trục , hàm số đã cho có dạng là hàm số lẻ.
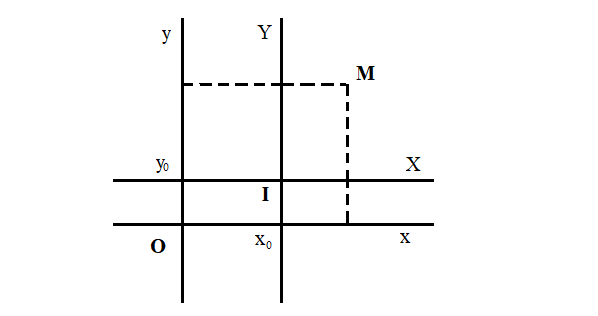
Chú ý:
2. Chứng minh đường thẳng là trục đối xứng của đồ thị (C) của hàm số y=f(x)
Đồ thị của hàm số chẵn luôn nhận trục tung là trục đối xứng. Vậy để chứng minh đường thẳng là trục đối xứng, ta dùng công thức đổi trục để đưa hệ số về hệ trục ( là trục tung) và chứng minh: trong hệ trục , hàm số đã cho có dạng là hàm số chẵn.
Sơ đồ tư duy về khảo sát sự biến thiên và vẽ đồ thị hàm số
Hàm số bậc ba:
có hai nghiệm phân biệt có cực trị.
vô nghiệm hoặc có nghiệm kép không có cực trị.
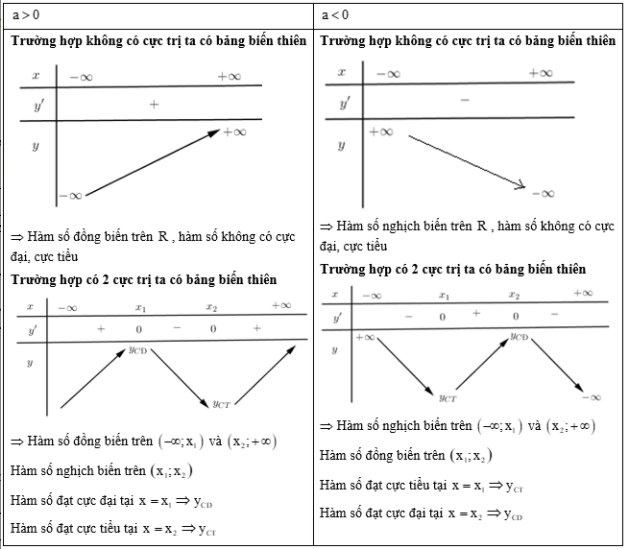

- Điểm uốn với là nghiệm của phương trình và .
TH1: có hai nghiệm phân biệt
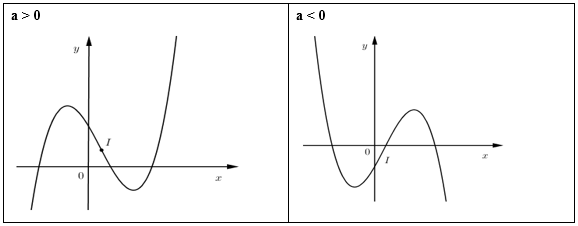

TH2: có nghiệm kép
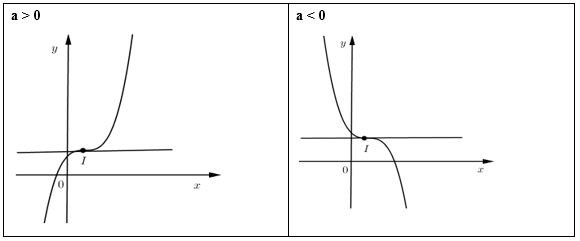

TH3: vô nghiệm
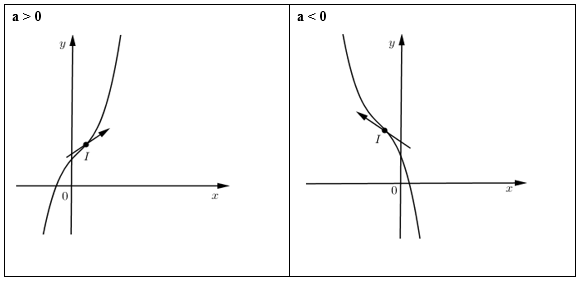
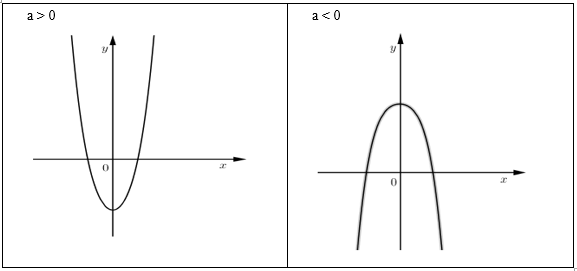
Hàm số bậc bốn trùng phương
+) TXĐ:
+) Sự biến thiên:
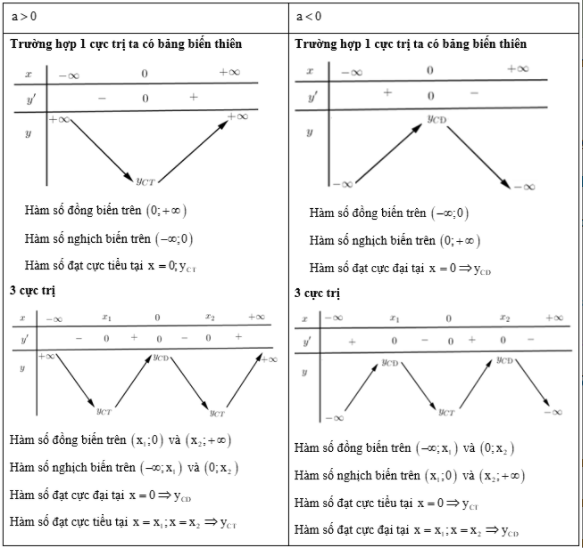

TH1: có 3 nghiệm phân biệt
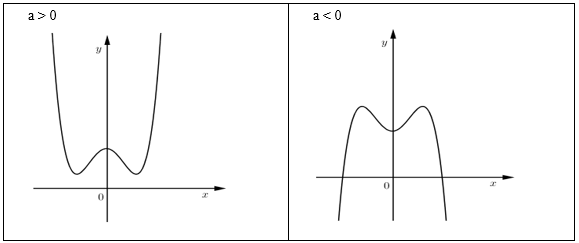

1. Kiến thức cần nhớ
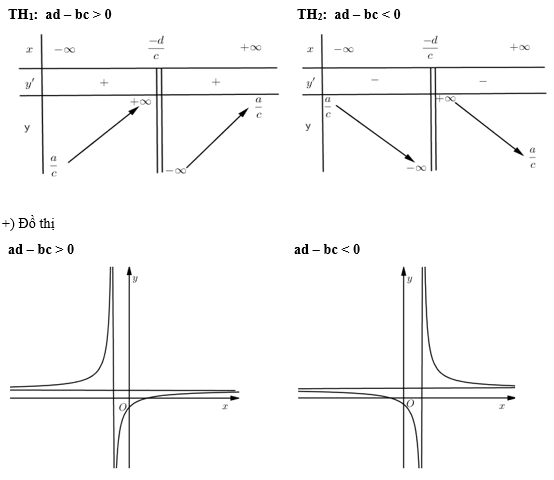
Cho hàm số
* Tập xác định
* Sự biến thiên
+)
+) Đường tiệm cận: tiệm cận đứng ; tiệm cận ngang .
+) Tâm đối xứng .
+) Bảng biến thiên :

2. Các dạng toán thường gặp
Phương pháp:
- Bước 1: Tìm các tiệm cận đứng, tiệm cận ngang của đồ thị hàm số đã cho.
+ Tiệm cận đứng là đường thẳng song song với trục , khi đó là nghiệm của mẫu thức.
+ Tiệm cận ngang là đường thẳng song song với trục , khi đó .
- Bước 2: Tìm giao điểm của đồ thị hàm số với hai trục tọa độ.
+ Giao điểm của đồ thị với trục là .
+ Giao điểm của đồ thị với trục là .
- Bước 3: Xét tính đơn điệu của hàm số.
+ Hai nhánh đồ thị hướng lên từ trái qua phải thì hàm số đồng biến .
+ Hai nhánh đồ thị hướng xuống từ trái qua phải thì hàm số nghịch biến .
Khi thực hành, HS có thể áp dụng từng bước để loại trừ đáp án, đến khi chọn được đáp án đúng thì kết luận, không nhất thiết phải thực hiện cả 3 bước nếu đã có được đáp án.
Phương pháp:
- Bước 1: Tìm các tiệm cận của đồ thị hàm số.
+ Tại điểm mà hoặc thì là tiệm cận đứng của đồ thị hàm số, khi đó là nghiệm của mẫu thức.
+ Nếu có tại điểm thì là tiệm cận ngang của đồ thị hàm số, khi đó .
- Bước 2: Xét tính đơn điệu của hàm số.
+ Nếu trên cả 2 khoảng và , đạo hàm đều mang dấu thì hàm số đồng biến trên 2 khoảng đó, khi đó .
+ Nếu trên cả 2 khoảng và , đạo hàm đều mang dấu thì hàm số nghịch biến trên 2 khoảng đó, khi đó .
Dạng 1: Tìm hàm số có đồ thị cho trước
Phương pháp:
- Bước 1: Nhận dạng đồ thị: Đồ thị thuộc dạng bậc 3 hay bậc 4, hệ số dương hay âm.
- Bước 2: Tìm điểm giao của đồ thị hàm số với và thay tọa độ vào các hàm số ở từng đáp án.
- Bước 3: Tìm các điểm cực đại, cực tiểu của đồ thị hàm số đã cho.
- Bước 4: Tính đạo hàm các hàm số ở mỗi đáp án và giải phương trình , tìm điểm cực đại, cực tiểu của đồ thị hàm số ở các đáp án.
- Bước 5: Giải phương trình ở các đáp án và tìm nghiệm, đối chiếu với hoành độ giao điểm của đồ thị hàm số đã cho với trục hoành.
Ví dụ 1:
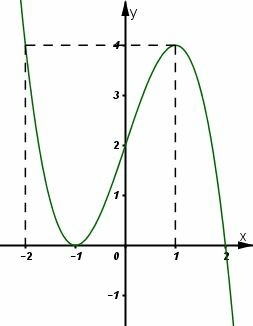
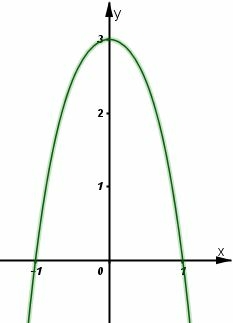
Đường cong trong hình vẽ bên là đồ thị của hàm số nào?
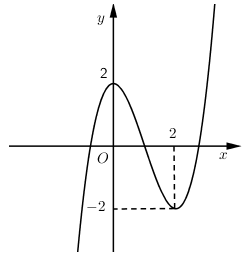
A. B.
C. D.
Cách giải:
Nhận xét: Đường cong trong hình vẽ là đồ thị của hàm số bậc 3 có hệ số a > 0
Loại đáp án A, C
Xét 2 đáp án B và D
Thay thì cả 2 đáp án B, D đều thỏa mãn
Thay chỉ có đáp án B thỏa mãn
Chọn B
HS chỉ cần thực hiện từng bước rồi loại bớt đáp án, đến khi chọn được đáp án đúng thì dừng lại, không nhất thiết phải thực hiện hết cả 5 bước nếu đã tìm ra đáp án trước đó để tránh mất thời gian.
Dạng 2: Tìm hàm số có bảng biến thiên cho trước
Phương pháp:
- Bước 1: Nhận dạng bảng biến thiên: Bảng biến thiên đã cho là của hàm bậc 3 hay bậc 4, hệ số âm hay dương.
- Bước 2: Tìm các điểm cực đại, cực tiểu của đồ thị hàm số dựa vào bảng biến thiên.
- Bước 3: Tính đạo hàm các hàm số ở mỗi đáp án và giải phương trình , tìm điểm cực đại, cực tiểu của đồ thị hàm số ở các đáp án.
Ví dụ 2:
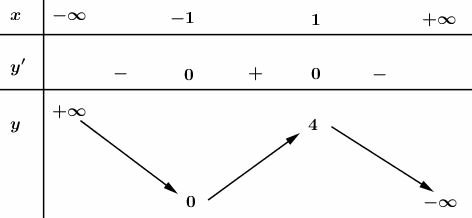
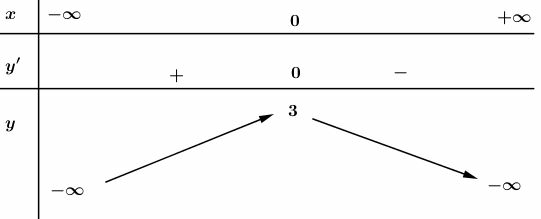
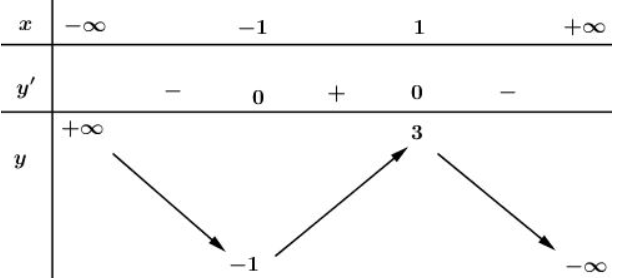
Cho hàm số xác định, liên tục trên R có bảng biến thiên:
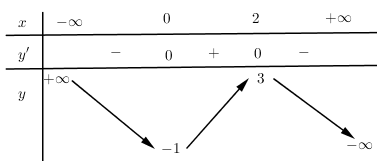
Bảng biến thiên trên là bảng biến thiên của hàm số nào?
A.
B.
C.
D.
Cách giải:
Nhận xét: Dễ thấy bảng biến thiên của đồ thị hàm số bậc 3 Þ Loại đáp án B
Ngoài cùng bên phải của Þ Loại đáp án A
Thay lần lượt hai điểm và vào 2 hàm số còn lại
Thay vào cả hai hàm số và ta thu được
đều thuộc vào 2 đồ thị hàm số và
Thay vào hàm số ta được y = 3
thuộc vào đồ thị hàm số
Thay vào hàm số ta được
không thuộc vào đồ thị hàm số
Chọn C
Dạng 3: Nhận xét các tính chất của hàm số, đồ thị hàm số có bảng biến thiên cho trước (về tính đơn điệu, cực trị, tâm đối xứng, trục đối xứng,…)
Phương pháp:
- Bước 1: Quan sát bảng biến thiên, tìm các khoảng đơn điệu, các điểm cực trị của hàm số.
- Bước 2: Nhận dạng bảng biến thiên: Bảng biến thiên đã cho là của hàm bậc 3 hay bậc 4, từ đó tìm được tâm đối xứng, trục đối xứng,...
- Bước 3: Đối chiếu các kết quả thu được ở trên với các đáp án bài cho và xét tính đúng sai của các đáp án.
Ví dụ 3:
Cho hàm số xác định liên tục trên R có bảng biến thiên:
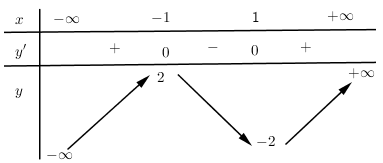
Khẳng định nào sau đây là đúng?
A. Hàm số có giá trị lớn nhất bằng 2
B. Điểm cực đại của đồ thị hàm số là
C. Cực tiểu của hàm số là
D. Điểm cực đại của đồ thị hàm số là
Cách giải:
Từ bảng biến thiên ta thấy:
- Hàm số không có GTLN nên A sai.
- Điểm cực đại của đồ thị hàm số là nên D sai, là điểm cực đại của hàm số nên B sai.
- Giá trị cực tiểu của hàm số là nên C đúng.
Chọn C
HS cũng có thể xét tính đúng sai của từng đáp án ngay mà không cần nhận xét tất cả các tính chất của hàm số, đồ thị hàm số đã nêu ở trên để tránh mất nhiều thời gian.
Dạng 4: Tìm điều kiện của các hệ số của hàm đa thức bậc ba có đồ thị cho trước
Cho hàm số có đồ thị cho trước. Tìm điều kiện của .
Phương pháp:
- Bước 1: Xét tính dương, âm của hệ số dựa và dáng đồ thị.
- Bước 2: Tìm điều kiện của dựa và giao điểm của đồ thị hàm số với trục .
+ Nếu giao điểm nằm trên trục hoành thì .
+ Nếu giao điểm nằm dưới trục hoành thì .
+ Nếu giao điểm trùng với gốc tọa độ thì .
- Bước 3: Tìm điều kiện của dựa vào các điểm cực trị của đồ thị hàm số:
+ Nếu đồ thị hàm số không có cực trị thì phương trình vô nghiệm hoặc có nghiệm kép .
+ Nếu đồ thị hàm số có hai cực trị thì phương trình có hai nghiệm phân biệt .
+ Nếu đồ thị hàm số có hai cực trị nằm trái phía với trục tung thì phương trình có hai nghiệm phân biệt trái dấu .
+ Nếu đồ thị hàm số có hai cực trị cùng nằm bên trái trục tung thì phương trình có hai nghiệm phân biệt cùng âm
+ Nếu đồ thị hàm số có hai cực trị cùng nằm bên phải trục tung thì phương trình có hai nghiệm phân biệt cùng dương
Ví dụ 4:
Cho hàm sốcó đồ thị hàm số như hình vẽ dưới đây. Khẳng định nào sau đây về dấu củalà đúng nhất?
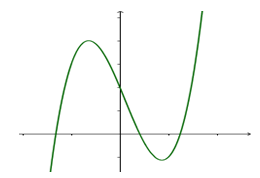
A. B.
C. D.
Cách giải
nên
Dựa vào đồ thị hàm số ta có có hai nghiệm phân biệt trái dấu
mà nên suy ra suy ra loại B, C.
Mặt khác thấy đồ thị cắt trục oy tại điểm có tung độ dương
Chọn D
Dạng 5: Tìm điều kiện của tham số để đồ thị hàm số có điểm uốn thỏa mãn điều kiện cho trước
Phương pháp:
- Bước 1: Tính , giải phương trình .
- Bước 2: Giả sử là một nghiệm của phương trình thì điểm uốn .
- Bước 3: Thay tọa độ điểm uốn vào điều kiện đề bài để tìm

