Chúng tôi giới thiệu Giải bài tập Toán lớp 12 Bài 2: Cực trị của hàm số chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Cực trị của hàm số lớp 12.
Bài giảng Toán học 12 Bài 2: Cực trị của hàm số
Giải bài tập Toán lớp 12 Bài 2: Cực trị của hàm số
Trả lời câu hỏi giữa bài
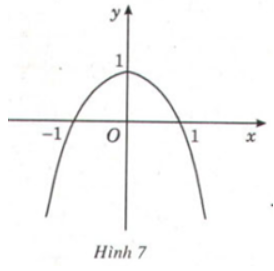
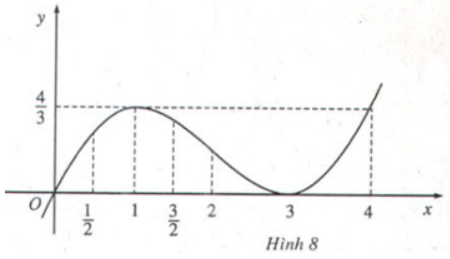
Phương pháp giải:
Quan sát đồ thị hàm số và xét trong từng khoảng, tìm điểm cao nhất (ứng với giá trị lớn nhất) và điểm thấp nhất (ứng với giá trị nhỏ nhất).
Lời giải:
a)
Từ đồ thị hàm số ta thấy, tại hàm số có giá trị lớn nhất bằng .
Xét dấu đạo hàm:

b)
Từ đồ thị hàm số ta thấy:
Tại hàm số có giá trị lớn nhất bằng
Tại hàm số có giá trị nhỏ nhất bằng .
Xét dấu đạo hàm:
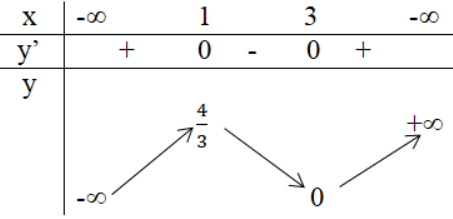
Phương pháp giải:
Lời giải:
- Với
Ta có
- Với
Ta có
Do đó
Trả lời câu hỏi 3 trang 14 SGK Giải tích 12: a) Sử dụng đồ thị, hãy xem xét các hàm số sau đây có cực trị hay không
b) Nêu mối quan hệ giữa sự tồn tại cực trị và dấu của đạo hàm.
Phương pháp giải:
Quan sát đồ thị, tìm điểm cực trị (cực đại: điểm mà tại đó hàm số chuyển từ đồng biến sang nghịch biến, cực tiểu: ngược lại)
Lời giải:
a)
Hàm số không có cực trị.
Hàm số đạt cực đại tại và đạt cực tiểu tại
b)Phương pháp giải:
+ Hàm số k có đạo hàm:
+ Hàm số có cực trị: quan sát từ đồ thị
Lời giải:
Khi đó:
Ta có:
Vậy không tồn tại đạo hàm của hàm số tại
Nhưng dựa vào đồ thị của hàm số Ta có hàm số đạt cực trị tại
Lời giải:
1. TXĐ:
2. . Cho hoặc
3. Ta có bảng biến thiên:

Hàm số đạt cực đại tại và giá trị cực đại là
Hàm số đạt cực tiểu tại và giá trị cực tiểu là
a) ;
b) ;
c)
d) ;
e)
Phương pháp giải:
Quy tắc 1 tìm cực trị của hàm số:
Bước 1: Tìm tập xác định.
Bước 2: Tính . Tìm các điểm mà tại đó bằng 0 hoặc không xác định.
Bước 3: Lập bảng biến thiên.
Bước 4: Từ bảng biến thiên suy ra các điểm cực trị.
Lời giải:
a)
Tập xác định:
Bảng biến thiên:
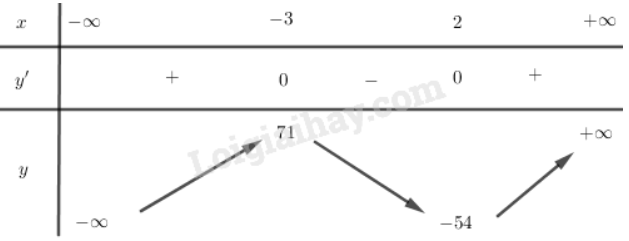
Hàm số đạt cực đại tại và CĐ
Hàm số đạt cực tiểu tại và CT
b)
Tập xác định:
;
Bảng biến thiên:
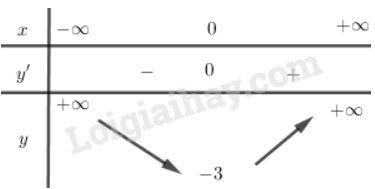
Hàm số đạt cực tiểu tại và CT
c)
Tập xác định: \ { 0 }
Bảng biến thiên
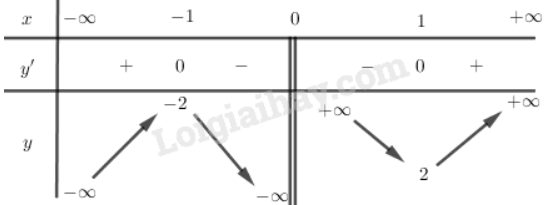
Hàm số đạt cực đại tại , CĐ
Hàm số đạt cực tiểu tại , CT
d)
Tập xác định
Bảng biến thiên:
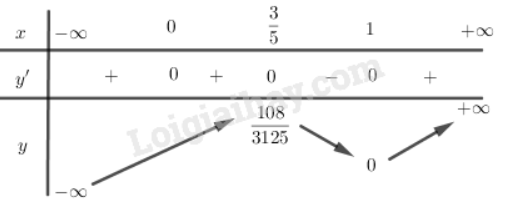
Hàm số đạt cực đại tại
Hàm số đạt cực tiểu tại , CT =
e)
Vì – nên tập xác định :
Bảng biến thiên:
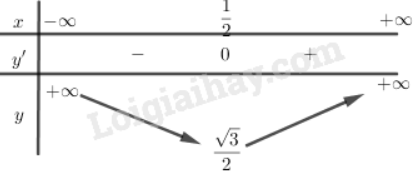
Hàm số đạt cực tiểu tại
a) ;
b) ;
c) ;
d) .
Phương pháp giải:
Quy tắc II tìm cực trị của hàm số.
Bước 1: Tìm tập xác định.
Bước 2: Tính . Giải phương trình và kí hiệu là các nghiệm của nó.
và .
Bước 4: Dựa vào dấu của suy ra tính chất cực trị của điểm xi.
Lời giải:
a)
TXĐ:
;
.
.
nên hàm số đạt cực đại tại ,
CĐ = .
nên hàm số đạt cực tiểu tại ,
CT = = 0.
b)
TXĐ:
;
.
nên hàm số đạt cực đại tại các điểm ,
CĐ = = , .
nên hàm số đạt cực tiểu tại các điểm ,
CT = = , .
c)
TXĐ:
;
;
Do đó hàm số đạt cực đại tại các điểm ,
đạt cực tiểu tại các điểm
d)
TXĐ:
; .
.
nên hàm số đạt cực tiểu tại ,
CT = .
hàm số đạt cực đại tại ,
CĐ = .
Bài 3 trang 18 SGK Giải tích 12: Chứng minh rằng hàm số không có đạo hàm tại nhưng vẫn đạt cực tiểu tại điểm đó.
Phương pháp giải:
- Tính giới hạn trái, giới hạn phải của khi , từ đó suy ra không tồn tại đạo hàm tại .
- Chứng minh với mọi .
Lời giải:
Ta có:
Không tồn tại đạo hàm của hàm số đã cho tại .
Dễ thấy với mọi và nên chính là điểm cực tiểu của hàm số.
luôn luôn có một điểm cực đại và một điểm cực tiểu.
Phương pháp giải:
B1: Tính
B2: Chứng tỏ phương trình luôn có 2 nghiệm phân biệt, với mọi m
Từ đó suy ra dấy của và sự tồn tại cực đại cực tiểu.
Lời giải:
TXĐ:
Ta có:
Xét phương trình:
Có:
phương trình luôn có hai nghiệm phân biệt .
Giả sử , ta có bảng biến thiên:
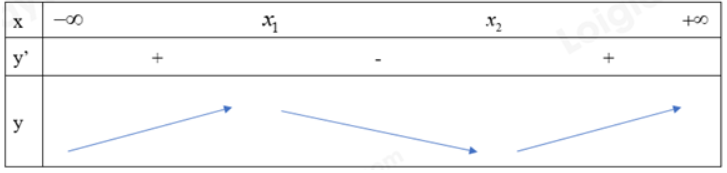
Dễ thấy hàm số đạt cực đại tại và đạt cực tiểu tại .
Vậy hàm số luôn có một cực đại và một cực tiểu.
đều là những số dương và là điểm cực đại.
Phương pháp giải:
- Hàm số đã cho đạt cực đại tại , từ đó tìm .
- Thay vừa tìm được ở trên vào hàm số.
Tìm dựa vào điều kiện: Hàm số đã cho có các cực trị đều dương .
Lời giải:
Ta có: , .
Hàm số đã cho đạt cực đại tại
Ta có: có với nên phương trình luôn có hai nghiệm phân biệt.
Hàm số đã cho có các cực trị đều dương .
Với thì .
Do đó
Với thì .
Do đó
.
Vậy các giá trị cần tìm là: hoặc .
Phương pháp giải:
Vận dụng kiến thức:
là điểm cực đại của hàm số
Lời giải:
Tập xác định:
Ta có: .
Hàm số đạt cực đại tại
+)
+)
Vậy .
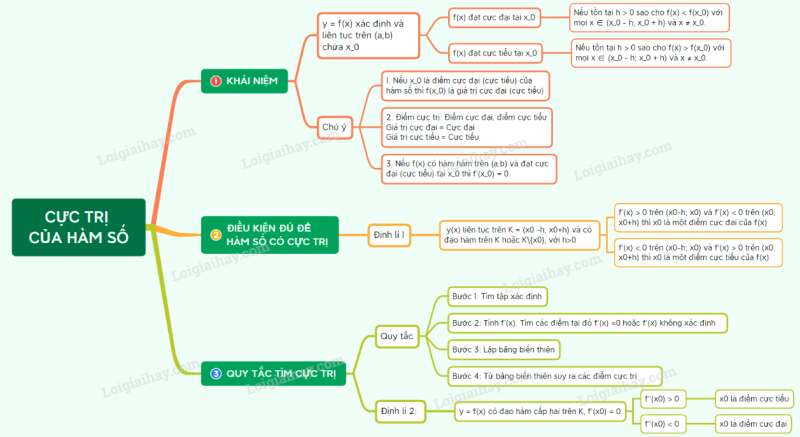
1. Định nghĩa
Cho hàm số liên tục trên khoảng và điểm
- Nếu tồn tại số sao cho thì ta nói hàm số đạt cực đại tại
- Nếu tồn tại số sao cho thì ta nói hàm số đạt cực tiểu tại
Chú ý:
a) Cần phân biệt các các khái niệm:
- Điểm cực trị của hàm số.
- Giá trị cực trị của hàm số.
- Điểm cực trị của đồ thị hàm số.
b) Nếu có đạo hàm trên và đạt cực trị tại thì .
2. Điều kiện đủ để hàm số có cực trị
Định lí 1. Cho hàm số liên tục trên khoảng và có đạo hàm trên hoặc trên
+) Nếu thì là điểm cực đại của hàm số
+) Nếu thì là điểm cực tiểu của hàm số
Hàm số có thể đạt cực trị tại những điểm mà tại đó đạo hàm không xác định.

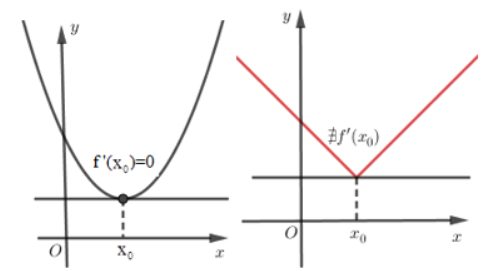
Giả sử có đạo hàm cấp 2 trong .
a) Nếu thì là một điểm cực tiểu của hàm số.
b) Nếu thì là một điểm cực đại của hàm số.
3. Quy tắc tìm cực trị của hàm số
Phương pháp:
Có thể tìm cực trị của hàm số bởi một trong hai quy tắc sau:
- Bước 1: Tìm tập xác định của hàm số.
- Bước 2: Tính , tìm các điểm tại đó hoặc không xác định.
- Bước 3: Lập bảng biến thiên và kết luận.
+ Tại các điểm mà đạo hàm đổi dấu từ âm sang dương thì đó là điểm cực tiểu của hàm số.
+ Tại các điểm mà đạo hàm đổi dấu từ dương sang âm thì đó là điểm cực đại của hàm số.
- Bước 1: Tìm tập xác định của hàm số.
- Bước 2: Tính , giải phương trình và kí hiệu là các nghiệm của nó.
- Bước 3: Tính và .
- Bước 4: Dựa và dấu của suy ra điểm cực đại, cực tiểu:
+ Tại các điểm mà thì đó là điểm cực tiểu của hàm số.
+ Tại các điểm mà thì đó là điểm cực đại của hàm số.
Sơ đồ tư duy về cực trị của hàm số
Dạng 1: Tìm điều kiện của tham số để hàm số bậc ba có điểm cực trị
Phương pháp:
- Bước 1: Tính .
- Bước 2: Nêu điều kiện để hàm số bậc ba có điểm cực trị:
+ Hàm số có điểm cực trị có hai nghiệm phân biệt .
+ Hàm số không có điểm cực trị vô nghiệm hoặc có nghiệm kép .
- Bước 3: Kết luận.
Hàm số bậc ba chỉ có thể có hai cực trị hoặc không có cực trị nào.
Phương pháp:
- Bước 1: Tính .
- Bước 2: Nêu điều kiện để hàm số có điểm cực trị:
+ Hàm số có điểm cực trị nếu phương trình có nghiệm duy nhất.
+ Hàm số có điểm cực trị nếu phương trình có ba nghiệm phân biệt.
- Bước 3: Kết luận.
Hàm số bậc bốn trùng phương chỉ có thể có điểm cực trị hoặc có điểm cực trị.
+ Trường hợp có điểm cực trị thì đó là .
+ Trường hợp có điểm cực trị thì đó là
Phương pháp:
- Bước 1: Tính .
- Bước 2: Nêu điều kiện để là điểm cực trị của hàm số:
+ là điểm cực đại nếu
+ là điểm cực tiểu nếu
- Bước 3: Kết luận.
- Bước 1: Tính .
- Bước 2: Nêu điều kiện để đồ thị hàm số có 2 điểm cực trị thỏa mãn điều kiện:
+ Đồ thị hàm số có 2 điểm cực trị nằm về hai phía trục tung
có hai nghiệm phân biệt trái dấu
+ Đồ thị hàm số có 2 điểm cực trị nằm cùng phía so với trục tung
có hai nghiệm phân biệt cùng dấu
+ Đồ thị hàm số có 2 điểm cực trị nằm về bên phải trục tung
có hai nghiệm phân biệt cùng dương
+ Đồ thị hàm số có 2 điểm cực trị nằm về bên trái trục tung
có hai nghiệm phân biệt cùng âm
+ Đồ thị hàm số có 2 điểm cực trị thỏa mãn đẳng thức liên hệ giữa thì ta biến đổi đẳng thức đã cho làm xuất hiện rồi sử dụng hệ thức Vi-et để thay và tìm .
Phương pháp:
- Bước 1: Tính .
- Bước 2: Nêu điều kiện để đồ thị hàm số có ba điểm cực trị thỏa mãn điều kiện:
+ Ba điểm cực trị trong đó lập thành một tam giác vuông (vuông cân)
vuông tại .
Khi đó:
Đây là công thức tính nhanh trong bài toán trắc nghiệm.
+ Ba điểm cực trị trong đó tạo thành tam giác đều .
+ Ba điểm cực trị trong đó tạo thành tam giác có diện tích cho trước
với là trung điểm của .
+ Ba điểm cực trị trong đó tạo thành tam giác có diện tích lớn nhất
Tìm với là trung điểm của .
+ Ba điểm cực trị trong đó tạo thành tam giác cân có góc ở đỉnh bằng cho trước
+ Ba điểm cực trị trong đó tạo thành tam giác có ba góc nhọn
là góc ở đỉnh phải nhọn
- Bước 3: Kết luận.
Phương pháp:
- Bước 1: Tính .
- Bước 2: Lấy chia ta được đa thức dư .
- Bước 3: Kết luận: là đường thẳng cần tìm.

