Cho hình vuông ABCD cạnh a, tâm O. Khi đó: |→OA+→OB|=

Dựng hình bình hành OAEB và gọi M là giao điểm của AB và OE.
Ta có: |→OA+→OB|=|→OE|=OE=2OM=a
Cho tam giác ABC, trọng tâm là G. Phát biểu nào là đúng?
Ta có: |→GA−→BG−→CG|=|→GA+→GB+→GC|=|→0|=0.
Cho lục giác đềuABCDEF và O là tâm của nó. Đẳng thức nào dưới đây là đẳng thức sai?
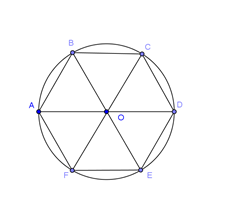
→AB+→CD+→FE=→AB+→BO+→FE=→AO+→OD=→AD≠→0.
Cho tam giác ABC. Để điểm M thoả mãn điều kiện →MA−→MB+→MC=→0 thì M phải thỏa mãn mệnh đề nào?
Ta có: →MA−→MB+→MC=→0⇔→BA+→MC=→0⇔→MC=→AB
Vậy: M là điểm sao cho tứ giác BAMClà hình bình hành.
Cho ΔABC vuông tại A và AB=3, AC=4. Véctơ →CB+→AB có độ dài bằng
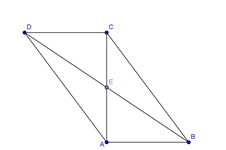
Dựng hình bình hành ABCD tâm E
Ta có: →CB+→AB=→DA+→DC=→DB
⇒|→CB+→AB|=|→DB|=DB=2EB=2√AE2+AB2=2√13
Cho tam giác ABC. Để điểm M thoả mãn điều kiện →MA+→BM+→MC=→0 thì M phải thỏa mãn mệnh đề nào?
→MA+→BM+→MC=→0⇔→MA+→BC=→0⇔→BC=→AM
Vậy M là điểm sao cho tứ giác BAMClà hình bình hành.
Cho lục giác đều ABCDEF và O là tâm của nó. Đẳng thức nào dưới đây là đẳng thức sai?
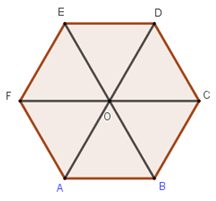
Ta có:
→OA+→OC−→EO=→OB+→OE=→0⇒Ađúng→BC−→EF=→BC+→FE=→AO+→OD=→AD⇒Bđúng→OA−→OE=→EA→EB−→OC=→EB+→CO=→EB+→BA=→EA⇒→OA−→OE=→EB−→OC⇒Cđúng
→AB+→CD−→EF=→AB+→BO−→OA
=→AO−→OA=2→AO≠→0
Hay D sai.
Cho hình thang ABCD có AB song song với CD. Cho AB=2a;CD=a. Gọi O là trung điểm của AD. Khi đó :
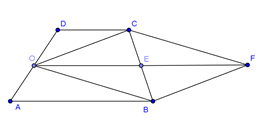
Dựng hình bình hành OBFC tâm E. Khi đó
|→OB+→OC|=|→OF|=OF=2OE=AB+CD=3a.
Cho tam giác ABC. Tập hợp những điểm M sao cho: |→MA+→MB|=|→MC+→MB| là:
GọiI,J lần lượt là trung điểm của AB vàBC. Khi đó:
|→MA+→MB|=|→MC+→MB|⇔2|→MI|=2|→MJ|⇔MI=MJ
Vậy M nằm trên đường trung trực của IJ.
Chú ý khi giải:
Một số em có thể sẽ chọn nhầm đáp án A sau khi có đẳng thức độ dài MI=MJ là sai.

