Cho lục giác đều $ABCDEF$ và $O$ là tâm của nó. Đẳng thức nào dưới đây là đẳng thức sai?
Trả lời bởi giáo viên
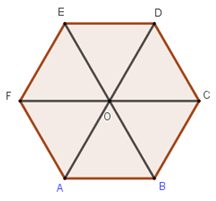
Ta có:
$\begin{array}{l}
\overrightarrow {OA} + \overrightarrow {OC} - \overrightarrow {EO} = \overrightarrow {OB} + \overrightarrow {OE} = \overrightarrow 0 \\
\Rightarrow A\,\,\text{đúng}\\
\overrightarrow {BC} - \overrightarrow {EF} = \overrightarrow {BC} + \overrightarrow {FE} = \overrightarrow {AO} + \overrightarrow {OD} = \overrightarrow {AD} \\
\Rightarrow B\,\,\text{đúng}\\
\overrightarrow {OA} - \overrightarrow {OE} = \overrightarrow {EA} \\
\overrightarrow {EB} - \overrightarrow {OC} = \overrightarrow {EB} + \overrightarrow {CO} = \overrightarrow {EB} + \overrightarrow {BA} = \overrightarrow {EA} \\
\Rightarrow \overrightarrow {OA} - \overrightarrow {OE} = \overrightarrow {EB} - \overrightarrow {OC} \\
\Rightarrow C\,\,\text{đúng}
\end{array}$
$\overrightarrow {AB} + \overrightarrow {CD} - \overrightarrow {EF} = \overrightarrow {AB} + \overrightarrow {BO} - \overrightarrow {OA} $
$ = \overrightarrow {AO} - \overrightarrow {OA} = 2\overrightarrow {AO} \ne \overrightarrow 0 $
Hay D sai.
Hướng dẫn giải:
Sử dụng tính chất hình lục giác đều, tìm các véc tơ bằng nhau trong hình và quy tắc trừ hai véc tơ để kết luận.

