Cho \(A\left( {0;3} \right),\,B\left( {4;2} \right)\). Điểm \(D\) thỏa $\overrightarrow {OD} + 2\overrightarrow {DA} - 2\overrightarrow {DB} = \overrightarrow 0 $, tọa độ \(D\) là:
Ta có: $\overrightarrow {OD} + 2\overrightarrow {DA} - 2\overrightarrow {DB} = \overrightarrow 0 \Leftrightarrow \left\{ \begin{array}{l}{x_D} - 0 + 2\left( {0 - {x_D}} \right) - 2\left( {4 - {x_D}} \right) = 0\\{y_D} - 0 + 2\left( {3 - {y_D}} \right) - 2\left( {2 - {y_D}} \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 8\\{y_D} = - 2\end{array} \right.$.
Cho hình vuông \(ABCD\) cạnh \(a\). Hỏi mệnh đề nào sau đây sai?
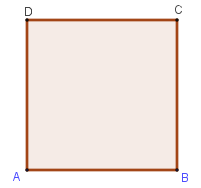
Phương án A: Do \(\overrightarrow {DA} .\overrightarrow {CB} = DA.CB.\cos {0^0} = {a^2}\) nên loại A đúng, loại A.
Phương án B: Do \(\overrightarrow {AB} .\overrightarrow {CD} = AB.CD.\cos {180^{\rm{o}}} = - {a^2}\) nên B đúng, loại B.
Phương án C: \(\left( {\overrightarrow {AB} + \overrightarrow {BC} } \right).\overrightarrow {AC} = \overrightarrow {AC} .\overrightarrow {AC} = A{C^2} = {\left( {a\sqrt 2 } \right)^2} = 2{a^2}\) nên C sai, chọn C.
Phương án D: \(\overrightarrow {AB} .\overrightarrow {AD} + \overrightarrow {CB} .\overrightarrow {CD} = 0\) đúng vì \(AB \bot AD,CB \bot CD\)
Tam giác \(ABC\) có \(C\left( { - 2; - 4} \right)\), trọng tâm \(G\left( {0;4} \right)\), trung điểm cạnh \(BC\) là \(M\left( {2;0} \right)\). Tọa độ \(A\) và \(B\) là:
Ta có: \(M\left( {2;0} \right)\) là trung điểm \(BC\) nên \(\left\{ \begin{array}{l}2 = \dfrac{{{x_B} + ( - 2)}}{2}\\0 = \dfrac{{{y_B} + ( - 4)}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} = 6\\{y_B} = 4\end{array} \right. \Rightarrow B\left( {6;4} \right)\)
\(G\left( {0;4} \right)\)là trọng tâm tam giác \(ABC\) nên $\left\{ \begin{array}{l}0 = \dfrac{{{x_A} + 6 + ( - 2)}}{3}\\4 = \dfrac{{{y_A} + 4 + ( - 4)}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_A} = - 4\\{y_A} = 12\end{array} \right. \Rightarrow A\left( { - 4;12} \right)$
Cho $\overrightarrow a = 3\overrightarrow i - 4\overrightarrow j $ và $\overrightarrow b = \overrightarrow i - \overrightarrow j $. Tìm phát biểu sai:
Ta có: $\overrightarrow a = 3\overrightarrow i - 4\overrightarrow j \Rightarrow \overrightarrow a \left( {3; - 4} \right)$ $ \Rightarrow \left| {\overrightarrow a } \right| = \sqrt {{3^2} + {{\left( { - 4} \right)}^2}} = 5$ nên A đúng.
$\overrightarrow b = \overrightarrow i - \overrightarrow j \Rightarrow \overrightarrow b \left( {1; - 1} \right) $ $\Rightarrow \left| {\overrightarrow b } \right| = \sqrt {{1^2} + {{\left( { - 1} \right)}^2}} = \sqrt 2 $ nên D đúng, B sai.
Ngoài ra $\overrightarrow a - \overrightarrow b = \left( {2; - 3} \right)$ nên C đúng.
Trong mặt phẳng $Oxy$, cho $B\left( {5; - 4} \right),C\left( {3;7} \right)$. Tọa độ của điểm $E$ đối xứng với $C$ qua $B$ là
Ta có: $E$ đối xứng với $C$ qua $B \Leftrightarrow B$ là trung điểm đoạn thẳng $EC$
Do đó, ta có: $\left\{ \begin{array}{l}5 = \dfrac{{{x_E} + 3}}{2}\\ - 4 = \dfrac{{{y_E} + 7}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_E} = 7\\{y_E} = - 15\end{array} \right. \Rightarrow E\left( {7; - 15} \right)$
Cho $A\left( {1;2} \right),\,B\left( { - 2;6} \right)$. Điểm $M$ trên trục $Oy$ sao cho ba điểm $A,B,M$ thẳng hàng thì tọa độ điểm $M$ là:
Ta có: $M$ trên trục $Oy \Rightarrow M\left( {0;y} \right)$
Ba điểm $A,B,M$ thẳng hàng khi $\overrightarrow {AB} $ cùng phương với $\overrightarrow {AM} $
Ta có $\overrightarrow {AB} = \left( { - 3;4} \right),\,\,\overrightarrow {AM} = \left( { - 1;y - 2} \right)$.
Do đó, $\overrightarrow {AB} $ cùng phương với $\overrightarrow {AM} \Leftrightarrow \dfrac{{ - 1}}{{ - 3}} = \dfrac{{y - 2}}{4} \Rightarrow y = \dfrac{{10}}{3}$.
Vậy $M\left( {0;\dfrac{{10}}{3}} \right)$
Trong mặt phẳng $Oxy$, gọi $B',B''$ và $B'''$ lần lượt là điểm đối xứng của $B\left( { - 2;7} \right)$ qua trục $Ox$,$Oy$ và qua gốc tọa độ $O$. Tọa độ của các điểm $B',\,B''$ và $B'''$ là:
Ta có:
$B'$ đối xứng với $B\left( { - 2;7} \right)$ qua trục $Ox \Rightarrow B'\left( { - 2; - 7} \right)$.
$B''$ đối xứng với $B\left( { - 2;7} \right)$ qua trục $Oy \Rightarrow B''\left( {2;7} \right)$.
$B'''$ đối xứng với $B\left( { - 2;7} \right)$ qua gốc tọa độ $O \Rightarrow B'''\left( {2; - 7} \right)$.
Cho \(K\left( {1; - 3} \right)\). Điểm \(A \in Ox,B \in Oy\) sao cho \(A\) là trung điểm \(KB\). Tọa độ điểm \(B\) là:
Ta có: \(A \in Ox,B \in Oy \Rightarrow A\left( {x;0} \right),B\left( {0;y} \right)\)
\(A\) là trung điểm $KB \Rightarrow \left\{ \begin{array}{l}x = \dfrac{{1 + 0}}{2}\\0 = \dfrac{{ - 3 + y}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{1}{2}\\y = 3\end{array} \right.$.Vậy \(B\left( {0;3} \right)\).
Trong mặt phẳng tọa độ \(Oxy\), cho tam giác \(MNP\) có \(M\left( {1; - 1} \right),\,N\left( {5; - 3} \right)\) và \(P\) thuộc trục \(Oy\),trọng tâm \(G\) của tam giác nằm trên trục \(Ox\).Toạ độ của điểm \(P\) là
Ta có: \(P\) thuộc trục \(Oy \Rightarrow P\left( {0;y} \right)\), \(G\) nằm trên trục \(Ox \Rightarrow G\left( {x;0} \right)\)
\(G\) là trọng tâm tam giác \(MNP\)nên ta có: \(\left\{ \begin{array}{l}x = \dfrac{{1 + 5 + 0}}{3}\\0 = \dfrac{{( - 1) + ( - 3) + y}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 4\end{array} \right.\)
Vậy \(P\left( {0;4} \right)\).
