Số phức, các phép toán với số phức
Kỳ thi ĐGNL ĐHQG Hồ Chí Minh
Cho \({z_1} = 2 + i;\,\,{z_2} = 1 - 3i.\) Tính \(A = {\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2}.\)
Ta có: \(\left\{ \begin{array}{l}{z_1} = 2 + i\\{z_2} = 1 - 3i\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{\left| {{z_1}} \right|^2} = {2^2} + 1 = 5\\{\left| {{z_2}} \right|^2} = 1 + {\left( { - 3} \right)^2} = 10\end{array} \right.\) \( \Rightarrow {\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2} = 15.\)
Cho số phức \(z = 3 - 4i\). Modun của \(z\) bằng
Modun của số phức \(z = 3 - 4i\) là: \(\left| z \right| = \sqrt {{3^2} + {{\left( { - 4} \right)}^2}} = 5.\)
Tính môđun của số phức \(w = {\left( {1 - i} \right)^2}z\), biết số phức z có môđun bằng m.
Ta có \(\left| w \right| = \left| {{{\left( {1 - i} \right)}^2}z} \right| = \left| {{{\left( {1 - i} \right)}^2}} \right|.\left| z \right| \)
\( = {\left| {1 - i} \right|^2}.\left| z \right| = {\left( {\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} } \right)^2}.\left| z \right|= 2\left| z \right| = 2m\) vì \(\left| z \right| = m\).
Cho hai số phức \({z_1},\,\,{z_2}\) thỏa mãn \({z_1}.\overline {{z_1}} = 4\), \(\left| {{z_2}} \right| = 3\). Giá trị biểu thức \(P = {\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2}\) bằng:
Ta có: \({z_1}.\overline {{z_1}} = 4 \Rightarrow {\left| {{z_1}} \right|^2} = 4\).
Vậy \(P = {\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2} = 4 + {3^2} = 13\).
Cho các số phức \({z_1} = 3i,{z_2} = m - 2i\). Số giá trị nguyên của m để \(\left| {{z_2}} \right| < \left| {{z_1}} \right|\) là
Ta có \({z_1} = 3i;\,\,{z_2} = m - 2i \Rightarrow \left\{ \begin{array}{l}\left| {{z_1}} \right| = 3\\\left| {{z_2}} \right| = \sqrt {{m^2} + 4} \end{array} \right.\)
Mà \(\left| {{z_2}} \right| < \left| {{z_1}} \right| \Rightarrow \sqrt {{m^2} + 4} < 3 \Leftrightarrow {m^2} + 4 < 9 \Leftrightarrow - \sqrt 5 < m < \sqrt 5 .\)
Mặt khác \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 2; - 1;0;1;2} \right\}.\)
Có 5 giá trị của m thỏa mãn yêu cầu bài toán.
Cho hai số phức \({z_1} = 1 + 2i\) và \({z_2} = 2 - 3i\). Phần ảo của số phức \(w = 3{z_1} - 2{z_2}\) là
Ta có \(\left\{ \begin{array}{l}{z_1} = 1 + 2i\\{z_2} = 2 - 3i\end{array} \right. \Rightarrow w = 3{z_1} - 2{z_2} = - 1 + 12i\)
Khi đó phần ảo của số phức w là 12.
Cho số phức $z = 1 + i + {i^2} + {i^3} + ... + {i^9}$. Khi đó:
$z = 1 + i + {i^2} + {i^3} + ... + {i^9} = 1 + i - 1 - i + 1 + i - 1 - i + 1 + i = 1 + i$
Có bao nhiêu số phức \(z = a + bi\) với \(a,\,\,b\) tự nhiên thuộc đoạn \(\left[ {2;9} \right]\) và tổng \(a + b\) chia hết cho 3?
Trong đoạn \(\left[ {2;9} \right]\) có
+) 3 số chia hết cho 3: \(\left\{ {3;6;9} \right\}\).
+) 2 số chia 3 dư 1: \(\left\{ {4;7} \right\}\).
+) 3 số chia 3 dư 2: \(\left\{ {2;5;8} \right\}\).
Để \(a + b\) chia hết cho 3 thì
+) Cả 2 số a, b khác nhau đều chia hết cho 3 có \(A_3^2 = 6\) số phức thỏa mãn.
+) Cả 2 số giống nhau đều chia hết cho 3 có 3 số phức thỏa mãn.
+) 1 số chia 3 dư 1 và 1 số chia 3 dư 2: Có \(C_2^1.C_3^1.2! = 12\) số phức thỏa mãn.
Vậy có tất cả 21 số phức thỏa mãn.
Có bao nhiêu số phức \(z\) thỏa mãn \(\left| z \right| = 1\) và \(\left| {{z^3} + 2024z + \overline z } \right| - 2\sqrt 3 \left| {z + \overline z } \right| = 2019\)?
Ta có :
\(\begin{array}{l}\left| {{z^3} + 2024z + \overline z } \right| - 2\sqrt 3 \left| {z + \overline z } \right| = 2019 \Leftrightarrow \dfrac{{\left| {{z^3} + 2024z + \overline z } \right|}}{{\left| z \right|}} - 2\sqrt 3 \left| {z + \overline z } \right| = 2019\\ \Leftrightarrow \left| {{z^2} + 2024 + \dfrac{{\overline z }}{z}} \right| - 2\sqrt 3 \left| {z + \overline z } \right| = 2019 \Leftrightarrow \left| {{z^2} + 2024 + {{\overline z }^2}} \right| - 2\sqrt 3 \left| {z + \overline z } \right| = 2019\\ \Leftrightarrow \left| {{{\left( {z + \overline z } \right)}^2} - 2z\overline z + 2024} \right| - 2\sqrt 3 \left| {z + \overline z } \right| = 2019 \Leftrightarrow \left| {{{\left( {z + \overline z } \right)}^2} + 2022} \right| - 2\sqrt 3 \left| {z + \overline z } \right| = 2019\end{array}\)
Đặt \(z = a + bi \Rightarrow \overline z = a - bi \Rightarrow z + \overline z = 2a\).
Khi đó phương trình cuối trở thành \(\left| {{{\left( {2a} \right)}^2} + 2022} \right| - 2\sqrt 3 .\left| {2a} \right| = 2019 \Leftrightarrow 4{a^2} - 4\sqrt 3 \left| a \right| + 3 = 0\)
\( \Leftrightarrow {\left( {2\left| a \right| - \sqrt 3 } \right)^2} = 0 \Leftrightarrow \left| a \right| = \dfrac{{\sqrt 3 }}{2} \Leftrightarrow a = \pm \dfrac{{\sqrt 3 }}{2}\).
Mà \(\left| z \right| = 1 \Leftrightarrow {\left| z \right|^2} = 1 \Leftrightarrow {a^2} + {b^2} = 1 \Rightarrow {b^2} = 1 - {a^2} = \dfrac{1}{4} \Leftrightarrow b = \pm \dfrac{1}{2}\).
Vậy có bốn số phức thỏa mãn bài toán là \({z_1} = \dfrac{{\sqrt 3 }}{2} + \dfrac{1}{2}i,\,\,{z_2} = \dfrac{{\sqrt 3 }}{2} - \dfrac{1}{2}i,\,\,{z_3} = - \dfrac{{\sqrt 3 }}{2} - \dfrac{1}{2}i,\,\,{z_4} = - \dfrac{{\sqrt 3 }}{2} + \dfrac{1}{2}i.\)
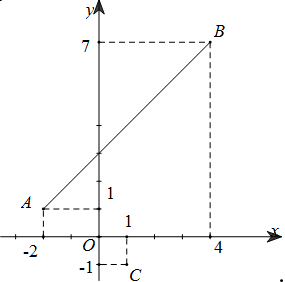
Xét số phức \(z\) thỏa mãn \(\left| {z + 2 - i} \right| + \left| {z - 4 - 7i} \right| = 6\sqrt 2 \). Gọi \(m,M\) lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của \(\left| {z - 1 + i} \right|\). Tính \(P = m + M\).
Gọi $z=x+yi\left( x,y\in R \right)$
Trên mặt phẳng tọa độ $Oxy$ gọi $P\left( {x;y} \right)$ là điểm biểu diễn của số phức $z$
Gọi $A\left( {-2;1} \right),B\left( {4;7} \right)$ thì
$\begin{array}{l}AB = 6\sqrt 2 = \left| {z + 2 - i} \right| + \left| {z - 4 - 7i} \right|\\ = \sqrt {{{\left( {x + 2} \right)}^2} + {{\left( {y - 1} \right)}^2}} + \sqrt {{{\left( {x - 4} \right)}^2} + {{\left( {y - 7} \right)}^2}} = PA + PB\end{array}$
Suy ra tập hợp các điểm $P$ thỏa mãn chính là đoạn thẳng AB
Có $\left| {z - 1 + i} \right| = \sqrt {{{\left( {x - 1} \right)}^2} + {{\left( {y + 1} \right)}^2}} = PC$ với $C\left( {1;-1} \right)$
Do đó \(P{C_{\min }}\) khi \(P\) là hình chiếu của \(C\) lên \(AB\) và \(P{C_{\max }}\) khi \(P \equiv B\)
Suy ra $M = CB = \sqrt {73} $.
Ta có: \(AB:\dfrac{{x + 2}}{{4 + 2}} = \dfrac{{y - 1}}{{7 - 1}} \Leftrightarrow x - y + 3 = 0\)\( \Rightarrow m=d\left( {C,AB} \right) = \dfrac{{\left| {1 - \left( { - 1} \right) + 3} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }} = \dfrac{5}{{\sqrt 2 }}\)
$\Rightarrow M + m = \dfrac{{5\sqrt 2 + 2\sqrt {73} }}{2}$
Cho số phức z thỏa mãn \(2iz + \overline z = 1 - i\). Phần thực của số phức \(z\) là:
Đặt \(z = a + bi\,\,\left( {a,b \in \mathbb{R}} \right)\)\( \Rightarrow \overline z = a - bi\).
Khi đó ta có:
\(\begin{array}{l}\,\,\,\,\,\,2iz + \overline z = 1 - i\\ \Leftrightarrow 2i\left( {a + bi} \right) + a - bi = 1 - i\\ \Leftrightarrow 2ai - 2b + a - bi = 1 - i\\ \Leftrightarrow \left( {a - 2b} \right) + \left( {2a - b} \right)i = 1 - i\\ \Rightarrow \left\{ \begin{array}{l}a - 2b = 1\\2a - b = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 1\\b = - 1\end{array} \right.\end{array}\)
\( \Rightarrow z = - 1 - i\).
Vậy phần thực số phức \(z\) là \( - 1\).
Cho số phức \(z = - \dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}i\). Số phức \(1 + z + {z^2}\) bằng:
Sử dụng MTCT ta có:
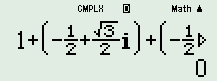
Biết \(1 + i\) là nghiệm của phương trình \(zi + azi + bz + a = 0\,\,\,\left( {a,b \in \mathbb{R}} \right)\) ẩn z trên tập số phức. Tìm \({b^2} - {a^3}.\)
Vì \(z = 1 + i\) là 1 nghiệm của phương trình \(zi + azi + bz + a = 0\,\,\,\left( {a,b \in \mathbb{R}} \right)\) nên ta có:
\(\begin{array}{l}\,\,\,\,\,\,\left( {1 + i} \right)i + a.\left( {i + 1} \right)i + b\left( {i + 1} \right) + a = 0\\ \Leftrightarrow - 1 + i + a\left( { - 1 + i} \right) + b + bi + a = 0\\ \Leftrightarrow b - 1 + \left( {1 + a + b} \right)i = 0\\ \Leftrightarrow \left\{ \begin{array}{l}b - 1 = 0\\1 + a + b = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}b = 1\\a = - 2\end{array} \right.\end{array}\)
Vậy \({b^2} - {a^3} = {1^2} - {\left( { - 2} \right)^3} = 9.\)
Có bao nhiêu số phức thỏa mãn \({z^2} + 2\left( {\overline z } \right) = 0\)?
Đặt \(z = a + bi \Rightarrow \overline z = a - bi.\)
Khi đó ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,{z^2} + 2\overline z = 0\\ \Leftrightarrow {\left( {a + bi} \right)^2} + 2\left( {a - bi} \right) = 0\\ \Leftrightarrow {a^2} + 2abi + {b^2}{i^2} + 2a - 2bi = 0\\ \Leftrightarrow {a^2} - {b^2} + 2a + \left( {2ab - 2b} \right)i = 0\\ \Leftrightarrow \left\{ \begin{array}{l}{a^2} - {b^2} + 2a = 0\\2ab - 2b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{a^2} - {b^2} + 2a = 0\\2b\left( {a - 1} \right) = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{a^2} - {b^2} + 2a = 0\\\left[ \begin{array}{l}b = 0\\a = 1\end{array} \right.\end{array} \right. \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}a = 1\\-{b^2} + 3 = 0\end{array} \right.\\\left\{ \begin{array}{l}b = 0\\{a^2} + 2a = 0\end{array} \right.\end{array} \right. \end{array}\)
$\begin{array}{l}
\Leftrightarrow \left[ \begin{array}{l}
\left\{ \begin{array}{l}
a = 1\\
b = \pm \sqrt 3
\end{array} \right.\\
\left\{ \begin{array}{l}
b = 0\\
\left[ \begin{array}{l}
a = 0\\
a = - 2
\end{array} \right.
\end{array} \right.
\end{array} \right.\\
\Rightarrow {z_1} = 1 + \sqrt 3 i,{z_2} = 1 - \sqrt 3 i\\
{z_3} = 0,{z_4} = - 2
\end{array}$
Vậy có 4 số phức thỏa mãn yêu cầu bài toán.
Biết rằng \(z = {m^2} - 3m + 3 + \left( {m - 2} \right)i\) \(\left( {m \in \mathbb{R}} \right)\) là một số thực. Giá trị của biểu thức \(1 + z + {z^2} + {z^3} + ... + {z^{2019}}\) bằng
Vì \(z = {m^2} - 3m + 3 + \left( {m - 2} \right)i\) là số thực nên \(m - 2 = 0 \Leftrightarrow m = 2.\)
Suy ra \(z = {m^2} - 3m + 3 = 1.\)
Vậy \(1 + z + {z^2} + ... + {z^{2019}} = 1 + 1 + 1 + ... + 1 = 2020\) (có 2020 số 1).
Với số phức \(z\) tùy ý, cho mệnh đề \(\left| { - z} \right| = \left| z \right|;\)\(\left| {\overline z } \right| = \left| z \right|;\)\(\left| {z + \overline z } \right| = 0;\)\(\left| z \right| > 0.\) Số mệnh đề đúng là:
+) Đặt \(z = a + bi \Rightarrow - z = - a - bi.\)
Ta có: \(\left| z \right| = \sqrt {{a^2} + {b^2}} ,\,\,\left| { - z} \right| = \sqrt {{{\left( { - a} \right)}^2} + {{\left( { - b} \right)}^2}} \) \( \Rightarrow \left| z \right| = \left| { - z} \right|\) là mệnh đề đúng.
+) Đặt \(z = a + bi \Rightarrow \overline z = a - bi.\)
Ta có: \(\left| z \right| = \sqrt {{a^2} + {b^2}} ,\,\,\left| {\overline z } \right| = \sqrt {{a^2} + {{\left( { - b} \right)}^2}} \) \( \Rightarrow \left| z \right| = \left| {\overline z } \right|\) là mệnh đề đúng.
+) Đặt \(z = a + bi \Rightarrow \overline z = a - bi \Rightarrow z + \overline z = 2a\)
\( \Rightarrow \left| {z + \overline z } \right| = \left| {2a} \right|\)\( \Rightarrow \left| {z + \overline z } \right| = 0\) là mệnh đề sai.
+) Đặt \(z = a + bi \Rightarrow \left| z \right| = \sqrt {{a^2} + {b^2}} \ge 0\)\( \Rightarrow \left| z \right| > 0\) là mệnh đề sai.
Vậy có 2 mệnh đề đúng.
Số phức liên hợp của số phức \(z = \dfrac{1}{{1 + i}}\) là:
Ta có \(z = \dfrac{1}{{1 + i}} = \dfrac{{1 - i}}{{\left( {1 + i} \right)\left( {1 - i} \right)}} \)\(= \dfrac{{1 - i}}{{1 - {i^2}}} = \dfrac{{1 - i}}{{1 + 1}} = \dfrac{{1 - i}}{2}= \dfrac{1}{2} - \dfrac{1}{2}i \)
\(\Rightarrow \overline z = \dfrac{1}{2} + \dfrac{1}{2}i\).
Biết số phức \(z\) thỏa mãn \({z^{ - 1}} = 1 + 2i,\) phần ảo của \(z\) bằng:
Ta có: \({z^{ - 1}} = 1 + 2i\) \( \Rightarrow \dfrac{1}{z} = 1 + 2i\) \( \Leftrightarrow z = \dfrac{1}{{1 + 2i}} = \dfrac{{1 - 2i}}{{1 - {{\left( {2i} \right)}^2}}}\)\( = \dfrac{{1 - 2i}}{{1 + 4}} = \dfrac{1}{5} - \dfrac{2}{5}i\)
\( \Rightarrow \) Số phức \(z\) có phần ảo là \( - \dfrac{2}{5}.\)
Số phức nghịch đảo của \(z = 3 + 4i\) là:
Số phức nghịch đảo của số phức \(z = 3 + 4i\) là: \(\dfrac{1}{{3 + 4i}} = \dfrac{{3 - 4i}}{{{3^2} - {{\left( {4i} \right)}^2}}}\) \( = \dfrac{{3 - 4i}}{{9 + 16}} = \dfrac{3}{{25}} - \dfrac{4}{{25}}i.\)
Trên \(\mathbb{C}\) phương trình \(\dfrac{2}{{z - 1}} = 1 + i\) có nghiệm là:
\(\dfrac{2}{{z - 1}} = 1 + i \Leftrightarrow z - 1 = \dfrac{2}{{1 + i}} \Leftrightarrow z - 1 = 1 - i \Leftrightarrow z = 2 - i\)

