Với giá trị nào của \(m\) thì hai đường thẳng \(\left( {{\Delta _1}} \right):3x + 4y - 1 = 0\) và \(\left( {{\Delta _2}} \right):\left( {2m - 1} \right)x + {m^2}y + 1 = 0\) trùng nhau.
Ta có: \({\Delta _1} \equiv {\Delta _1} \Leftrightarrow \dfrac{{2m - 1}}{3} = \dfrac{{{m^2}}}{4} = \dfrac{1}{{ - 1}} \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{2m - 1}}{3} = - 1\\\dfrac{{{m^2}}}{4} = - 1\left( {VN} \right)\end{array} \right.\)
Vậy không có giá trị nào của \(m\) thỏa mãn.
Trong mặt phẳng với hệ toạ độ $Oxy,$ cho hình vuông $ABCD$ biết $M\left( {2;1} \right);N\left( {4;-2} \right);P\left( {2;0} \right);Q\left( {1;2} \right)$ lần lượt thuộc cạnh $AB,BC,CD,AD.$ Hãy lập phương trình cạnh $AB$ của hình vuông.
Giả sử đường thẳng $AB$ qua $M$ và có VTPT là $\vec n = \left( {a;b} \right)\,\,\,\,\left( {{a^2} + {b^2} \ne 0} \right)$
=> VTPT của $BC$ là: ${\vec n_1} = \left( { - b;a} \right)$.
Phương trình AB có dạng: $a\left( {x-2} \right) + b\left( {y-1} \right) = 0$ $ \Leftrightarrow ax + by-2a-b = 0$
BC có dạng: $-b\left( {x-4} \right) + a\left( {y + 2} \right) = 0\;$ $ \Leftrightarrow -bx + ay + 4b + 2a = 0$
Do $ABCD$ là hình vuông nên $d\left( {P,AB} \right) = d\left( {Q,BC} \right)$
$ \Leftrightarrow \dfrac{{\left| { - b} \right|}}{{\sqrt {{a^2} + {b^2}} }} = \dfrac{{\left| {3b + 4a} \right|}}{{\sqrt {{a^2} + {b^2}} }} \Leftrightarrow \left[ \begin{array}{l}b = - 2a\\b = - a\end{array} \right.$
TH1: \(b = - 2a\)
Chọn \(a = 1 \Rightarrow b = - 2\) ta được \(AB:x - 2y - 2.1 - \left( { - 2} \right) = 0\) hay \(x - 2y = 0\)
\(BC: - \left( { - 2} \right)x + y + 4.\left( { - 2} \right) + 2.1 = 0\) hay \(2x + y - 6 = 0\)
CD đi qua P(2;0) và song song AB nên nhận \(\overrightarrow {{n_{AB}}} = \left( {1; - 2} \right)\) làm VTPT
Do đó CD: 1(x-2) – 2(y-0) = 0 hay x-2y-2=0
AD đi qua Q(1;2) và song song BC nên nhận \(\overrightarrow {{n_{BC}}} = \left( {2;1} \right)\) làm VTPT
Do đó AD: 2(x-1) + 1(y-2) = 0 hay 2x+y-4=0
TH2: \(b = - a\)
Chọn \(a = 1 \Rightarrow b = - 1\) ta được \(AB:x - y - 2.1 - \left( { - 1} \right) = 0\) hay \(x - y - 1 = 0\)
\(BC: - \left( { - 1} \right)x + y + 4.\left( { - 1} \right) + 2.1 = 0\) hay \(x + y - 2 = 0\)
CD đi qua P(2;0) và song song AB nên nhận \(\overrightarrow {{n_{AB}}} = \left( {1; - 1} \right)\) làm VTPT
Do đó CD: 1(x-2) – 1(y-0) = 0 hay x-y-2=0
AD đi qua Q(1;2) và song song BC nên nhận \(\overrightarrow {{n_{BC}}} = \left( {1;1} \right)\) làm VTPT
Do đó AD: 1(x-1) + 1(y-2) = 0 hay x+y-3=0.
Trong mặt phẳng với hệ tọa độ \(Oxy\), cho đường thẳng \(\Delta :3x + y + 6 = 0\) và điểm \(M\left( {1;3} \right).\) Viết phương trình đường thẳng \(d\) biết \(d\) đi qua \(M\) và song song đường thẳng \(\Delta \).
Ta có: \(\Delta \) nhận \(\overrightarrow n = \left( {3;1} \right)\) là một VTPT.
Vì \(d//\Delta \Rightarrow \overrightarrow n \) cũng là VTPT của d.
\( \Rightarrow \) Phương trình d: \(3\left( {x - 1} \right) + 1\left( {y - 3} \right) = 0 \Leftrightarrow 3x + y - 6 = 0.\)
Trong mặt phẳng với hệ tọa độ $Oxy,$ cho $\Delta ABC$ cân có đáy là $BC.$ Đỉnh $A$ có tọa độ là các số dương, hai điểm $B$ và $C$ nằm trên trục $Ox,$ phương trình cạnh $AB:$ $y = 3\sqrt 7 (x - 1)$. Biết chu vi của $\Delta ABC$ bằng $18,$ tìm tọa độ các đỉnh $A,B,C.$
$B = AB \cap Ox \Rightarrow B(1;0)$, $A \in AB \Rightarrow A\left( {a;3\sqrt 7 (a - 1)} \right) \Rightarrow a > 1$ (do ${x_A} > 0,{y_A} > 0$).
Gọi $AH$ là đường cao \(\Delta ABC\), do \(\Delta ABC\) cân tại $A$ nên $AH$ cũng là đường trung tuyến, khi đó $H$ là trung điểm của $BC$
$ \Rightarrow H(a;0) \Rightarrow C(2a - 1;0) \Rightarrow BC = 2(a - 1),AB = AC = 8(a - 1)$
Chu vi tam giác \(ABC\) bằng \(18\) $ \Leftrightarrow a = 2 \Rightarrow C(3;0),A\left( {2;3\sqrt 7 } \right)$
Trong mặt phẳng với hệ toạ độ $Oxy,$ cho \(\Delta ABC\) có đỉnh $A\left( {1;2} \right),$ phương trình đường trung tuyến \(BM:2x + y + 1 = 0\) và phân giác trong \(CD:x + y - 1 = 0\). Viết phương trình đường thẳng $BC.$
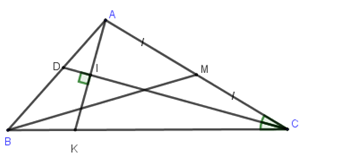
Điểm \(C \in CD:x + y - 1 = 0 \Rightarrow C\left( {t;1 - t} \right)\).
Suy ra trung điểm $M$ của $AC$ là \(M\left( {\dfrac{{t + 1}}{2};\dfrac{{3 - t}}{2}} \right)\).
$M$ thuộc $BM$ nên \((t + 1) + \dfrac{{3 - t}}{2} + 1 = 0 \Rightarrow t = - 7 \Rightarrow C\left( { - 7;8} \right)\)
Từ $A\left( {1;2} \right),$ kẻ \(AI \bot CD\left( {I \in CD} \right)\) cắt \(BC\) tại \(K\)
Suy ra \(AK:\left( {x - 1} \right) - \left( {y - 2} \right) = 0 \Leftrightarrow x - y + 1 = 0\)
Tọa độ điểm $I$ thỏa hệ: \(\left\{ \begin{array}{l}x + y - 1 = 0\\x - y + 1 = 0\end{array} \right. \Rightarrow I\left( {0;1} \right)\)
Tam giác $ACK$ cân tại $C$ nên $I$ là trung điểm của $AK \Rightarrow K\left( { - 1;0} \right)$
Đường thẳng $BC$ đi qua $C,K$ nên có phương trình:
\(\dfrac{{x + 1}}{{ - 7 + 1}} = \dfrac{y}{8} \Leftrightarrow 4x + 3y + 4 = 0\)
Trong mặt phẳng với hệ toạ độ $Oxy,$ cho tam giác $ABC$ có phương trình đường phân giác trong góc $A$ là ${d_1}:x + y + 2 = 0,$ phương trình đường cao vẽ từ $B$ là ${d_2}:2x-y + 1 = 0,$ cạnh $AB$ đi qua $M\left( {1;-1} \right).$ Tìm phương trình cạnh $AC.$
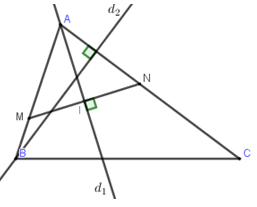
Gọi $N$ là điểm đối xứng của $M$ qua \({d_1} \Rightarrow N \in AC\)
\(\overrightarrow {MN} = ({x_N} - 1,\,\,{y_N} + 1)\)
Ta có: \(\overrightarrow {MN} \) cùng phương \({\overrightarrow n _{{d_1}}} = (1;\,\,1)\)
\( \Leftrightarrow \,\,1({x_N} - 1) - 1({y_N} + 1) = 0\)\( \Leftrightarrow {x_N} - {y_N} = 2\,\,\,(1)\)
Tọa độ trung điểm $I$ của \(MN:\)\({x_I} = \dfrac{1}{2}\left( {1 + {x_N}} \right),{y_I} = \dfrac{1}{2}\left( { - 1 + {y_N}} \right)\)
\(I \in \left( {{d_1}} \right) \Leftrightarrow \dfrac{1}{2}\left( {1 + {x_N}} \right) + \dfrac{1}{2}\left( { - 1 + {y_N}} \right) + 2 = 0\)\( \Leftrightarrow {x_N} + {y_N} + 4 = 0\,\,\,\,(2)\)
Giải hệ $\left( 1 \right)$ và $\left( 2 \right)$ ta được $N\left( {-1;-3} \right)$
Phương trình cạnh $AC$ vuông góc với \({d_2}\) có dạng: $x + 2y + C = 0.$
\(N \in AC\)\( \Leftrightarrow - 1 + 2.( - 3) + C = 0\)\( \Leftrightarrow C = 7\)
Vậy, phương trình cạnh $AC:$ $x + 2y + 7 = 0.$
Trong mặt phẳng với hệ trục tọa độ Oxy, cho đường thẳng \(\left( d \right):3x - 4y - 12 = 0\). Phương trình đường thẳng \(\left( \Delta \right)\) đi qua \(M\left( {2; - 1} \right)\) và tạo với \(\left( d \right)\) một góc \({45^o}\) có dạng \(ax + by + 5 = 0\), trong đó a,b cùng dấu. Khẳng định nào sau đây đúng?
Đường thẳng \(\left( d \right)\) có VTPT \(\overrightarrow {{n_1}} = \left( {3; - 4} \right)\)
Đường thẳng \(\left( \Delta \right)\) có VTPT \(\overrightarrow {{n_2}} = \left( {a;b} \right)\)
\(\begin{array}{l} \Rightarrow \cos \left( {d;\Delta } \right) = \cos \left( {\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} } \right) = \dfrac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \dfrac{{\left| {3a - 4b} \right|}}{{5\sqrt {{a^2} + {b^2}} }}\\ \Leftrightarrow \cos {45^o} = \dfrac{{\left| {3a - 4b} \right|}}{{5\sqrt {{a^2} + {b^2}} }} \Leftrightarrow \dfrac{{\left| {3a - 4b} \right|}}{{5\sqrt {{a^2} + {b^2}} }} = \dfrac{{\sqrt 2 }}{2}\\ \Leftrightarrow \sqrt 2 \left| {3a - 4b} \right| = 5\sqrt {{a^2} + {b^2}} \Leftrightarrow 2{\left( {3a - 4b} \right)^2} = 25\left( {{a^2} + {b^2}} \right)\\ \Leftrightarrow 7{a^2} + 48ab - 7{b^2} = 0\,\,\,\,\,\,\left( 1 \right)\end{array}\)
Mặt khác \(M\left( {2; - 1} \right) \in \Delta \Rightarrow 2a - b + 5 = 0 \Leftrightarrow b = 2a + 5\) thế vào (1)
\(\begin{array}{l} \Rightarrow 7{a^2} + 48a\left( {2a + 5} \right) - 7{\left( {2a + 5} \right)^2} = 0 \Leftrightarrow 75{a^2} + 100a - 175 = 0 \Leftrightarrow \left[ \begin{array}{l}a = 1 \Rightarrow b = 7\,\,\,\,\,(tm)\\a = - \dfrac{7}{3} \Rightarrow b = \dfrac{1}{3}\,\,\,(ktm)\end{array} \right.\\ \Rightarrow a + b = 8.\end{array}\)Trong mặt phẳng với hệ tọa độ \(Oxy\), cho đường thẳng đi qua hai điểm \(A\left( {1;2} \right)\), \(B\left( {4;6} \right)\), tìm tọa độ điểm \(M\) trên trục \(Oy\) sao cho diện tích \(\Delta MAB\) bằng 1.
Gọi \(M\left( {0;m} \right) \in Oy;\,\,AB = \sqrt {{{\left( {4 - 1} \right)}^2} + {{\left( {6 - 2} \right)}^2}} = 5.\)
Có \({S_{\Delta MAB}} = \dfrac{1}{2}d\left( {M,AB} \right).AB\) \( \Leftrightarrow 1 = \dfrac{1}{2}.d\left( {M,AB} \right).5 \Leftrightarrow d\left( {M,AB} \right) = \dfrac{2}{5}\)
\(\overrightarrow {AB} = \left( {3;4} \right) \Rightarrow \overrightarrow n = \left( {4; - 3} \right)\) là 1 VTPT của AB.
\( \Rightarrow \) Phương trình AB: \(4\left( {x - 1} \right) - 3\left( {y - 2} \right) = 0 \Leftrightarrow 4x - 3y + 2 = 0\)
\( \Rightarrow d\left( {M,AB} \right) = \dfrac{{\left| { - 3m + 2} \right|}}{{\sqrt {{4^2} + {3^2}} }}\)\( \Leftrightarrow \dfrac{2}{5} = \dfrac{{\left| { - 3m + 2} \right|}}{5} \Leftrightarrow \left| { - 3m + 2} \right| = 2\)
\( \Leftrightarrow \left[ \begin{array}{l} - 3m + 2 = 2\\ - 3m + 2 = - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0 \Rightarrow M\left( {0;0} \right)\\m = \dfrac{4}{3} \Rightarrow M\left( {0;\dfrac{4}{3}} \right)\end{array} \right.\)

