I. Giao của mặt phẳng với mặt nón tròn xoay
Giao của một mặt nón tròn xoay với một mặt phẳng không đi qua đỉnh là một đường tròn hoặc đường conic.
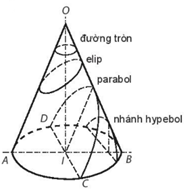
II. Xác định đường conic theo tâm sai, tiêu điểm và đường chuẩn
Trong mặt phẳng cho điểm F cố định và một đường thẳng A cố định không đi qua F.
Tập hợp các điểm M sao cho tỉ số \(\dfrac{{MF}}{{d\left( {M,\Delta } \right)}}\) bằng một số dương \(e\) cho trước được gọi là đường conic.
Điểm F gọi là tiêu điểm, đường thẳng \(\Delta \) gọi là đường chuẩn tương ứng với F và \(e\) gọi là tâm sai của đường conic.
Ta có:
- Nếu tâm sai \(e < 1\) thì đường conic nhận được là đường elip.
- Nếu tâm sai \(e = 1\) thì đường conic nhận được là đường parabol.
- Nếu tâm sai \(e > 1\) thì đường conic nhận được là đường hypebol.
