I. Sơ đồ tư duy Định lý côsin và định lý sin
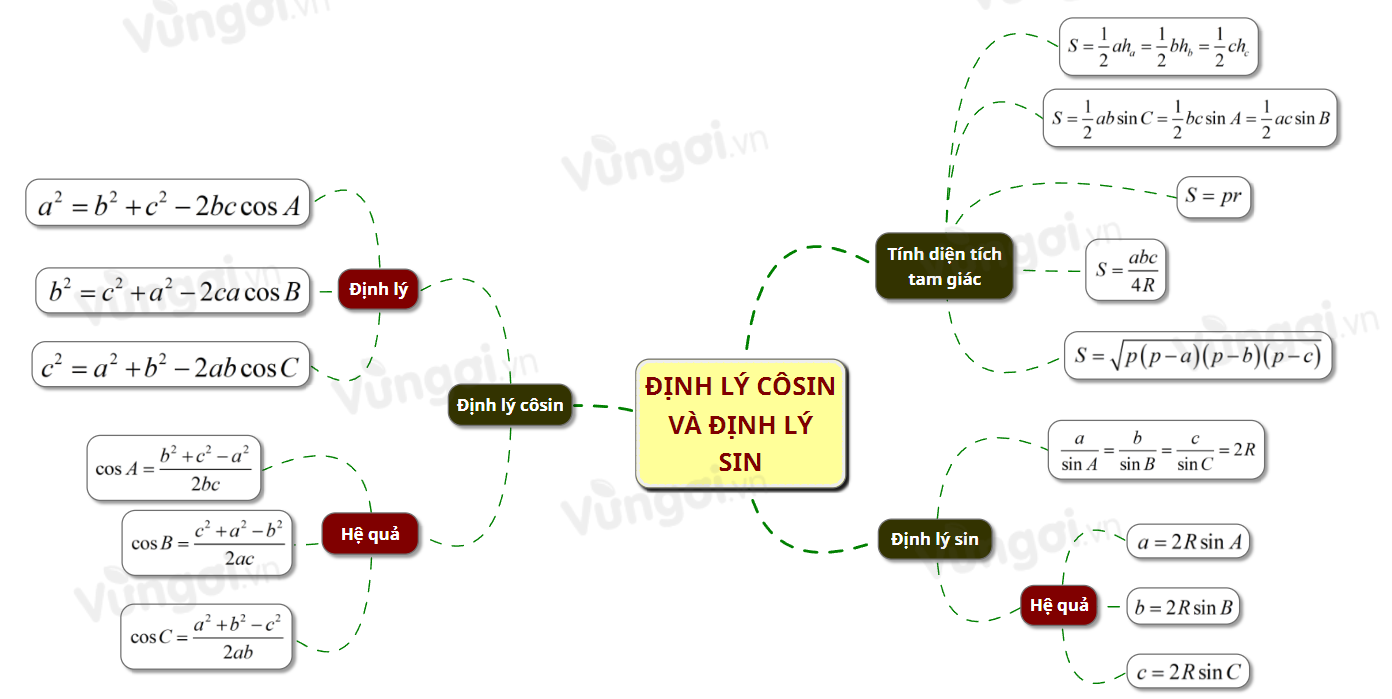
II. Định lí côsin
Cho tam giác $A B C$ có \(BC = a,CA = b,AB = c\). Khi đó:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc\cos A\\{b^2} = {c^2} + {a^2} - 2ca\cos B\\{c^2} = {a^2} + {b^2} - 2ab\cos C\end{array}\)
Hệ quả
\(\begin{array}{l}\cos A = \dfrac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\\\cos B = \dfrac{{{c^2} + {a^2} - {b^2}}}{{2ca}}\\\cos C = \dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\end{array}\)
III. Định lí sin
Cho tam giác \(ABC\;{\rm{ có }}\;BC = a,CA = b,AB = c\) và bán kính đường tròn ngoại tiếp là $R$. Khi đó:
\(\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = 2R\)
Hệ quả:
\(a = 2R\sin A\)
\(b = 2R\sin B\)
\(c = 2R\sin C\)
IV. Tính diện tích tam giác
Cho tam giác $ABC$. Ta kí hiệu:
- \({h_a},{h_b},{h_c}\) là độ dài các đường cao lần lượt ứng với các cạnh $BC, CA, AB$.
- $R$ là bán kính đường tròn ngoại tiếp tam giác.
- $r$ là bán kính đường tròn nội tiếp tam giác.
- $p$ là nửa chu vi tam giác.
- S là diện tích tam giác.
Ta có các công thức tính diện tích tam giác sau:
1) \(S = \dfrac{1}{2}a{h_a} = \dfrac{1}{2}b{h_b} = \dfrac{1}{2}c{h_c}\);
2) \(S = \dfrac{1}{2}ab\sin C = \dfrac{1}{2}bc\sin A = \dfrac{1}{2}ac\sin B\);
3) \(S = \dfrac{{abc}}{{4R}}\);
4) \(S = pr\);
5) \(S = \sqrt {p(p - a)(p - b)(p - c)} \) (công thức Heron).

