I. Sơ đồ tư duy Ôn tập cuối chương IV
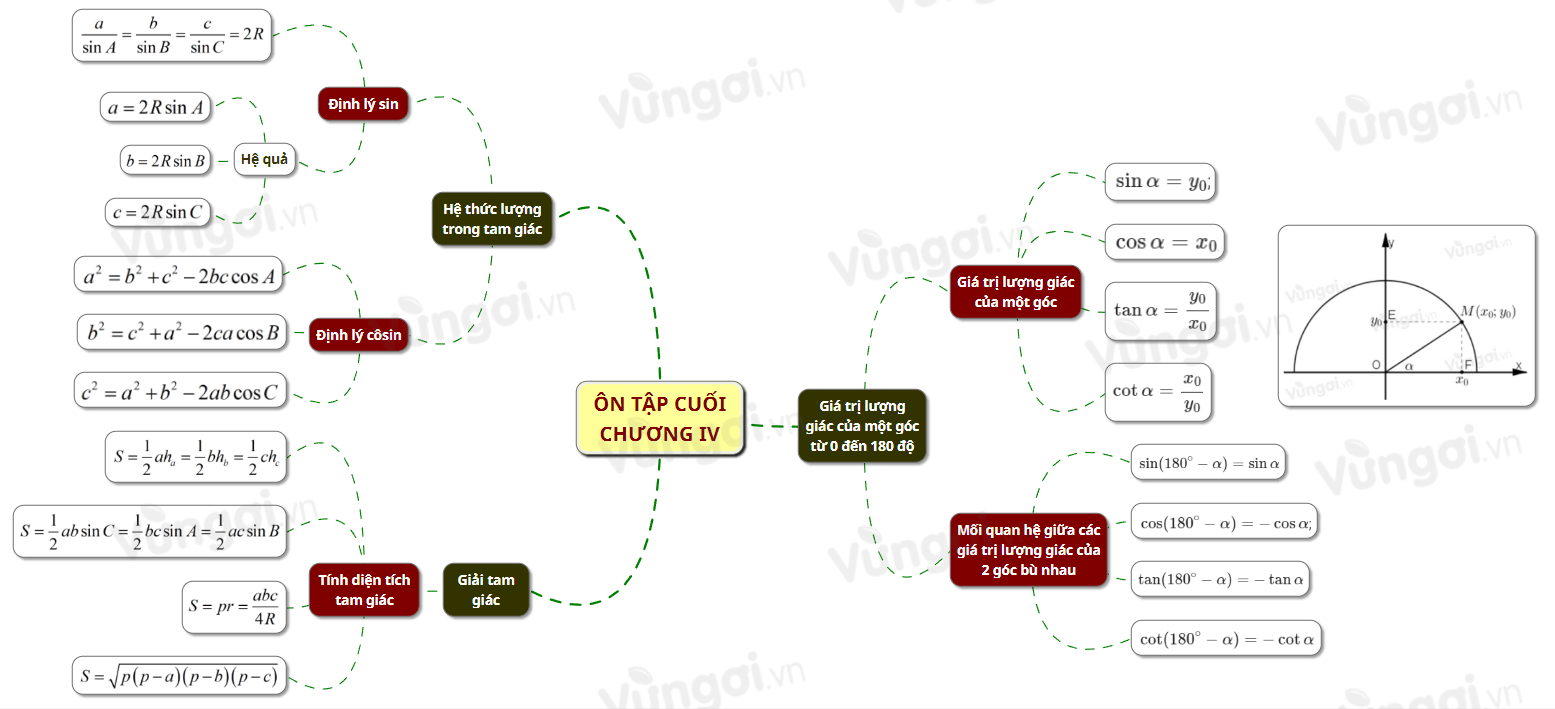
II. Giá trị lượng giác của một góc từ 0 đến 180
1. Giá trị lượng giác của một góc
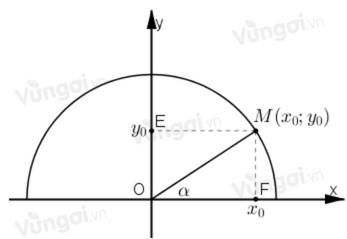
- sin của góc \(\alpha \), kí hiệu là \(\sin \alpha \), được xác định bởi: \(\sin \alpha = {y_0}\);
- côsin của góc \(\alpha \), kí hiệu là \(\cos \alpha \), được xác định bởi: \(\cos \alpha = {x_0}\);
- tang của góc \(\alpha \), kí hiệu là tan \(\alpha \), được xác định bởi: \(\tan \alpha = \dfrac{{{y_0}}}{{{x_0}}}\left( {{x_0} \ne 0} \right)\);
- côtang của góc \(\alpha \), kí hiệu là \(\cot \alpha \), được xác định bởi: \(\cot \alpha = \dfrac{{{x_0}}}{{{y_0}}}\left( {{y_0} \ne 0} \right)\).
Các số \(\sin \alpha ,\cos \alpha ,\tan \alpha ,\cot \alpha \) được gọi là các giá trị lượng giác của góc \(\alpha \).
Bảng giá trị lượng giác của một số góc đặc biệt:
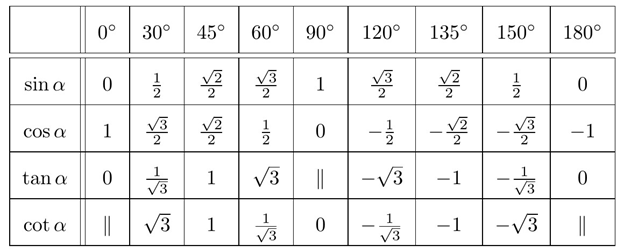
2. Mối quan hệ giữa các giá trị lượng giác của hai góc bù nhau
Đối với hai góc bù nhau, \(\alpha \) và \({180^\circ } - \alpha \), ta có:
- \(\sin \left( {{{180}^\circ } - \alpha } \right) = \sin \alpha \);
- \(\cos \left( {{{180}^\circ } - \alpha } \right) = - \cos \alpha \);
- \(\tan \left( {{{180}^\circ } - \alpha } \right) = - \tan \alpha \left( {\alpha \ne {{90}^\circ }} \right)\)
- \(\cot \left( {{{180}^\circ } - \alpha } \right) = - \cot \alpha \left( {{0^\circ } < \alpha < {{180}^\circ }} \right)\).
3. Sử dụng MTCT để tính giá trị lượng giác của một góc
- Để tính các giá trị lượng giác bằng MTCT, sau khi đưa máy về chế độ “độ” ta làm như sau:
- Tính góc khi biết một giá trị lượng giác của góc đó:
III. Định lí côsin và định lí sin trong tam giác
1. Định lí côsin
Cho tam giác $A B C$ có \(BC = a,CA = b,AB = c\). Khi đó:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc\cos A\\{b^2} = {c^2} + {a^2} - 2ca\cos B\\{c^2} = {a^2} + {b^2} - 2ab\cos C\end{array}\)
Hệ quả
\(\begin{array}{l}\cos A = \dfrac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\\\cos B = \dfrac{{{c^2} + {a^2} - {b^2}}}{{2ca}}\\\cos C = \dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\end{array}\)
2. Định lí sin
Cho tam giác \(ABC\) có \(BC = a,CA = b,AB = c\) và bán kính đường tròn ngoại tiếp là R. Khi đó:
\(\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = 2R\)
Hệ quả:
\(a = 2R\sin A\)
\(b = 2R\sin B\)
\(c = 2R\sin C\)
IV. Giải tam giác
1. Tính các cạnh và góc của tam giác dựa trên một số điều kiện cho trước
Như ta đã biết, một tam giác hoàn toàn xác định nếu biết một trong những dữ kiện sau:
- Biết độ dài hai cạnh và độ lớn góc xen giữa hai cạnh đó;
- Biết độ dài ba cạnh;
- Biết độ dài một cạnh và độ lớn hai góc kề với cạnh đó.
2. Tính diện tích tam giác
Cho tam giác $ABC$. Ta kí hiệu:
- \({h_a},{h_b},{h_c}\) là độ dài các đường cao lần lượt ứng với các cạnh $BC, CA, AB$.
- $R$ là bán kính đường tròn ngoại tiếp tam giác.
- $r$ là bán kính đường tròn nội tiếp tam giác.
- $p$ là nửa chu vi tam giác.
- S là diện tích tam giác.
Ta có các công thức tính diện tích tam giác sau:
1) \(S = \dfrac{1}{2}a{h_a} = \dfrac{1}{2}b{h_b} = \dfrac{1}{2}c{h_c}\);
2) \(S = \dfrac{1}{2}ab\sin C = \dfrac{1}{2}bc\sin A = \dfrac{1}{2}ac\sin B\);
3) \(S = \dfrac{{abc}}{{4R}}\);
4) \(S = pr\);
5) \(S = \sqrt {p(p - a)(p - b)(p - c)} \) (công thức Heron).
