I. Hoán vị
Tập hợp hữu hạn \(A\) có \(n\) phần tử \(\left( {n \ge 1} \right)\). Mỗi cách sắp thứ tự các phần tử của \(A\) được gọi là một hoán vị của \(n\) phần tử đó.
Số các hoán vị khác nhau của \(n\) phần tử là:
\(P = n\left( {n - 1} \right)\left( {n - 2} \right)...2.1 = n!\)
Chú ý: Kí hiệu \(n.\left( {n - 1} \right).\left( {n - 2} \right)...{\rm{ }}2.1\) là \(n!\) (đọc là \(n\) giai thừa hoặc giai thừa của \(n\)), ta có \({P_n} = n!\)
Chẳng hạn \({P_3} = 3! = 3.2.1 = 6.\)
Quy ước \(0! = 1.\)
Ví dụ: Có bao nhiêu cách xếp \(3\) bạn vào một bàn có \(3\) chỗ ngồi?
Giải:
Mỗi cách xếp cho ta một hoán vị khác nhau của \(3\) bạn. Vậy số cách xếp là \({P_3} = 3! = 6\).
II. Chỉnh hợp
Xét một tập hợp \(A\) gồm \(n\) phần tử \(\left( {n \ge 1} \right)\) và một số nguyên \(k\) với \(1 \le k \le n\). Mỗi cách lấy ra \(k\) phần tử của \(A\) và sắp xếp chúng theo một thứ tự nào đó được gọi là chỉnh hợp chập \(k\) của \(n\) phần tử của \(A\).
Số chỉnh hợp chập \(k\) của \(n\) phần tử là:
$A_n^k = \dfrac{{n!}}{{\left( {n - k} \right)!}} = n\left( {n - 1} \right)\left( {n - 2} \right)...\left( {n - k + 1} \right)$
Ví dụ: Có bao nhiêu số nguyên dương gồm \(3\) chữ số đôi một khác nhau và khác \(0\)?
Giải:
Mỗi số cần tìm có dạng \(\overline {abc} \left( {a,b,c \in \left\{ {1;2;3;...;9} \right\},a \ne b \ne c} \right)\).
Mỗi số dạng trên là một chỉnh hợp chập \(3\) của \(9\). Do đó số các số cần tìm là: \(A_9^3 = \dfrac{{9!}}{{\left( {9 - 3} \right)!}} = 9.8.7 = 504\) số.
Chú ý:
- Hoán vị sắp xếp tất cả các phần tử của tập hợp, còn chỉnh hợp chọn ra một số phần tử và sắp xếp chúng.
- Mỗi hoán vị của \(n\) phần tử cũng chính là một chỉnh hợp chập \(n\) của \(n\) phần tử đó. Vì vậy \({P_n} = A_n^n\)
III. Định nghĩa tổ hợp
Cho tập hợp A gồm n phần tử và một số nguyên k với \(1 < k \le n\).
Mỗi tập con gồm k phần tử được lấy ra từ n phần tử của A được gọi là một tổ hợp chập k của n phần tử đó.
Ví dụ: Bạn Quân có 4 chiếc áo sơ mi khác màu là áo vàng, áo xanh, áo trắng và áo nâu.
Bạn muốn chọn 2 chiếc áo để mặc khi đi du lịch. Viết các tổ hợp chập 2 của 4 chiếc áo.
Giải
Các tổ hợp chập 2 của 4 chiếc áo là:
{áo vàng; áo xanh}, {áo vàng; áo trắng}, {áo vàng; áo nâu},
{áo xanh; áo trắng}, {áo xanh; áo nâu}, {áo trắng; áo nâu}.
IV. Số các tổ hợp
Số các tổ hợp chập \(k\) của \(n\) phần tử \(\left( {1 \le k \le n} \right)\) bằng
\(C_n^k = \frac{{n!}}{{k!\left( {n - k} \right)!}}\)
Chú ý:
+ Quy ước \(C_n^0 = 1\)
+ \(C_n^k = \dfrac{{A_n^k}}{{k!}}\)
- Chỉnh hợp và tổ hợp có điểm giống nhau là đều chọn một số phần tử trong một tập hợp, nhưng khác nhau ở chỗ, chỉnh hợp là chọn có xếp thứ tự, còn tổ hợp là chọn không xếp thứ tự.
Ví dụ: Có 7 bạn học sinh muốn chơi cờ cá ngựa, nhưng mỗi ván chỉ có 4 người chơi. Hỏi có bao nhiêu cách chọn 4 bạn chơi cờ cá ngựa?
Giải
Mỗi cách chọn 4 bạn trong 7 bạn học sinh là một tổ hợp chập 4 của 7.
Vậy số cách chọn 4 bạn chơi cờ cá ngựa là: \(C_7^4 = \dfrac{{7!}}{{4!3!}} = 35\)
V. Tính chất tổ hợp chập k của n phần tử Ta có hai đẳng thức sau:
Ta có hai đẳng thức sau:
+\(C_n^k = C_n^{n - k}\left( {0 \le k \le n} \right)\)
+\(C_{n - 1}^{k - 1} + C_{n - 1}^k = C_n^k\left( {1 \le k < n} \right)\)
Ví dụ:
a) \(C_9^4 = C_9^5\)
b) \(C_8^3 + C_8^4 = C_9^4\)
VI. Tính số các hoán vị, chỉnh hợp, tổ hợp bằng máy tính cầm tay
1.Hoán vị
Để tính \({P_8} = 8!\), ta ấn liên tiếp các phím:

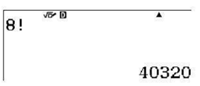
Ta được kết quả là 40 320
2.Chỉnh hợp
Để tính \(A_{12}^5\), ta ấn liên tiếp các phím:


Ta nhận được kết quả là 95 040.
3.Tổ hợp
Để tính \(C_{20}^{11}\), ta ấn liên tiếp các phím:
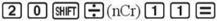

Ta nhận được kết quả là 167 960.

