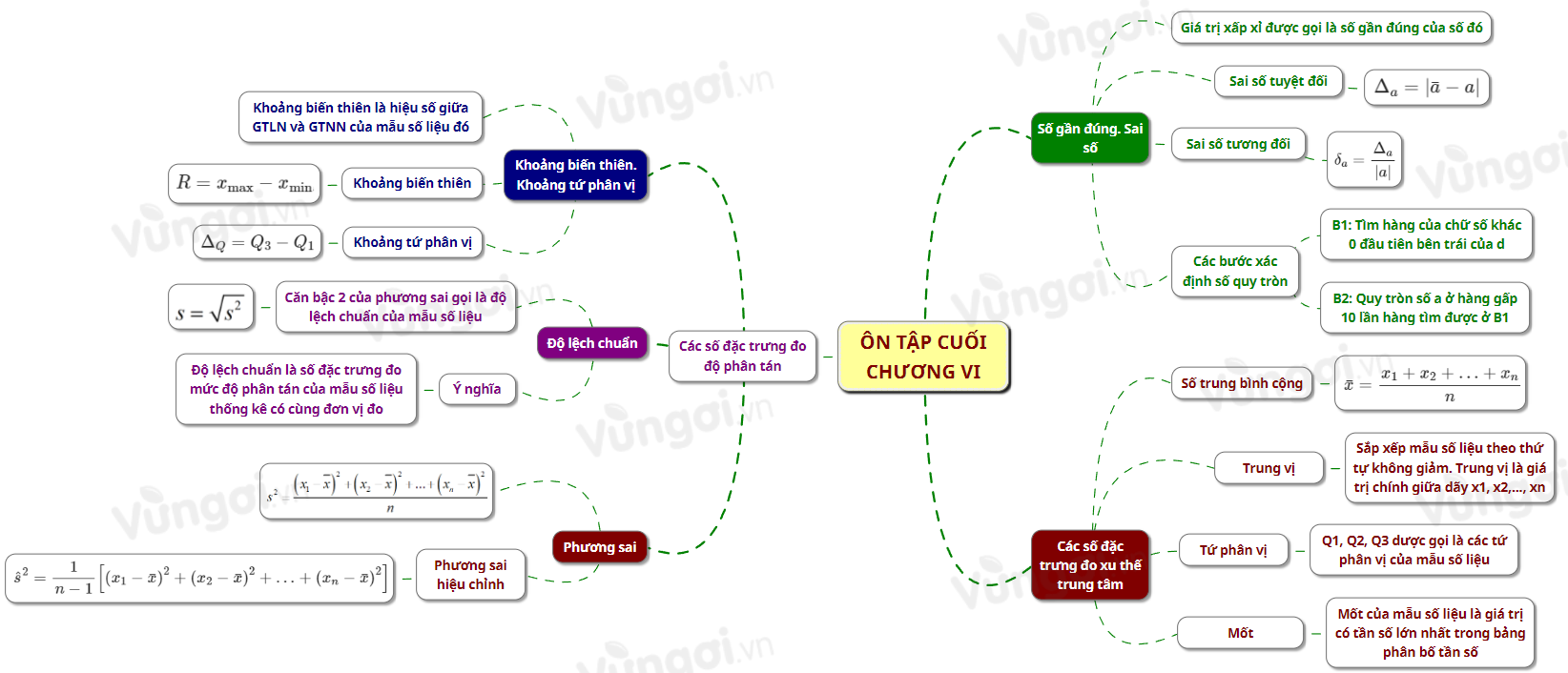
I. Sơ đồ tư duy ôn tập cuối chương VI
II. Số gần đúng. Sai số
1. Số gần đúng
- Trong nhiều trường hợp, ta không biết hoặc khó biết số đúng (kí hiệu là \(\bar a\) ) mà chỉ tìm được giá trị khác xấp xỉ nó. Giá trị này được gọi là số gần đúng, kí hiệu là \(a\).
- Trong đo đạc, tính toán ta thường chỉ nhận được các số gần đúng.
2. Sai số của số gần đúng
a. Sai số tuyệt đối
Nếu a là số gần đúng của số đúng \(\bar a\) thì \({\Delta _a} = \left| {\bar a - a} \right|\) được gọi là sai số tuyệt đối của số gần đúng a.
Chú ý
- Trên thực tế, nhiều khi ta không biết \(\bar a\) nên cũng không biết \({\Delta _a}\). Tuy nhiên, ta có thể đánh giá được \({\Delta _a}\) không vượt quá một số dương \(d\) nào đó.
- Nếu \({\Delta _a} \le d\) thì \(a - d \le \bar a \le a + d\), khi đó ta viết \(\bar a = a \pm d\) và hiểu là số đúng \(\bar a\) nằm trong đoạn \([a - d;a + d]\). Do \(d\) càng nhỏ thì a càng gần \(\bar a\) nên \(d\) được gọi là độ chính xác của số gần đúng.
- Trong các phép đo, độ chính xác \(d\) của số gần đúng bằng một nửa đơn vị của thước đo.
b. Sai số tương đối
Sai số tương đối của số gần đúng a là tỉ số giữa sai số tuyệt đối và \(\left| a \right|\), kí hiệu \({\delta _a} = \dfrac{{{\Delta _a}}}{{\left| a \right|}}\).
\({\delta _a}\) càng nhỏ thì độ chính xác của phép đo đạc hoặc tính toán càng lớn.
Ta thường viết \({\delta _a}\) dưới dạng phần trăm.
3. Số quy tròn. Quy tròn số gần đúng
Khi quy tròn một số nguyên hoặc một số thập phân đến một hàng nào đó thì số nhận được gọi là số quy tròn của số ban đầu.
- Các bước xác định số quy tròn của số gần đúng \(a\) với độ chính xác \(d\) cho trước:
Bước 1: Tìm hàng của chữ số khác 0 đầu tiên bên trái của \(d\).
Bước 2: Quy tròn số \(a\) ở hàng gấp 10 lần hàng tìm được ở Bước 1 .
- Để tìm số gần đúng \(a\) của số đúng \(\bar a\) với độ chính xác \(d\), ta thực hiện các bước sau:
Bước 1: Tìm hàng của chữ số khác 0 đầu tiên bên trái của \(d\).
Bước 2: Quy tròn \(\bar a\) đến hàng tìm được ở trên.
III. Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ
Dựa vào các thông tin đã biết và sử dụng mối liên hệ toán học giữa các số liệu, ta có thể phát hiện ra được số liệu không chính xác trong một số trường hợp.
Ví dụ:
Một đội 20 thợ thủ công được chia đều vào 5 tổ. Trong một ngày, mỗi người thợ làm được 4 hoặc 5 sản phẩm. Cuối ngày, đội trưởng thống kê lại số sản phẩm mà mỗi tổ làm được ở bảng sau:

Đội trưởng đã thống kê đúng chưa? Tại sao?
Giải
Mỗi tổ có \(20:5 = 4\) người. Trong một ngày, mỗi người thợ làm được 4 hoặc 5 sản phẩm nên mỗi tổ làm được từ 16 đến 20 sản phẩm. Do đó, bảng trên ghi Tổ 4 làm được 21 sản phẩm là không chính xác.
Vậy đội trưởng thống kê chưa đúng.
IV. Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu không ghép nhóm
1. Số trung bình cộng (Số trung bình)
Số trung bình (số trung bình cộng) của mẫu số liệu \({x_1},{x_2}, \ldots ,{x_n}\), kí hiệu là \(\bar x\), được tính bằng công thức:
\(\bar x = \dfrac{{{x_1} + {x_2} + \ldots + {x_n}}}{n}.\)
2. Trung vị
Sắp xếp mẫu số liệu theo thứ tự không giảm, ta được:
\({x_1} \le {x_2} \le \ldots \le {x_n}\)
Trung vị của mẫu, kí hiệu là \({M_e}\), là giá trị ở chính giữa dãy \({x_1},{x_2}, \ldots ,{x_n}\). Cụ thế:
- Nếu \(n = 2k + 1,k \in \mathbb{N}\), thì trung vị của mẫu \({M_e} = {x_{k + 1}}\).
- Nếu \(n = 2k,k \in \mathbb{N}\), thì trung vị của mẫu \({M_e} = \dfrac{1}{2}\left( {{x_k} + {x_{k + 1}}} \right)\).
3. Tứ phân vị
Để tìm các tứ phân vị của mẫu số liệu có \(n\) giá trị, ta làm như sau:
- Sắp xếp mẫu số liệu theo thứ tự không giảm.
- Tìm trung vị. Giá trị này là \({Q_2}\).
- Tìm trung vị của nửa số liệu bên trái \({Q_2}\) (không bao gồm \({Q_2}\) nếu \(n\) lẻ). Giá trị này là \({Q_1}\).
- Tìm trung vị của nửa số liệu bên phải \({Q_2}\) (không bao gồm \({Q_2}\) nếu \(n\) lẻ). Giá trị này là \({Q_3}\). \({Q_1},{Q_2},{Q_3}\) được gọi là các tứ phân vị của mẫu số liệu.
4. Mốt
Mốt của mẫu số liệu là giá trị có tần số lớn nhất trong bảng phân bố tần số và kí hiệu là \({M_0}\).
Ý nghĩa của mốt:
Mốt đặc trưng cho giá trị xuất hiện nhiều nhất trong mẫu.
V. Các số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm
1. Khoảng biến thiên. Khoảng tứ phân vị
Định nghĩa
- Trong một mẫu số liệu, khoảng biến thiên là hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó.
Ta có thể tính khoảng biến thiên \(R\) của mẫu số liệu theo công thức sau: \(R = {x_{{\rm{max }}}} - {x_{{\rm{min'}}}}\), trong đó \({x_{\max }}\) là giá trị lớn nhất, \({x_{\min }}\) là giá trị nhỏ nhất của mẫu số liệu đó.
- Giả sử \({Q_1},{Q_2},{Q_3}\) là tứ phân vị của mẫu số liệu. Ta gọi hiệu \({\Delta _Q} = {Q_3} - {Q_1}\) là khoảng tứ phân vị, của mẫu số liệu đó.
Chú ý: Một số tài liệu gọi khoảng biến thiên là biên độ và khoảng tứ phân vị là độ trải giữa.
2. Ý nghĩa của khoảng biến thiên và khoảng tứ phân vị
- Khoảng biến thiên đặc trưng cho độ phân tán của toàn bộ mẫu số liệu.
- Khoảng tứ phân vị đặc trımg cho độ phân tán của một nửa các số liệu, có giá trị thuộc đoạn từ \({Q_1}\) đển \({Q_3}\) trong mẫu.
- Khoảng tứ phân vị không bị ảnh hưởng bởi các giá trị rất lớn hoặc rất bé trong mẫu.

