I. Giá trị lượng giác của một góc
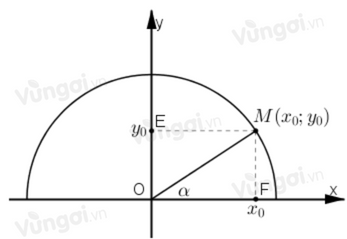
- Sin của góc \(\alpha \), kí hiệu là \(\sin \alpha \), được xác định bởi: \(\sin \alpha = {y_0}\);
- Côsin của góc \(\alpha \), kí hiệu là \(\cos \alpha \), được xác định bởi: \(\cos \alpha = {x_0}\);
- Tang của góc \(\alpha \), kí hiệu là tan \(\alpha \), được xác định bởi: \(\tan \alpha = \dfrac{{{y_0}}}{{{x_0}}}\left( {{x_0} \ne 0} \right)\);
- Côtang của góc \(\alpha \), kí hiệu là \(\cot \alpha \), được xác định bởi: \(\cot \alpha = \dfrac{{{x_0}}}{{{y_0}}}\left( {{y_0} \ne 0} \right)\).
Các số \(\sin \alpha ,\cos \alpha ,\tan \alpha ,\cot \alpha \) được gọi là các giá trị lượng giác của góc \(\alpha \).
Bảng giá trị lượng giác của một số góc đặc biệt:
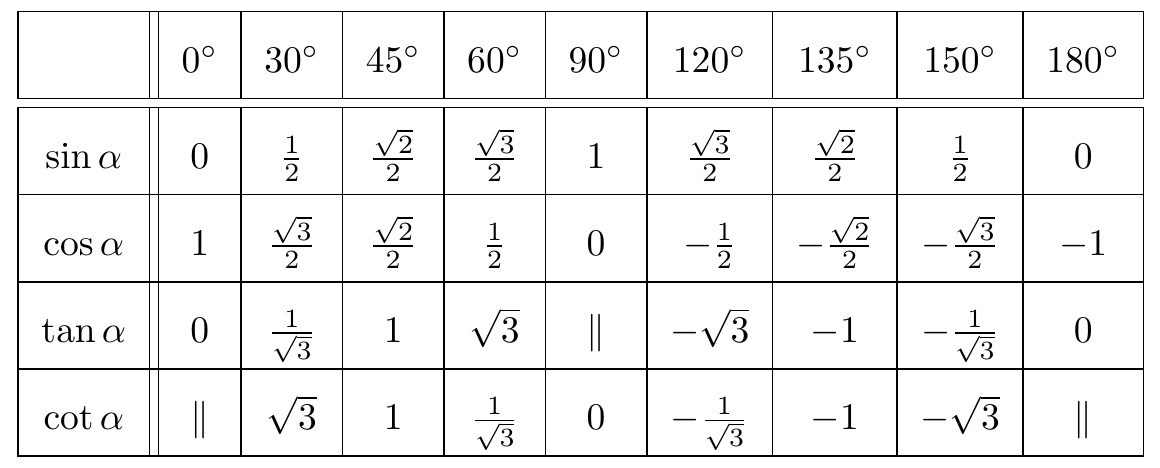
Một số hệ thức cơ bản:
\(\begin{array}{l}1)\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }}(\alpha \ne {90^0})\\2)\cot \alpha = \dfrac{{\cos \alpha }}{{\sin \alpha }}(\alpha \ne {0^0};{180^0})\\3)\tan \alpha .\cot \alpha = 1(\alpha \ne {0^0};{90^0};{180^0})\\4){\sin ^2}\alpha + {\cos ^2}\alpha = 1\\5)1 + {\tan ^2}\alpha = \dfrac{1}{{{{\cos }^2}\alpha }}(\alpha \ne {90^0})\\6)1 + {\cot ^2}\alpha = \dfrac{1}{{{{\sin }^2}\alpha }}(\alpha \ne {0^0};{180^0})\end{array}\)
II. Mối quan hệ giữa các giá trị lượng giác của hai góc bù nhau
Đối với hai góc bù nhau, \(\alpha \) và \({180^\circ } - \alpha \), ta có:
+ \(\sin \left( {{{180}^\circ } - \alpha } \right) = \sin \alpha \);
+ \(\cos \left( {{{180}^\circ } - \alpha } \right) = - \cos \alpha \);
+ \(\tan \left( {{{180}^\circ } - \alpha } \right) = - \tan \alpha \left( {\alpha \ne {{90}^\circ }} \right)\)
+ \(\cot \left( {{{180}^\circ } - \alpha } \right) = - \cot \alpha \left( {{0^\circ } < \alpha < {{180}^\circ }} \right)\).
Ví dụ:
Cho biết \(\sin {30^\circ } = \dfrac{1}{2};\cos {45^\circ } = \dfrac{{\sqrt 2 }}{2};\tan {60^\circ } = \sqrt 3 \).
Tính \(\sin {150^\circ };\cos {135^\circ };\tan {120^\circ }\)
Giải
\(\begin{array}{l}\sin {150^\circ } = \sin {30^\circ } = \dfrac{1}{2};\\\cos {135^\circ } = - \cos {45^\circ } = - \dfrac{{\sqrt 2 }}{2};\\\tan {120^\circ } = - \tan {60^\circ } = - \sqrt 3 \end{array}\)
Chú ý:
\(\begin{array}{l}\sin ({90^0} - \alpha ) = \cos \alpha & \\\cos ({90^0} - \alpha ) = \sin \alpha \,\\\tan ({90^0} - \alpha ) = \cot \alpha \\\cot ({90^0} - \alpha ) = \tan \alpha \end{array}\)
III. Sử dụng MTCT để tính giá trị lượng giác của một góc
- Để tính các giá trị lượng giác bằng MTCT, sau khi đưa máy về chế độ “độ” ta làm như sau:

- Tính góc khi biết một giá trị lượng giác của góc đó:


