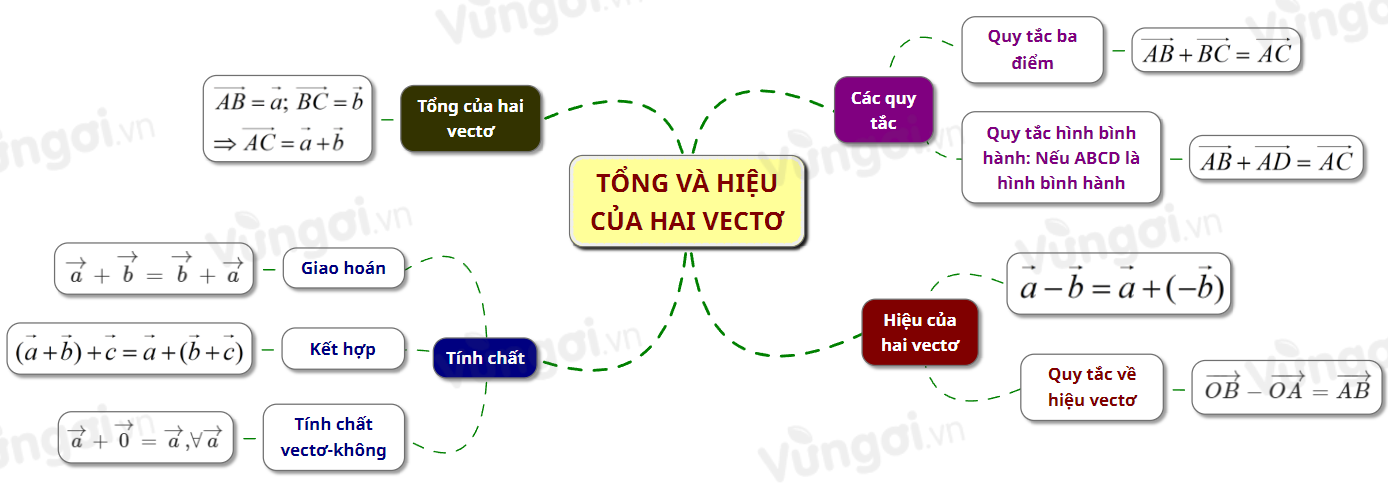
I. Sơ đồ tư duy Tổng và hiệu của hai vectơ
II. Tổng của hai vectơ
1. Tổng của hai vectơ
Cho hai vectơ \(\overrightarrow a \,;\,\overrightarrow b \). Từ điểm A tùy ý vẽ \(\overrightarrow {AB} = \overrightarrow a \) rồi từ B vẽ \(\overrightarrow {BC} = \overrightarrow b \).
Khi đó vectơ \(\overrightarrow {AC} \) được gọi là tổng của hai vectơ \(\overrightarrow a \,;\,\overrightarrow b \).
Kí hiệu \(\overrightarrow {AC} = \overrightarrow a + \overrightarrow b \)
2. Tính chất
+ Giao hoán : \(\overrightarrow a + \overrightarrow b = \overrightarrow b + \overrightarrow a \)
+ Kết hợp : \(\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right)\)
+ Tính chất vectơ – không: \(\overrightarrow a + \overrightarrow 0 = \overrightarrow a {\rm{, }}\forall \overrightarrow a \)
3. Các quy tắc
Quy tắc ba điểm:
Cho \(A,B,C\) tùy ý, ta có : \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Quy tắc hình bình hành:
Nếu \(ABCD\) là hình bình hành thì \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Chú ý: Ta có thể mở rộng quy tắc ba điểm cho n điểm \({A_1},\,{A_2},\,...,\,{A_n}\) thì \(\overrightarrow {{A_1}{A_2}} + \overrightarrow {{A_2}{A_3}} + ... + \overrightarrow {{A_{n - 1}}{A_n}} = \overrightarrow {{A_1}{A_n}} \)
III. Hiệu của hai vectơ
Hiệu của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là tổng của vectơ \(\overrightarrow a \) và vectơ đối của vectơ \(\overrightarrow b \).
Kí hiệu là \(\overrightarrow a - \overrightarrow b = \overrightarrow a + \left( { - \overrightarrow b } \right)\)
Chú ý:
Quy tắc về hiệu vectơ: Cho \(O,A,B\) tùy ý ta có: \(\overrightarrow {OB} - \overrightarrow {OA} = \overrightarrow {AB} \)

