Nhị thức Newton

I. Công thức nhị thức Newton

Chú ý:

Các hệ số trong khai triển nhị thức Newton ${\left( {a + b} \right)^n}$ với $n = 0;1;2;3;...$ được viết thành từng hàng và xếp thành bảng số như sau:

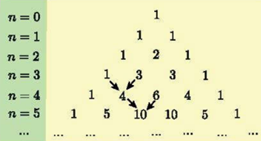
Bảng số trên được gọi là tam giác Pascal

II. Ví dụ

Ví dụ 1: Sử dụng công thức nhị thức Newton, khai triển biểu thức:

1. a) ${(x + 3)^4}$
2. b) ${(1 - x)^5}$

Giải

a)

Theo công thức nhị thức Newton, ta có

${(x + 3)^4} = 1.{x^4} + 4.{x^3}.3 + 6.{x^2}{.3^2} + 4.x{.3^3} + {1.3^4}$

$= {x^4} + 4.3.{x^3} + 6.9.{x^2} + 4.27.x + 81$

$= {x^4} + 12{x^3} + 54{x^2} + 108x + 81$

b)

Theo công thức nhị thức Newton, ta có

$\begin{array}{*{20}{l}}{{{\left( {1 - x} \right)}^5} = 1 + 5.\left( { - x} \right) + 10.{{\left( { - x} \right)}^2} + 10.{{\left( { - x} \right)}^3} + 5.{{\left( { - x} \right)}^2} + 1.{{\left( { - x} \right)}^5}}\\{ = 1 - 5x + 10{x^2} - 10{x^3} + 5{x^4} - {x^5}.}\end{array}$

Ví dụ 3

Khai triển và rút gọn biểu thức: ${(1 + \sqrt 2 )^5} + {(1 - \sqrt 2 )^5}$.

Giải

Áp dụng công thức nhị thức Newton, ta có

${(1 + \sqrt 2 )^5} = 1 + 5.\sqrt 2 + 10.{(\sqrt 2 )^2} + 10.{(\sqrt 2 )^3} + 5.{(\sqrt 2 )^4} + 1.{(\sqrt 2 )^5}$

${(1 - \sqrt 2 )^5} = 1 + 5.( - \sqrt 2 ) + 10.{( - \sqrt 2 )^2} + 10.{( - \sqrt 2 )^3} + 5.{( - \sqrt 2 )^4} + 1.{( - \sqrt 2 )^5}$

Từ đó:

${(1 + \sqrt 2 )^5} + {(1 - \sqrt 2 )^5} = 2\left[ {1 + 10 \cdot {{(\sqrt 2 )}^2} + 5 \cdot {{(\sqrt 2 )}^4}} \right] = 2(1 + 10 \cdot 2 + 5 \cdot 4) = 82.$