I. Nguyên lí xác suất bé
Qua thực tế người ta thấy rằng một biến cố có xác suất rất bé thì sẽ không xảy ra khi ta thực hiện một phép thử hay một vài phép thử.
Nguyên lí xác suất bé:
Nếu một biến cố có xác suất rất bé thì trong một phép thử biến cố đó sẽ không xảy ra.
Chú ý: Trong thực tế, xác suất của một biến cố được coi là bé phụ thuộc vào từng trường hợp cụ thể. Chẳng hạn, xác suất một chiếc điện thoại bị lỗi kĩ thuật là 0,001 được coi là rất bé, nhưng nếu xác suất cháy nổ động cơ của một máy bay là 0,001 thì xác suất này không được coi là rất bé.
II. Sử dụng phương pháp tổ hợp
Trong nhiều bài toán, để tính số phần tử của không gian mẫu, của các biến cố, ta thường sử dụng các quy tắc đếm, các công thức tính số hoán vị, chỉnh hợp và tổ hợp.
Ví dụ: Một tổ trong lớp \(10\;{\rm{A}}\) có 10 học sinh trong đó có 6 học sinh nam và 4 học sinh nữ. Giáo viên chọn ngẫu nhiên 6 học sinh trong tổ đó để tham gia đội tình nguyện Mùa hè xanh. Tính xác suất của biến cố sau:
C: "6 học sinh được chọn đều là nam";
Giải
Không gian mẫu là tập tất cả các tập con gồm 6 học sinh trong 10 học sinh. Vậy
\(n(\Omega ) = C_{10}^6 = 210.\)
Tập C chỉ có một phần tử là tập 6 học sinh nam
Vậy \(n(C) = 1\), do đó \(P(C) = \dfrac{1}{{210}}\).
III. Sử dụng sơ đồ hình cây
Trong một số bài toán, phép thử \(T\) được hình thành từ một vài phép thử, chẳng hạn: gieo xúc xắc liên tiếp bốn lần; lấy ba viên bi, mỗi viên từ một hộp;... Khi đó ta sử dụng sơ đồ hình cây để có thể mô tả đầy đủ, trực quan không gian mẫu và biến cố cần tính xác suất.
Ví dụ: Có ba chiếc hộp. Hộp I có chứa ba viên bi: 1 viên màu đỏ, 1 viên màu xanh và 1 viên màu vàng. Hộp II chứa hai viên bi: 1 viên màu xanh và 1 viên màu vàng. Hộp III chứa hai viên bi: 1 viên màu đỏ và 1 viên màu xanh. Từ mỗi hộp ta lấy ngẫu nhiên một viên bi.
a) Vẽ sơ đồ hình cây để mô tả các phần tử của không gian mẫu.
b) Tính xác suất để trong ba viên bi lấy ra có đúng một viên bi màu xanh.
Giải
a) Kí hiệu Đ, X, V tương ứng là viên bi màu đỏ, màu xanh và màu vàng.
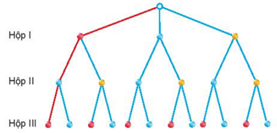
Các kết quả có thể là: ĐXĐ, ĐXX, ĐVĐ, ĐVX, XXĐ, XXX, XVĐ, XVX, VXĐ, VXX, VVĐ, VVX.
Do đó Q = {ĐXĐ; ĐXX; ĐVĐ; ĐVX; XXĐ; XXX; XVĐ; XVX; VXĐ; VXX; VVĐ; VVX}.
Vậy \(n(\Omega ) = 12\).
b) Gọi \(K\) là biến cố: "Trong ba viên bi lấy ra có đúng một viên bi màu xanh". Ta có K={ĐVĐ; ĐVX; XVĐ; VXĐ; VVX}.
Vậy \(n(K) = 5\). Từ đó
\(P(K) = \dfrac{{n(K)}}{{n(\Omega )}} = \dfrac{5}{{12}}{\rm{. }}\)
IV. Xác suất của biến cố đối
Cho \(E\) là một biến cố. Xác suất của biến cố \(\bar E\) liên hệ với xác suất của \(E\) bởi công thức sau:
\(P(\bar E) = 1 - P(E).\)
Chú ý: Trong một số bài toán, nếu tính trực tiếp xác suất của biến cố gặp khó khăn, ta có thể tính gián tiếp bằng cách tính xác suất của biến cố đối của nó.
Ví dụ: Chọn ngẫu nhiên hai số từ tập \(\{ 1;2; \ldots ;9\} \). Gọi H là biến cố: "Trong hai số được chọn có ít nhất một số chẵn".
a) Mô tả không gian mẫu.
b) Biến cố \(\bar H\) là tập con nào của không gian mẫu?
c) Tính \(P(\bar H)\) và \(P(H)\).
Giải
a) Không gian mẫu là tập tất cả các tập con có 2 phần tử của tập \(\{ 1;2; \ldots ;8;9\} \).
b) Biến cố \(\bar H\) : "Cả hai số được chọn đều là số lẻ". Khi đó \(\bar H\) là tập tất cả các tập con có 2 phần tử của tập số lẻ \(\{ 1;3;5;7;9\} \).
c) Ta có \(n(\Omega ) = C_9^2 = 36,n(\bar H) = C_5^2 = 10\). Vậy \(P(\bar H) = \dfrac{{10}}{{36}} = \dfrac{5}{{18}}\).
Từ đó \(P(H) = 1 - P(\bar H) = 1 - \dfrac{5}{{18}} = \dfrac{{13}}{{18}}\).
