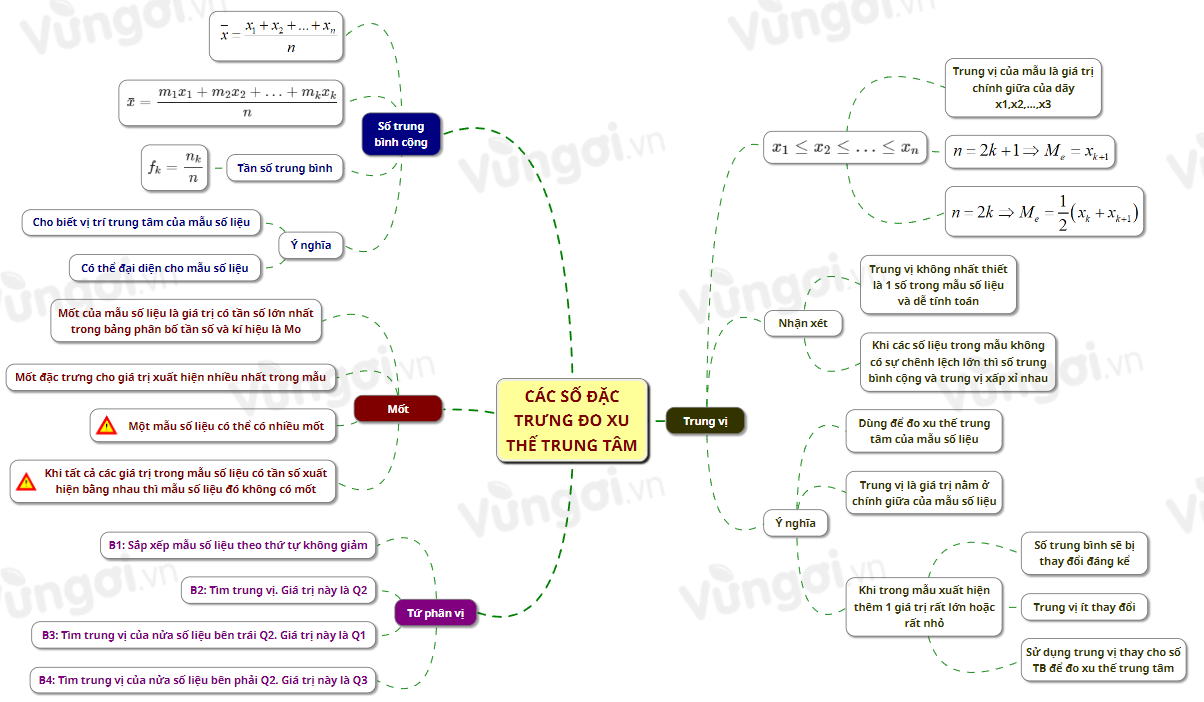
I. Sơ đồ tư duy các số đặc trưng đo xu thế trung tâm
II. Số trung bình cộng (Số trung bình)
Số trung bình (số trung bình cộng) của mẫu số liệu \({x_1},{x_2}, \ldots ,{x_n}\), kí hiệu là \(\bar x\), được tính bằng công thức:
\(\bar x = \dfrac{{{x_1} + {x_2} + \ldots + {x_n}}}{n}.\)
Chú ý.
- Trong trường hợp mẫu số liệu cho dưới dạng bảng tần số thì số trung bình được tính theo công thức:
\(\bar x = \dfrac{{{m_1}{x_1} + {m_2}{x_2} + \ldots + {m_k}{x_k}}}{n},\)
trong đó \({m_k}\) là tần số của giá trị \({x_k}\) và \(n = {m_1} + {m_2} + \ldots + {m_k}\). Ta gọi \(n\) là cỡ mẫu.
- Nếu kí hiệu \({f_k} = \dfrac{{{n_k}}}{n}\) là tần số tương đối (hay còn gọi là tần suất) của \({x_k}\) trong mẫu số liệu thì số trung bình còn có thể biểu diễn là: \(\bar x = {f_1}{x_1} + {f_2}{x_2} + \ldots + {f_k}{x_k}\).
Ý nghĩa:
- Số trung bình là giá trị trung bình cộng của các số trong mẫu số liệu, nó cho biết vị trí trung tâm của mẫu số liệu và có thể dùng để đại diện cho mẫu số liệu.
- Khi các số liệu trong mẫu ít sai lệch với số trung bình cộng, ta có thể giải quyết được vấn đề trên bằng cách lấy số trung bình cộng làm đại diện cho mẫu số liệu.
III. Trung vị
Sắp xếp mẫu số liệu theo thứ tự không giảm, ta được:
\({x_1} \le {x_2} \le \ldots \le {x_n}\)
Trung vị của mẫu, kí hiệu là \({M_e}\), là giá trị ở chính giữa dãy \({x_1},{x_2}, \ldots ,{x_n}\). Cụ thế:
- Nếu \(n = 2k + 1,k \in \mathbb{N}\), thì trung vị của mẫu \({M_e} = {x_{k + 1}}\).
- Nếu \(n = 2k,k \in \mathbb{N}\), thì trung vị của mẫu \({M_e} = \dfrac{1}{2}\left( {{x_k} + {x_{k + 1}}} \right)\).
Nhận xét:
- Trung vị không nhất thiết là một số trong mẫu số liệu và dễ tính toán.
- Khi các số liệu trong mẫu không có sự chênh lệch lớn thì số trung bình cộng và trung vị xấp xỉ nhau.
Ý nghĩa của trung vị
+ Trung vị được dùng để đo xu thế trung tâm của mẫu số liệu.
+ Trung vị là giá trị nằm ở chính giữa của mẫu số liệu theo nghĩa: luôn có ít nhất \(50\% \) số liệu trong mẫu lớn hơn hoặc bằng trung vị và ít nhất \(50\% \) số liệu trong mẫu nhỏ hơn hoặc bằng trung vị.
+ Khi trong mẫu xuất hiện thêm một giá trị rất lớn hoặc rất nhỏ thì số trung bình sẽ bị thay đổi đáng kể nhưng trung vị thì ít thay đổi.
$\Rightarrow$ Sử dụng trung vị thay cho số trung bình để đo xu thế trung tâm.
IV. Tứ phân vị
Để tìm các tứ phân vị của mẫu số liệu có \(n\) giá trị, ta làm như sau:
- Sắp xếp mẫu số liệu theo thứ tự không giảm.
- Tìm trung vị. Giá trị này là \({Q_2}\).
- Tìm trung vị của nửa số liệu bên trái \({Q_2}\) (không bao gồm \({Q_2}\) nếu \(n\) lẻ). Giá trị này là \({Q_1}\).
- Tìm trung vị của nửa số liệu bên phải \({Q_2}\) (không bao gồm \({Q_2}\) nếu \(n\) lẻ). Giá trị này là \({Q_3}\). \({Q_1},{Q_2},{Q_3}\) được gọi là các tứ phân vị của mẫu số liệu.
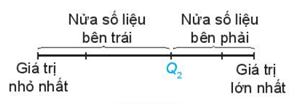
Chú ý: \({Q_1}\) được gọi là tứ phân vị thứ nhất hay tứ phân vị dưới, \({Q_3}\) được gọi là tứ phân vị thứ ba hay tứ phân vị trên.
Ý nghĩa: Các điểm \({Q_1},{Q_2},{Q_3}\) chia mẫu số liệu đã sắp xếp theo thứ tự từ nhỏ đến lớn thành bốn phần, mỗi phần đều chứa \(25\% \) giá trị.
Ví dụ:
Tìm các tứ phân vị của mẫu số liệu sau:
5 ; 13 ; 5 ; 7 ; 10 ; 2 ; 3
Giải
Sắp xếp lại mẫu số liệu theo thứ tự không giảm, ta được: 2 ; 3 ; 5 ; 5 ; 7 ; 10 ; 13
Vì cỡ mẫu là \(n = 7\), là số lẻ, nên:
- Tứ phân vị thứ hai là \({Q_2} = 5\).
- Tứ phân vị thứ nhất là trung vị của mẫu: 2 ; 3 ; 5. Do đó \({Q_1} = 3\).
- Tứ phân vị thứ ba là trung vị của mẫu: 7 ; 10 ; 13. Do đó \({Q_3} = 10\).
V. Mốt
Mốt của mẫu số liệu là giá trị có tần số lớn nhất trong bảng phân bố tần số và kí hiệu là \({M_0}\).
Ý nghĩa của mốt:
Mốt đặc trưng cho giá trị xuất hiện nhiều nhất trong mẫu.
Chú ý: Một mẫu số liệu có thể có nhiều mốt. Khi tất cả các giá trị trong mẫu số liệu có tần số xuất hiện bằng nhau thì mẫu số liệu đó không có mốt.

