Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Xét tam giác $DEF$  và tam giác $HKG$  có $\widehat D = \widehat H$, $\widehat E = \widehat K$, $DE = HK,$ do đó $\Delta DEF = \Delta HKG$(g.C.g).

Do đó $\widehat G = \widehat F = {80^0}$ (hai góc tương ứng).

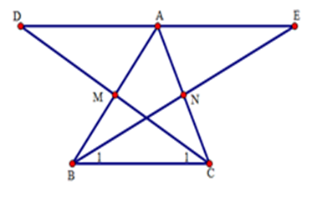
(I) Xét $\Delta AMD$ và $\Delta BMC$ có: $DM = MC\left( {gt} \right);$ $\widehat {BMC} = \widehat {AMD}$ (hai góc đối đỉnh); $AM = BM\left( {gt} \right),$ nên $\Delta AMD = \Delta BMC$(c.g.c).

(II) Xét $\Delta ANE$ và $\Delta CNB$ có: $AN = NC\left( {gt} \right);$ $\widehat {ANE} = \widehat {CNB}$(hai góc đối đỉnh), $NB = NE\left( {gt} \right),$ do đó

$\Delta CNB = \Delta ANE$(c.g.c).

(III) Do $\Delta AMD = \Delta BMC$ nên $\widehat D = \widehat {{C_1}}$(hai góc tương ứng).

Mà hai góc này ở vị trí so le trong nên $AD//BC.$

Do  $\Delta CNB = \Delta ANE$nên $\widehat E = \widehat {{B_1}}$(hai góc tương ứng).

Mà hai góc này ở vị trí so le trong nên $AE//BC.$

Như vậy qua $A$  có hai đường thẳng $AD,AE$ cùng song song với $BC.$  

Do đó $D,A,E$ thẳng hàng. (1)

(IV) Ta có: $AD = BC$ (do $\Delta AMD = \Delta BMC$); $AE = BC$ (do $\Delta CNB = \Delta ANE$) nên $AD = AE\left( 2 \right)$

Từ (1) và (2) suy ra $A$  là trung điểm của $DE.$

Vậy cả (I); (II); (III); (IV) đều đúng.

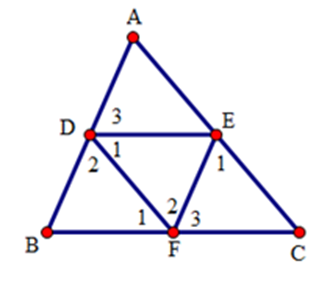
Xét tam giác $DEF$  và tam giác $FBD$  có:

$\widehat {{D_1}} = \widehat {{F_1}}$ (hai góc so le trong).

$DF$ là cạnh chung

$\widehat {{F_2}} = \widehat {{D_2}}$ (hai góc so le trong).

Vậy $\Delta DEF = \Delta FBD\,\,\,(g.c.g)$

Suy ra $EF = BD$ (hai cạnh tương ứng)

 Mà $AD = BD$ nên $EF = AD$

Ta có : $\widehat {{F_3}} = \widehat B$ (hai góc đồng vị); $\widehat {{D_3}} = \widehat B$ (hai góc đồng vị)

 $\Rightarrow \widehat {{D_3}} = \widehat {{F_3}}\left( { = \widehat B} \right).$.

Xét tam giác $ADE$ và tam giác $EFC$  có:

$\widehat {{D_3}} = \widehat {{F_3}}$(cmt)

$\widehat A = \widehat {{E_1}}$(hai góc đồng vị)

$AD = EF\left( {cmt} \right)$

 $\Rightarrow \Delta ADE = \Delta EFC\,\,\,(g.c.g).$  (1)

Tương tự ta chứng minh được $\Delta EFC = \Delta DBF\,\,\,(g.c.g)$     (2)

Từ (1) và (2) suy ra $\Delta ADE = \Delta EFC = \Delta DBF$                      (3)

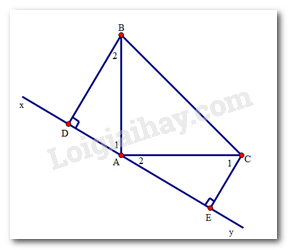
Ta có: ${\widehat A_1} + {\widehat A_2} = {90^0}\,\,\,\left( {do\,\,\,\widehat {BAC} = {{90}^0}} \right)$

Mà ${\widehat A_1} + {\widehat B_2} = {90^0}$ (vì tam giác $ABD$  vuông tại $D.$)

$\Rightarrow {\widehat B_2} = {\widehat A_2}$  (cùng phụ với ${\widehat A_1}$).

Lại có ${\widehat A_2} + {\widehat C_1} = {90^0}$ (vì tam giác $ACE$  vuông tại $E$ )

$\Rightarrow {\widehat A_1} = {\widehat C_1}$ (cùng phụ với ${\widehat A_2}$).

Xét hai tam giác $BDA$  và $AEC$  có:

$\widehat {{B_2}} = \widehat {{A_2}}$; $AB = AC$ (gt) và$\widehat {{A_1}} = \widehat {{C_1}}$ (cmt)

$\Rightarrow \Delta BA{\rm{D}} = \Delta ACE$ (g.c.g)

$\Rightarrow$ $BD = AE$ (hai cạnh tương ứng), $CE = AD$ (hai cạnh tương ứng).

Do đó $DE = AD + AE = CE + BD.$

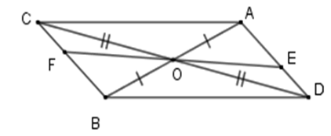
 * Xét tam giác $OBC$ và $OAD$ có

+ $OA = OB\,\left( {gt} \right)$

+ $\widehat {AOD} = \widehat {BOC}$ (đối đỉnh)

+ $OC = OD\left( {gt} \right)$

Suy ra $\Delta OAD = \Delta OBC\left( {c - g - c} \right)$ nên $\widehat {OAD} = \widehat {OBC}$  (hai góc tương ứng)

* Xét tam giác $OBF$ và $OAE$ có

+ $OA = OB\,\left( {gt} \right)$

+ $\widehat {OAD} = \widehat {OBC}$ (cmt)

+ $BF = AE\left( {gt} \right)$

Suy ra $\Delta OBF = \Delta OAE\left( {c - g - c} \right)$ nên $OE = OF$ (hai cạnh tương ứng) và $\widehat {AOE} = \widehat {FOB}$  (hai góc tương ứng)

Mà $\widehat {FOB} + \widehat {FOA} = 180^\circ$ (hai góc kề bù) nên $\widehat {FOA} + \widehat {AOE} = 180^\circ$

Suy ra ba điểm $F;\,O;E$ thẳng hàng và $OE = OF$ nên $O$ là trung điểm của $EF \Rightarrow EF = 2.OE = 4\,cm.$

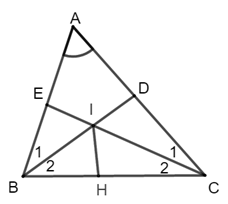
Vì $BD$ là tia phân giác của $\widehat {ABC}$ nên $\widehat {{B_1}} = \widehat {{B_2}} = \dfrac{1}{2}\widehat {ABC}$

Vì $CE$ là tia phân giác của $\widehat {ACB}$ nên $\widehat {{C_1}} = \widehat {{C_2}} = \dfrac{1}{2}\widehat {ACB}$

Xét $\Delta ABC$ có: $\widehat A + \widehat {ABC} + \widehat {ACB} = 180^\circ$ (tổng ba góc của một tam giác bằng $180^\circ$)

Mà $\widehat A = 60^\circ$ nên $\widehat {ABC} + \widehat {ACB} = 180^\circ  - \widehat A = 180^\circ  - 60^\circ  = 120^\circ$

Ta lại có: $\widehat {{B_2}} + \widehat {{C_2}} = \dfrac{1}{2}\widehat {ABC} + \dfrac{1}{2}\widehat {ACB} = \dfrac{1}{2}(\widehat {ABC} + \widehat {ACB}) = \dfrac{1}{2}.120^\circ  = 60^\circ$

Xét $\Delta BIC$ có $\widehat {BIC} + \widehat {{B_2}} + \widehat {{C_2}} = 180^\circ$ (tổng ba góc của một tam giác bằng $180^\circ$)

Mà $\widehat {{B_2}} + \widehat {{C_2}} = 60^\circ$ nên $\widehat {BIC} = 180^\circ  - (\widehat {{B_2}} + \widehat {{C_2}}) = 180^\circ  - 60^\circ  = 120^\circ$

Mặt khác: $\widehat {BIC} + \widehat {BIE} = 180^\circ$ (hai góc kề bù) $\Rightarrow \widehat {BIE} = 180^\circ  - \widehat {BIC} = 180^\circ  - 120^\circ  = 60^\circ$

Khi đó $\widehat {CID} = \widehat {BIE} = 60^\circ$ (hai góc đối đỉnh)  $(1)$

Kẻ tia phân giác của $\widehat {BIC}$ cắt $BC$ tại $H$

Suy ra $\widehat {BIH} = \widehat {HIC} = \dfrac{1}{2}.\widehat {BIC} = \dfrac{1}{2}.120^\circ  = 60^\circ$$(2)$

Từ $(1)$ và $(2)$ suy ra $\widehat {CID} = \widehat {BIE} = \widehat {BIH} = \widehat {HIC}$

Xét tam giác $BIE$ và tam giác $BIH$ có:

$\widehat {{B_1}} = \widehat {{B_2}}$ (cmt)

$BI$ là cạnh chung

$\widehat {BIE} = \widehat {BIH}$ (cmt)

$\Rightarrow \Delta BIE = \Delta BIH \,(g.c.g) \Rightarrow IE = IH$ (hai cạnh tương ứng) $(3)$

Xét tam giác $CID$ và tam giác $CIH$ có:

$\widehat {{C_1}} = \widehat {{C_2}}$ (cmt)

$CI$ là cạnh chung

$\widehat {CID} = \widehat {HIC}$ (cmt)

$\Rightarrow \Delta CID = \Delta CIH \,(g.c.g) \Rightarrow ID = IH$ (hai cạnh tương ứng) $(4)$

Từ $(3)$ và $(4)$ suy ra $ID = IE = 2cm$

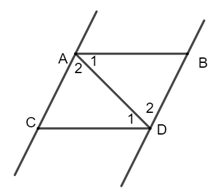
Kẻ đoạn thẳng $AD$

Vì $AB//CD$ (gt) nên $\widehat {{A_1}} = \widehat {{D_1}}$ (hai góc so le trong)

Vì $AC//BD$ (gt) nên $\widehat {{A_2}} = \widehat {{D_2}}$ (hai góc so le trong)

Xét tam giác $ABD$ và tam giác $DCA$ có:

$\widehat {{A_1}} = \widehat {{D_1}}$ (cmt)

$AD$ là cạnh chung

$\widehat {{A_2}} = \widehat {{D_2}}$ (cmt)

$\Rightarrow \Delta ABD = \Delta DCA\,(g.c.g) \Rightarrow AB = CD$ (hai cạnh tương ứng); $AC = BD$ (hai cạnh tương ứng)

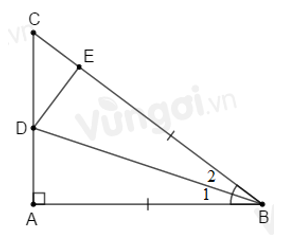
Xét $\Delta ABD$ và $\Delta EBD$ có:

$BA = BE$ (gt)

$\widehat {{B_1}} = \widehat {{B_2}}$ (vì $BD$ là tia phân giác $\widehat {ABC}$)

$BD$ cạnh chung

$\Rightarrow \Delta ABD{\rm{ }} = \Delta EBD\,(c.g.c)$

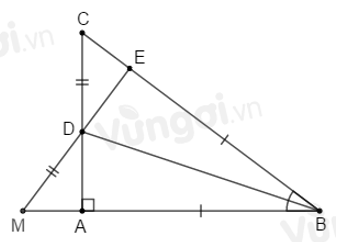
Sử dụng kết quả câu trước $\Delta ABD{\rm{ }} = \Delta EBD$ suy ra $DE = DA$ (hai cạnh tương ứng). Nối $AM.$

Xét $\Delta ADM$ và $\Delta EDC$ có:

$DA = DE$ (chứng minh trên)

$\widehat {ADM} = \widehat {EDC}$ (hai góc đối đỉnh)

$DM = DC\,(gt)$

$\Rightarrow \Delta ADM = \Delta EDC\,(c.g.c)$

$\Rightarrow AM = EC$ (hai cạnh tương ứng bằng nhau).

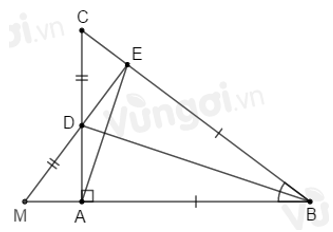
Sử dụng kết quả câu trước $\Delta ADM = \Delta EDC$ suy ra $AD = ED;\,AM = EC$ (các cạnh tương ứng).

Ta có: $AD = ED\,\,\,\,(1)$

           $DC = DM\,\,\,(2)$

Cộng (1) và (2) theo vế với vế ta được: $AD + DC = ED + DM$ hay $AC = EM$.

Xét $\Delta AEC$ và $\Delta EAM$ có:

$AE$ cạnh chung

$EC = AM\,(cmt)$

$AC = EM\,(cmt)$

$\Rightarrow \Delta AEC = \Delta EAM\,(c.c.c)$

$\Rightarrow \widehat {AEC} = \widehat {EAM}$ (hai góc tương ứng).

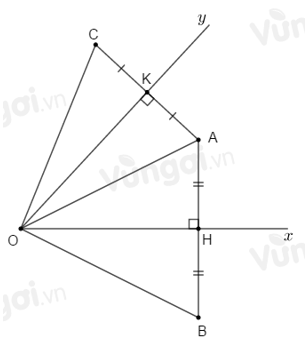
Xét $\Delta OAH$ và $\Delta OBH$ có:

$OH$ cạnh chung

$\widehat {OHA} = \widehat {OHB} = {90^o}$

$HA = HB\,(gt)$

$\Rightarrow \Delta OAH = \Delta OBH\,(c.g.c)$

$\Rightarrow OA = OB$ (hai cạnh tương ứng)     (1)

Xét $\Delta OAK$ và $\Delta OCK$ có:

$OK$ cạnh chung

$\widehat {OKA} = \widehat {OKC} = {90^o}$

$KA = KC\,(gt)$

$\Rightarrow \Delta OAK = \Delta OCK\,(c.g.c)$

$\Rightarrow OA = OC$ (hai cạnh tương ứng)     (2)

Từ (1) và (2) suy ra $OA = OB = OC.$

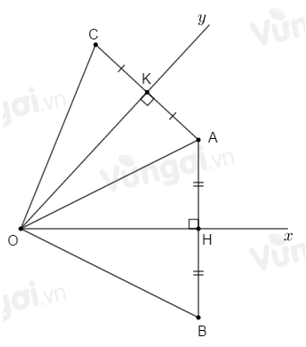
Sử dụng kết quả câu trước ta có: $\Delta OAH = \Delta OBH$, $\Delta OAK = \Delta OCK$.

Vì $\Delta OAH = \Delta OBH$ suy ra $\widehat {BOH} = \widehat {AOH}$ (hai góc tương ứng).

Vì $\Delta OAK = \Delta OCK$ suy ra $\widehat {AOK} = \widehat {COK}$ (hai góc tương ứng).

Ta có $\widehat {BOC} = \widehat {BOA} + \widehat {AOC}$

$\Rightarrow \widehat {BOC} = \widehat {BOH} + \widehat {AOH} + \widehat {AOK} + \widehat {COK}$

$\Rightarrow \widehat {BOC} = 2\widehat {AOH} + 2\widehat {AOK}$ (vì $\widehat {BOH} = \widehat {AOH}$ và $\widehat {AOK} = \widehat {COK}$)

$\Rightarrow \widehat {BOC} = 2\left( {\widehat {AOH} + \widehat {AOK}} \right) = 2\widehat {xOy} = 2\alpha .$