Cho tam giác $ABC$ có $M,N$ lần lượt là trung điểm của $AB,AC.$ Trên tia đối của tia $MC$ lấy $D$ sao cho $MD = MC$ . Trên tia đối của tia $NB$ lấy điểm $E$ sao cho $NE = NB.$
(I) \(\Delta AMD = \Delta BMC\)
(II) \(\Delta ANE = \Delta CNB\)
(III) $A,D,E$ thẳng hàng
(IV) $A$ là trung điểm của đoạn thẳng $DE$
Số khẳng định đúng trong các khẳng định trên là
Trả lời bởi giáo viên
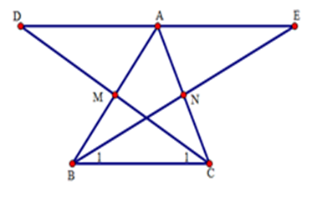
(I) Xét \(\Delta AMD\) và \(\Delta BMC\) có: $DM = MC\left( {gt} \right);$ \(\widehat {BMC} = \widehat {AMD}\) (hai góc đối đỉnh); $AM = BM\left( {gt} \right),$ nên \(\Delta AMD = \Delta BMC\)(c.g.c).
(II) Xét \(\Delta ANE\) và \(\Delta CNB\) có: $AN = NC\left( {gt} \right);$ \(\widehat {ANE} = \widehat {CNB}\)(hai góc đối đỉnh), $NB = NE\left( {gt} \right),$ do đó
\(\Delta CNB = \Delta ANE\)(c.g.c).
(III) Do \(\Delta AMD = \Delta BMC\) nên \(\widehat D = \widehat {{C_1}}\)(hai góc tương ứng).
Mà hai góc này ở vị trí so le trong nên $AD//BC.$
Do \(\Delta CNB = \Delta ANE\)nên \(\widehat E = \widehat {{B_1}}\)(hai góc tương ứng).
Mà hai góc này ở vị trí so le trong nên $AE//BC.$
Như vậy qua $A$ có hai đường thẳng $AD,AE$ cùng song song với $BC.$
Do đó $D,A,E$ thẳng hàng. (1)
(IV) Ta có: $AD = BC$ (do \(\Delta AMD = \Delta BMC\)); $AE = BC$ (do \(\Delta CNB = \Delta ANE\)) nên $AD = AE\left( 2 \right)$
Từ (1) và (2) suy ra $A$ là trung điểm của $DE.$
Vậy cả (I); (II); (III); (IV) đều đúng.
Hướng dẫn giải:
(I), (II) Dựa vào trường hợp bằng nhau thứ hai của tam giác để chứng minh các tam giác bằng nhau
(III) Để chứng minh ba điểm $A,D,E$ thẳng hàng ta chứng minh $A$ có hai đường thẳng $AD,AE$ cùng song song với $BC.$
(IV) Để chứng minh $A$ là trung điểm của $DE$ ta chứng minh $AD$ và $AE$ cùng bằng $BC$ do đó chúng bằng nhau.

