Cho điểm \(A\) nằm trong góc nhọn \(xOy.\) Vẽ \(AH\) vuông góc với \(Ox,\) trên tia đối của tia \(HA\) lấy điểm \(B\) sao cho \(HB = HA.\) Vẽ \(AK\) vuông góc với \(Oy,\) trên tia đổi của tia \(KA\) lấy điểm \(C\) sao cho \(KC = KA.\)
Biết \(\widehat {xOy} = \alpha .\) Tính \(\widehat {BOC}.\)
Trả lời bởi giáo viên
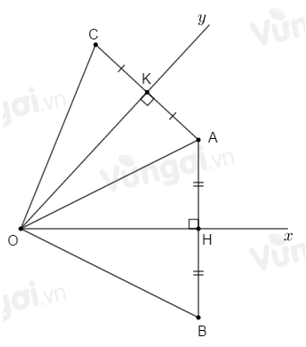
Sử dụng kết quả câu trước ta có: \(\Delta OAH = \Delta OBH\), \(\Delta OAK = \Delta OCK\).
Vì \(\Delta OAH = \Delta OBH\) suy ra \(\widehat {BOH} = \widehat {AOH}\) (hai góc tương ứng).
Vì \(\Delta OAK = \Delta OCK\) suy ra \(\widehat {AOK} = \widehat {COK}\) (hai góc tương ứng).
Ta có \(\widehat {BOC} = \widehat {BOA} + \widehat {AOC}\)
\( \Rightarrow \widehat {BOC} = \widehat {BOH} + \widehat {AOH} + \widehat {AOK} + \widehat {COK}\)
\( \Rightarrow \widehat {BOC} = 2\widehat {AOH} + 2\widehat {AOK}\) (vì \(\widehat {BOH} = \widehat {AOH}\) và \(\widehat {AOK} = \widehat {COK}\))
\( \Rightarrow \widehat {BOC} = 2\left( {\widehat {AOH} + \widehat {AOK}} \right) = 2\widehat {xOy} = 2\alpha .\)
Hướng dẫn giải:
Sử dụng kết quả câu trước ta có: \(\Delta OAH = \Delta OBH\), \(\Delta OAK = \Delta OCK\). Từ đó suy ra \(\widehat {BOH} = \widehat {AOH}\), \(\widehat {AOK} = \widehat {COK}\) (các cặp góc tương ứng), sau đó biến đổi để tìm được số đo của \(\widehat {BOC}.\)

