Cho $A = \left\{ {1,2,3} \right\}$. Hãy chọn câu trả lời đúng trong các câu sau:
Tập $A = \left\{ {1,2,3} \right\}$ có \(3\) phần tử nên \(A\) có \({2^3} = 8\) tập hợp con.
Tìm $m$ để \(\left( { - \infty ;1} \right] \cap \left( {m;m + 1} \right) = \emptyset \)
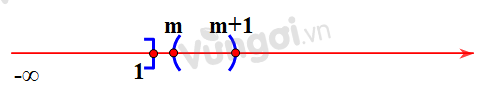
Để \(\left( { - \infty ;1} \right] \cap \left( {m;m + 1} \right) = \emptyset \) thì hai tập số \(\left( { - \infty ;1} \right]\) và \(\left( {m;m + 1} \right)\) phải rời nhau trên \(R\).
Khi đó tập \(\left( {m;m + 1} \right)\) khi biểu diễn trên trục số sẽ phải nằm về bên phải tập \(\left( { - \infty ;1} \right]\).
Điều đó chỉ xảy ra khi \(1 \le m < m + 1 \Leftrightarrow m \ge 1\).
Cho tập $A = \left\{ {1;2;3;4;5;6} \right\}$. Số các tập con khác nhau của $A$ gồm hai phần tử là:
Các tập con gồm hai phần tử của \(A\) là:
\(\begin{array}{l}\left\{ {1;2} \right\},\left\{ {1;3} \right\},\left\{ {1;4} \right\},\left\{ {1;5} \right\},\left\{ {1;6} \right\},\left\{ {2;3} \right\},\left\{ {2;4} \right\},\left\{ {2;5} \right\},\left\{ {2;6} \right\},\\\left\{ {3;4} \right\},\left\{ {3;5} \right\},\left\{ {3;6} \right\},\left\{ {4;5} \right\},\left\{ {4;6} \right\},\left\{ {5;6} \right\}\end{array}\)
Vậy có \(15\) tập hợp con của \(A\) gồm hai phần tử.
Tìm $m$ để \(\left( {0;1} \right) \cap \left( {m;m + 3} \right) = \emptyset \)
\(\left( {0;1} \right) \cap \left( {m;m + 3} \right) = \emptyset \Leftrightarrow \left[ \begin{array}{l}0 < 1 \le m < m + 3\\m < m + 3 \le 0 < 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m \ge 1\\m \le - 3\end{array} \right.\).
Số các tập con $3$ phần tử có chứa $\alpha ,\pi $ của \(C = \left\{ {\alpha ,\beta ,\xi ,\pi ,\rho ,\eta ,\gamma ,\sigma ,\omega ,\tau } \right\}\) là:
Các tập con có \(3\) phần tử của \(C\) là:
\(\left\{ {\alpha ,\pi ,\beta } \right\},\left\{ {\alpha ,\pi ,\xi } \right\},\left\{ {\alpha ,\pi ,\rho } \right\},\left\{ {\alpha ,\pi ,\eta } \right\},\left\{ {\alpha ,\pi ,\gamma } \right\},\left\{ {\alpha ,\pi ,\sigma } \right\},\left\{ {\alpha ,\pi ,\omega } \right\}\left\{ {\alpha ,\pi ,\tau } \right\}\) .
Vậy có \(8\) tập hợp thỏa mãn bài toán.
Tìm $m$ để \(\left[ { - 1;1} \right] \cap \left[ {m - 1;m + 3} \right] \ne \emptyset \)
+) TH1: \( - 1 \le m - 1 \le 1 \Leftrightarrow 0 \le m \le 2\)
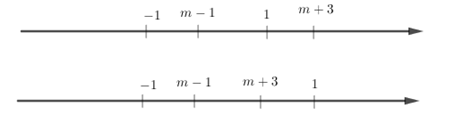
+) TH2: \(m - 1 \le - 1 \le m + 3 \Leftrightarrow \left\{ \begin{array}{l}m \le 0\\m \ge - 4\end{array} \right. \Leftrightarrow - 4 \le m \le 0\)
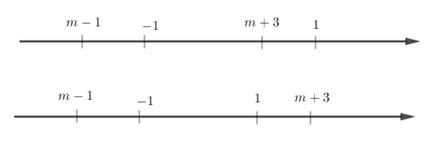
Kết hợp hai trường hợp trên ta được \(\left[ \begin{array}{l} 0 \le m \le 2\\ - 4 \le m \le 0\end{array} \right. \Leftrightarrow - 4 \le m \le 2\)
Cho tập hợp \(A = \left\{ {x \in R|{x^2} + 3x + 4 = 0} \right\}\), kết luận nào sau đây là đúng?
Ta có: \({x^2} + 3x + 4 = 0\) có \(\Delta = {3^2} - 4.4 = - 7 < 0\) nên phương trình vô nghiệm.
Vậy $A = \emptyset $.
Giá trị của $a$ mà \(\left[ {a;\dfrac{{a + 1}}{2}} \right] \subset \left(( - \infty ; - 1) \cup (1; + \infty )\right)\) là
Đặt \(B = \left( { - \infty ; - 1} \right),C = \left( {1; + \infty } \right),A = \left[ {a;\dfrac{{a + 1}}{2}} \right]\). Khi đó:
\(A \subset \left( {B \cup C} \right) \Leftrightarrow \left[ \begin{array}{l}\left[ {a;\dfrac{{a + 1}}{2}} \right] \subset \left( { - \infty ; - 1} \right)\\\left[ {a;\dfrac{{a + 1}}{2}} \right] \subset \left( {1; + \infty } \right)\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}a \le \dfrac{{a + 1}}{2} < - 1\\1 < a \le \dfrac{{a + 1}}{2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2a \le a + 1 < - 2\\2 < 2a \le a + 1\end{array} \right. \Leftrightarrow a < - 3\)
Cho hai tập hợp \(A = \left\{ {1;2;3} \right\}\) và \(B = \left\{ {1;2;3;4;5} \right\}.\) Có tất cả bao nhiêu tập \(X\) thỏa \(A \subset X \subset B?\)
Ta có \(A \subset X\) nên \(X\) có ít nhất \(3\) phần tử \(\left\{ {1;2;3} \right\}.\)
Ta có \(X \subset B\) nên \(X\) phải \(X\) có nhiều nhất \(5\) phần tử và các phần tử thuộc \(X\) cũng thuộc \(B.\)
Do đó các tập \(X\) thỏa mãn là \(\left\{ {1;2;3} \right\},\left\{ {1;2;3;4} \right\},\left\{ {1;2;3;5} \right\},\left\{ {1;2;3;4;5} \right\}\) \( \Rightarrow \) có \(4\) tập thỏa mãn.

