Đề thi giữa học kì 1 Toán lớp 8 trường THCS Nghĩa Tân

415 lượt xem

Bài trước

Bài sau

PHÒNG GD-ĐT CẦU GIẤY

TRƯỜNG THCS NGHĨA TÂN

Năm học 2016 - 2017

ĐỀ KIỂM TRA CHẤT LƯỢNG GIỮA HỌC KỲ I

MÔN TOÁN - LỚP 8

Thời gian: 90 phút

Bài 1 (2 điểm). Phân tích các đa thức thành nhân tử:

a) $3 x^{2} - 12 x + 12$ b) $x^{2} + 7 x + 7 y - y^{2}$

c) $x^{2} - x y - 6 y^{2}$ d) $x^{3} - 3 x^{2} - 6 x + 8$

a. $3 x^{2} - 12 x + 12 = 3 x^{2} - 6 x - 6 x + 12 = 3 x (x - 2) - 6 (x - 2) = (3 x - 6) (x - 2)$

b. $x^{2} + 7 x + 7 y - y^{2}$ $= (x^{2} - y^{2}) + 7 (x + y) = (x - y) (x + y) + 7 (x + y) = (x + y) (x - y + 7)$

c. $x^{2} - x y - 6 y^{2}$ $= x^{2} - 3 x y + 2 x y - 6 y^{2} = x (x - 3 y) + 2 y (x - 3 y) = (x + 2 y) (x - 3 y)$

d. $x^{3} - 3 x^{2} - 6 x + 8 = x^{3} - x^{2} - 2 x^{2} + 2 x - 8 x + 8$

$\begin{array}{l} = x^{2} (x - 1) - 2 x (x - 1) - 8 (x - 1) \\ = (x^{2} - 2 x + 8) (x - 1) \\ = (x^{2} - 4 x + 2 x + 8) (x - 1) \\ = (x - 4) (x + 2) (x - 1) \end{array}$

Bài 2 (2 điểm). Rút gọn rồi tính giá trị của mỗi biểu thức sau:

a) $A = {(7 x + 5)}^{2} + {(3 x - 5)}^{2} - (10 - 6 x) (5 + 7 x)$ tại $x = - 2$

$\begin{array}{l} A = {(7 x + 5)}^{2} + {(3 x - 5)}^{2} - (10 - 6 x) (5 + 7 x) \\ = {(7 x + 5)}^{2} + {(3 x - 5)}^{2} + 2 (3 x - 5) (5 + 7 x) \\ = {(7 x + 5 + 3 x - 5)}^{2} \\ = 100 x^{2} \end{array}$

Thay $x = - 2$ vào A ta được $A = 100 . {(- 2)}^{2} = 400$ .

b) $B = (2 x + y) (y^{2} + 4 x^{2} - 2 x y) - 8 x (x - 1) (x + 1)$ tại $x = - 2; y = 3$

$B = (2 x + y) (y^{2} + 4 x^{2} - 2 x y) - 8 x (x - 1) (x + 1)$ $= 8 x^{3} + y^{3} - 8 x^{3} + 8 x = y^{3} + 8 x$

Thay $x = - 2; y = 3$ vào B ta được $B = 3^{3} - 8.2 = 11$

Bài 3 (2 điểm). Tìm x, y, biết:

a) $x^{2} + 4 x = 0$

$\begin{array}{l} x^{2} + 4 x = 0 \\ x (x + 4) = 0 \\ \Rightarrow [\begin{array}{l} x = 0 \\ x + 4 = 0 \end{array} \\ \Rightarrow [\begin{array}{l} x = 0 \\ x = - 4 \end{array} \end{array}$

Vậy $x \in \{- 4; 0\}$ .

$\begin{array}{l} 5 x (3 x - 2) = 4 - 9 x^{2} \\ 5 x (3 x - 2) = (2 - 3 x) (2 + 3 x) \\ 5 x (3 x - 2) - (2 - 3 x) (2 + 3 x) = 0 \\ 5 x (3 x - 2) + (3 x - 2) (2 + 3 x) = 0 \\ (3 x - 2) (5 x + 2 + 5 x) = 0 \\ (3 x - 2) (8 x + 2) = 0 \\ \Rightarrow [\begin{array}{l} 3 x - 2 = 0 \\ 8 x + 2 = 0 \end{array} \\ \Rightarrow [\begin{array}{l} x = \frac{2}{3} \\ x = \frac{- 1}{4} \end{array} \end{array}$

Vậy $x \in \{\frac{- 1}{4}; \frac{2}{3}\}$ .

c) $x^{2} + 7 x = 8$

$\begin{array}{l} x^{2} + 7 x = 8 \\ x^{2} + 7 x - 8 = 0 \\ x^{2} + 8 x - x - 8 = 0 \\ x (x + 8) - (x + 8) = 0 \\ (x - 1) (x + 8) = 0 \\ \Rightarrow [\begin{array}{l} x - 1 = 0 \\ x + 8 = 0 \end{array} \\ \Rightarrow [\begin{array}{l} x = 1 \\ x = - 8 \end{array} \end{array}$

Vậy $x \in \{- 8; 1\}$ .

d) $2 x^{2} + 4 y^{2} + 10 x + 4 x y = - 25$

$\begin{array}{l} 2 x^{2} + 4 y^{2} + 10 x + 4 x y = - 25 \\ 2 x^{2} + 4 y^{2} + 10 x + 4 x y + 25 = 0 \\ (x^{2} + 10 x + 25) + (x^{2} + 4 x y + 4 y^{2}) = 0 \\ {(x + 5)}^{2} + {(x + 2 y)}^{2} = 0 \end{array}$

Vì ${(x + 5)}^{2} \geq 0$ và ${(x + 2 y)}^{2} \geq 0$ với mọi $x, y$ nên ${(x + 5)}^{2} + {(x + 2 y)}^{2} \geq 0$ với mọi $x, y$ .

Dấu “=” xảy ra khi và chỉ khi $\{\begin{cases} x + 5 = 0 \\ x + 2 y = 0 \end{cases} \Rightarrow \{\begin{cases} x = - 5 \\ y = \frac{5}{2} \end{cases}$ .

Vậy $(x; y) = (- 5; \frac{5}{2})$ .

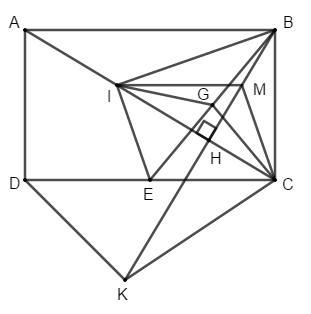
Bài 4 (3,5 điểm). Cho hình chữ nhật ABCD. Kẻ $B H ⊥ A C (H \in A C)$ . Các điểm I, M, E lần lượt là trung điểm của AH, BH và CD.

a) Chứng minh tứ giác ABMI là hình thang.

b) Chứng minh tứ giác IMCE là hình bình hành.

c) Gọi G là trung điểm của BE. Chứng minh M là trực tâm của tam giác IBC từ đó chứng minh tam giác IGC là tam giác cân.

Ảnh đính kèm

a. Xét tam giác $A B H$ có M là trung điểm của BH (gt), I là trung điểm của AH (gt)

IM là đường trung bình của tam giác ABH

$I M / / A B$ ; $I M = \frac{A B}{2}$

Suy ra tứ giác ABMI là hình thang (dấu hiệu nhận biết)

b. Ta có $I M = \frac{A B}{2}$ ; $A B = C D$

$\Rightarrow I M = C E = \frac{C D}{2}$ lại có $I M / / A B / / C E$

IMCE là hình bình hành (dấu hiệu nhận biết).

$\Rightarrow I E / / C M$

c. Ta có $I M / / A B$ mà $A B ⊥ B C$

$\Rightarrow I M ⊥ B C$

Xét tam giác IBC có:

$\{\begin{cases} I M ⊥ B C \\ B H ⊥ I C \\ I M \cap B H = \{M\} \end{cases}$ $\Rightarrow M$ là trực tâm tam giác IBC.

$\Rightarrow C M ⊥ I B$ mà $C M / / I E$

$\Rightarrow I E ⊥ I B$ .

$\Rightarrow Δ I E B$ vuông tại I, IG là trung tuyến.

$\Rightarrow I G = \frac{B E}{2}$ .(1)

Tam giác CBE vuông tại C, có CG là trung tuyến.

$\Rightarrow C G = \frac{B E}{2}$ (2).

Từ (1) và (2) suy ra $I G = C G$

$\Rightarrow Δ C G I$ cân tại G.

Bài 5 (0,5 điểm). Tìm GTNN của biểu thức $A = \frac{2 x^{2} + 2 x + 1}{x^{2} + 2 x + 1}, x \neq 1$ .

Ta có

$A = \frac{2 x^{2} + 2 x + 1}{x^{2} + 2 x + 1} = \frac{x^{2}}{{(x + 1)}^{2}} + \frac{x^{2} + 2 x + 1}{{(x + 1)}^{2}} = {(\frac{x}{x + 1})}^{2} + 1 \geq 1 \forall x \neq 1$

Vậy giá trị nhỏ nhất của A là 1.

Dấu bằng sảy ra khi $\frac{x}{x + 1} = 0 \Rightarrow x = 0$ .

Xem thêm các chương trình khác:

Bài trước

Bài sau

Đề thi Toán lớp 8 chọn lọc, bám sát đề thi chính thức

Đề thi giữa học kì 1 Toán lớp 8 trường THCS Nghĩa Tân

Xem thêm các chương trình khác: