Đề thi giữa học kì 1 Toán lớp 8 trường THCS Cao Viên

I.Phần trắc nghiệm ( 2 điểm )

Hãy chọn  chữ cái đứng trước câu trả lời đúng:

Câu 1: Kết quả phép tính $\left(4--3x\right).\left(-2x\right)$là:

A. 4 + 6x                        

B. 4 – 6x²                     

C. 8 – 6x                    

D. – 8x + 6x²

$\left(4--3x\right).\left(-2x\right)$$=-8\mathrm{x}+6{\mathrm{x}}^2$

Chọn D.

Câu 2 : Phân tích đa thức $9a^2-b^2$thành nhân tử là :

A. (3a – b)²                    

B. (3a –b )(3a + b)         

C. (b – 3a) (b + 3a)        

D. ( 9a + b) (9a – b)

$9a^2--b^2=\left(3\mathrm{a}+b\right)\left(3\mathrm{a}-b\right)$

Chọn B.

Câu 3:  $m^3-n^3$bằng:

A. (m - n)³

B. (m - n)(m² - mn + n²)

C. (m - n)(m² + mn + n²)

D. (m + n)(m² - mn + n²)

$m^3-n^3 =\left(m-n\right)\left(m^2+mn+n^2\right)$

Chọn C.

Câu 4 : Đa thức $3x^{2}y--4x{y}^3$chia hết cho đơn thức nào sau đây ?

A.x²y                             

B. xy³                             

C. x²y³                       

D. xy

$3x^{2}y--4x{y}^3=xy\left(3\mathrm{x}-4y^2\right)$.

Vậy $3x^{2}y--4x{y}^3$ chia hết cho $xy$

Chọn D.

Câu 5 : Tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường là:

A. Hình thang cân.             

B. Hình bình hành.

C. Hình chữ nhật.             

D. Hình thoi.

Chọn C.

Câu 6 :  Cho tam giác ABC có MN là đường trung bình (MN // AC) . Biết MN =  4cm .

Tính AC = ?

A. 2cm                         B. 4cm                             C. 8cm                       D. 16 cm

Vì MN là đường trung bình của tam giác ABC và AC = 2MN

Suy ra $AC = 2MN = 2.4cm = 8cm$

Chọn C.

Câu 7. Cho tam giác ABC vuông tại A có AM là trung tuyến, khi đó:

A. AM = AB.

B. AM = BC.

C. AM = AC.

D. AM = BM

Áp dụng định lý: Trong một tam giác vuông đường trung tuyến ứng với cạnh huyền bằng một phần hai cạnh huyền.

AM là trung tuyến của tam giác ABC vuông tại A nên $AM=MB=MC=\frac{BC}{2}$

Câu 8. Hình nào sau đây trục đối xứng?

A. Hình thang.

B. Hình thang vuông

C. Hình bình hành.

D. Hình chữ nhật.

Chọn D

II.Phần tự luận ( 8 điểm )

Bài 1: (1,5 điểm)Thực hiện các phép tính sau:

a) $\left(-4x^3{y}^3+x^3{y}^4\right):2x{y}^2--xy\left(2x--xy\right)$

b) $\left(x^2+1\right)\left(x--3\right)--\left(x--3\right)\left(x^2+3x+9\right)$

a. $\left(-4x^3{y}^3+x^3{y}^4\right):2x{y}^2--xy\left(2x--xy\right)$$=\left(-4+y\right)x^3{y}^3:2{\mathrm{xy}}^2-$$2{\mathrm{x}}^{2}y+x^2{y}^2$

$=-2x^{2}y+\frac{1}{2}{x}^2{y}^2-2{\mathrm{x}}^{2}y+x^2{y}^2=-4{\mathrm{x}}^{2}y+\frac{3}{2}{x}^2{y}^2$

b. $\left(x^2+1\right)\left(x--3\right)--\left(x--3\right)\left(x^2+3x+9\right)$$=\left(x-3\right)\left(x^2+1-x^2-3\mathrm{x}-9\right)=\left(x-3\right)\left(-3\mathrm{x}-8\right)$

$=-3{\mathrm{x}}^2+x+24$

Bài 2: (1,5 điểm) Phân tích các đa thức sau thành nhân tử

a) $5x^4-20x^2$

b) $x^2+14x+49--y^2$

c) $x^2 +9x+20$

a. $5x^4-20x^2$$=5x^2\left(x^2-4\right)=5{\mathrm{x}}^2\left(x-2\right)\left(x+2\right)$

b. $x^2+14x+49-y^2$$={\left(x+7\right)}^2-y^2=\left(x+y+7\right)\left(x-y+7\right)$

c.$\begin{array}{l}{x}^2 +9x+20=x^2+5\mathrm{x}+4\mathrm{x}+20\\ =x\left(x+5\right)+4\left(x+5\right)\\ =\left(x+4\right)\left(x+5\right)\\ \Rightarrow x^2 +9x+20=\left(x+4\right)\left(x+5\right)\end{array}$

Bài 3:(1,5 điểm)  Tìm x, biết:

a) $2x\left(3-x\right)+2x^2 =12$             

a) $2x\left(3-x\right)+2x^2 =12$                    

$6x-2{\mathrm{x}}^2+2{\mathrm{x}}^2=12$                    

$6\mathrm{x}=12$                                 

$x = 2$                               

Vậy $x = 2$.                                        

b)$x\left(x-2\right)- x+2 = 0$

$\mathrm{x}\left(x-2\right)-\left(x-2\right)=0$

 $\left(x-1\right)\left(x-2\right)=0$

$\Rightarrow \left[\begin{array}{l}x=1\\ x=2\end{array}\right.$

Vậy $x = 1$ hoặc $x = 2$.

Bài 4: (3 điểm)  Cho tam giác ABC vuông ở A. AM là đường trung tuyến. Kẻ MN $\perp$ AC (N$\in$AC ), MP $\perp$ AB (P$\in$AB).

a/ Chứng minh tứ giác APMN là hình chữ nhật

b/ Gọi E là điểm đối xứng của M qua N. Chứng minh tứ giác AECM là hình thoi.

c/ Gọi F là điểm đối xứng của M qua P. Chứng minh A là trung điểm của EF.

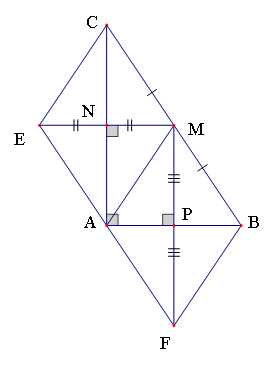
a. $MN\perp AC\Rightarrow \widehat{ANM}=90°$

$MP\perp AB\Rightarrow \widehat{APM}=90°$

Xét tứ giác APMN có $\hat{A}=\widehat{ANM}=\widehat{APM}=90°$

APMN là hình chữ nhật (dấu hiệu nhận biết).

b. E là điểm đối xứng của M qua N nên AC là đường trung trực của EM

 $\Rightarrow EM\perp AC;AM=A\mathrm{E}$.

$\Delta ABC$ vuông tại A, có AM là trung tuyến nên $AM = CM$ mà $AM=A\mathrm{E}$

$\Rightarrow A\mathrm{E}=CM$

Xét $\Delta AN\mathrm{E}$ và $\Delta CNM$ có:

$\widehat{ANE}=\widehat{CNM}=90°$

$AC=CM\left(cmt\right)$

$EN = MN$(gt)

$\Rightarrow \Delta AN\mathrm{E}=\Delta CNM$(cạnh huyền- cạnh góc vuông)

$\Rightarrow AN=CN$(2 cạnh tương ứng)

Xét tứ giác AMCE có $\left\{\begin{array}{l}EN=MN\left(gt\right)\\ AN=CN\left(cmt\right)\\ AC\cap EM=N\end{array}\right.$

Suy ra $A\mathrm{E}CM$ là hình bình hành (dấu hiệu nhận biết).

Mà $AC\perp EM\left(cmt\right)$

$\Rightarrow A\mathrm{E}CM$ là hình thoi. (dấu hiệu nhận biết)

$\Rightarrow A\mathrm{E}//CM$ hay $\mathrm{AE}//\mathrm{BC}$(1)

c. Chứng minh tương tự câu b ta có AMBF là hình thoi

$\Rightarrow AF//BM$ hay $\mathrm{AF}//BC$(2)

Từ (1) và (2) suy ra 2 điểm A, E, F thẳng hàng.

Mà $AE=AM;AF=AM$$\Rightarrow A\mathrm{E}=AF$

$\Rightarrow A$là trung điểm của đoạn thẳng $EF$

Bài 5: (0,5 điểm )

Xác định các hằng số a và b sao cho x⁴ + ax + b chia hết cho x² – 1

Để đa thức $f\left(x\right)=x^4+ax+b$ chia hết cho đa thức $f\left(x\right)=x^2-1$ thì $\left\{\begin{array}{l}f\left(1\right)=0\\ f\left(-1\right)=0\end{array}\right.$

Thay $x = 1$ vào đa thức $f\left(x\right)$ ta được: $f\left(1\right)=1^4+a+b$

$f\left(1\right)=0$; khi đó $a + b + 1 = 0$

Suy ra $a = - 1 - b$.

Thay $x = - 1$ vào đa thức $f\left(x\right)$ta được: $f\left(-1\right)=1-a+b$

$f\left(-1\right)=0$ khi đó $1 + b - a = 0$(2)

Thay $a = - 1 - b$ vào (2) ta được: $1 + b + 1 + b = 0$

$b = - 1$.

Với $b = - 1$ thì $a = - 1 - b = - 1 + 1 = 0$.

Vậy với $a = 0;b = - 1$ thì đa thức $f\left(x\right)=x^4+ax+b$ chia hết cho đa thức $x^2-1$.