Đề thi giữa học kì 1 Toán lớp 8 trường THCS An Sơn

Đề thi giữa học kì 1 môn Toán lớp 8 trường THCS An Sơn

Câu 1 (1,5 điểm): Làm tính nhân.

a) $2x.(x^2-3)$

b) $\left(5x--2y\right).(x^2--xy+1)$

c)$\left(x+1\right)\left(x--1\right)\left(x+2\right)$

a. $2x.(x^2-3) =2{\mathrm{x}}^3-6\mathrm{x}$

b. $\left(5x--2y\right).(x^2--xy+1) =5{\mathrm{x}}^3-5x^{2}y+5\mathrm{x}-2{\mathrm{x}}^{2}y+2\mathrm{x}{y}^2-2y$

$=5x^3-7{\mathrm{x}}^{2}y+2\mathrm{x}{y}^2-2y+5x$

c. $\left(x+1\right)\left(x--1\right)\left(x+2\right)$$=\left(x^2-1\right)\left(x+2\right)=x^3+2{\mathrm{x}}^2-x-2$

Câu 2 (2 điểm): Phân tích các đa thức sau thành nhân tử.

a) $2x-6y^2$            

b) $2x+2y-x^2 -xy$

c) $x^2-25+y^2+2xy$

d) $x^3 -9x^2 +7x+1$

a. $2x-6y^2$$=2\left(x-3y^2\right)$

b. $2x+2y-x^2 -xy$$=2\left(x+y\right)-x\left(x+y\right)=\left(2-x\right)\left(x+y\right)$

c. $x^2-25+y^2+2xy$$={\left(x+y\right)}^2-25=\left(x+y-5\right)\left(x+y+5\right)$

d. $x^3 -9x^2 +7x+1$$=x^3-x^2-8{\mathrm{x}}^2+8\mathrm{x}-x+1$

$\begin{array}{l}=x^2\left(x-1\right)-8\mathrm{x}\left(x-1\right)-\left(x-1\right)\\ =\left(x^2-8x-1\right)\left(x-1\right)\end{array}$

Câu 3 (1,5 điểm) Tìm x biết.

a) $x^2-2x+1=0$              

a. ‘$x^2-2x+1=0$           

${\left(x-1\right)}^2=0$                   

$x - 1 = 0$                           

$x = 1$                          

Vậy $x = 1$.         

b) $3x^3-48x=0$

 b. $3x^3-48x=0$

$3\mathrm{x}\left(x^2-16\right)=0$

$x\left(x-4\right)\left(x+4\right)=0$

$\Rightarrow \left[\begin{array}{l}x=0\\ x=4\\ x=-4\end{array}\right.$

                Vậy $x\in \left\{-4;0;4\right\}$.

Câu 4 (1 điểm) Rút gọn và tính giá trị biểu thức.

$A=\left(2x+3\right)(4x^2 -6x+9)-2(4x^3 -1)-2x$ với $x=2018$

$A=\left(2x+3\right)(4x^2 -6x+9)-2(4x^3 -1)-2x$$=8{\mathrm{x}}^3+27-8{\mathrm{x}}^3+2-2\mathrm{x}$

$=29-2\mathrm{x}$

Thay $x=2018$ vào A ta được $A = 29 - 2.2018 = - 4007$.

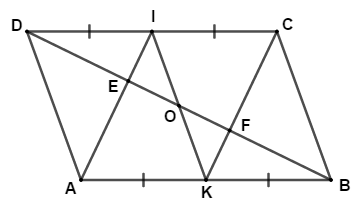
Câu 5 (3 điểm) Hình bình hành ABCD có ÐA= 110⁰. Gọi I, K lần lượt là trung điểm của CD, AB. Đường chéo BD cắt AI, CK lần lượt ở E,F.

a) Tính các góc của hình bình hành ABCD.

b) Chứng minh AI // CK và DE = EF = FB

c) Gọi O là trung điểm của BD, chứng minh I, O, K thẳng hàng.

a. $ABC\mathrm{D}$ là hình bình hành nên $\left\{\begin{array}{l}\hat{A}=\hat{C}=110°\\ \hat{B}=\hat{D}=180°-\hat{A}=180°-110°=70°\end{array}\right.$

b. ABCD là hình bình hành nên $AB//C\mathrm{D};AB=C\mathrm{D}$

$\Rightarrow CI//AK;\frac{C\mathrm{D}}{2}=\frac{AB}{2}$

$\Rightarrow CI//AK;CI=AK$

Tứ giác AKCI có $CI//AK;CI = AK$

$\Rightarrow AKCI$ là hình bình hành (dấu hiệu nhận biết)

$\Rightarrow AI//CK;CI=AK$(tính chất hình bình hành)

b. Xét tam giác DCF có $EI//CF$; I là trung điểm của CD.

$\Rightarrow EI$ là đường trung bình của tam giác ACF

$\Rightarrow E$là trung điểm của DF

$\Rightarrow DE=\mathrm{EF}$

Chứng minh tương tự ta có$KF$là đường trung bình của tam giác ABE.

$\Rightarrow \mathrm{EF}=\mathrm{BF}$

Suy ra $DE = EF = BF$.

c. Xét tam giác ABD có K là trung điểm của AB; O là trung điểm của BD.

$\Rightarrow KO$ là đường trung bình của tam giác ABD

$\Rightarrow KO//A\mathrm{D}$

Xét tam giác CBD có I là trung điểm của CD; O là trung điểm của BD.

$\Rightarrow OI$ là đường trung bình của tam giác CBD.

$\Rightarrow OI//CB$ mà  $CB//A\mathrm{D}$

$\Rightarrow OI//A\mathrm{D}$ mà $KO//A\mathrm{D}\left(cmt\right)$

Suy ra $O,I,K$ thẳng hàng.

Câu 6 (1 điểm) Chứng minh rằng nếu $a^3 +b^3 +c^3 =3abc$ và a,b,c là các số dương thì a = b = c.

Ta có

$a^3 +b^3 +c^3 =3abc$

$a^3 +b^3 +c^3 - 3abc=0$

$a^3+3{\mathrm{a}}^{2}b+3\mathrm{a}{b}^2+b^3+c^3-3\mathrm{a}b\left(a+b\right)-3\mathrm{a}bc=0$

$\begin{array}{l}{\left(a+b\right)}^3+c^3-3\mathrm{a}b\left(a+b+c\right)=0\\ \left(a+b+c\right)\left[{\left(a+b\right)}^2-ac-bc+c^2\right]-3\mathrm{a}b\left(a+b+c\right)=0\end{array}$

$\left(a+b+c\right)\left(a^2+2\mathrm{a}b+b^2-ac-bc+c^2-3\mathrm{a}b\right)=0$

$\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)=0$

Vì a, b, c là các số nguyên dương nên $a + b + c > 0$.

$\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)=0$ suy ra $a^2+b^2+c^2-ab-ac-bc=0$

$\Rightarrow 2\left(a^2+b^2+c^2-ab-ac-bc\right)=0$

$\begin{array}{l}{a}^2-2\mathrm{a}b+b^2+b^2-2bc+c^2+a^2-2\mathrm{a}c+c^2=0\\ {\left(a-b\right)}^2+{\left(b-c\right)}^2+{\left(a-c\right)}^2=0\end{array}$

$\Rightarrow \left\{\begin{array}{l}a-b=0\\ b-c=0\\ a-c=0\end{array}\right.$

Suy ra $a = b = c$.