Đề bài
Câu 1. Đốt cháy 3 lít hỗn hợp khí gồm hai hiđrocacbon no kế tiếp nhau trong dãy đồng đẳng, dẫn sản phẩm lần lượt qua bình (1) đựng CaCl2 khan rồi bình (2) đựng dung dịch KOH. Sau thí nghiệm khối lượng bình (1) tăng 6,43 gam, bình (2) tăng 9,82 gam. Xác định công thức hiđrocacbon và tính hàm lượng phần trăm (theo thể tích) của chúng trong hỗn hợp, các thể tích khí đo ở đktc.
Câu 2. Đốt cháy hoàn toàn 3,36 lít một ankan khí X (đktc), thu được 13,2 gam khí CO2. Xác định công thức phân tử của X.
Lời giải chi tiết
Câu 1.
+) Lập công thức hai hiđrocacbon no.
Gọi công thức của hiđrocacbon thứ nhất: \({C_n}{H_{2n + 2}}\) có (a mol)
và công thức của hiđrocacbon thứ hai: \({C_m}{H_{2m + 2}}\) có (b mol)
Ta có: nhỗn hợp \( = \dfrac{3}{{22,4}}\left( {mol} \right) \Rightarrow a + b = \dfrac{3}{{22,4}}\) (I)
Phản ứng:
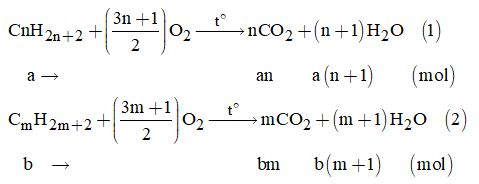
Vì bình (1) hấp thụ H2O nên khối lượng bình tăng bằng khối lượng H2O
\( \Rightarrow {m_{{H_2}O}} = 6,43\left( {gam} \right)\)
\(\Rightarrow {m_{{H_2}O}} = a\left( {n + 1} \right) + b\left( {m + 1} \right) \)\(\,= \dfrac{{6,43}}{{18}}{\rm{ }}\left( {II} \right)\)
Bình (2) hấp thụ CO2 nên khối lượng bình tăng bằng khối lượng CO2
\( \Rightarrow {m_{C{O_2}}} = 9,82gam \)\(\Rightarrow {n_{C{O_2}}} = an + bm = \dfrac{{9,82}}{{44}}{\rm{ }}\left( {III} \right)\)
Vì hai ankan kế tiếp nhau nên m = n + 1 (IV)
Từ (4) \( \Rightarrow an + b\left( {n + 1} \right) = \dfrac{{9,82}}{{44}}\)
\( \Leftrightarrow n\left( {a + b} \right) + b = \dfrac{{9,82}}{{44}}\)
\(\Leftrightarrow \dfrac{3}{{22,4}}.n + b = \dfrac{{9,82}}{{44}}\)
Vì là chất khí nên \(1 \le n \le 4\)
- Khi \(n = 1\) \( \Rightarrow b = \dfrac{{9,82}}{{44}} - \dfrac{3}{{22,4}} = \dfrac{{87,968}}{{985,6}} \)\(\,= 0,0893\left( {mol} \right)\)
Mà \(a + b = 0,134 \Rightarrow a = 0,0447\left( {mol} \right)\)
- Khi \(n = 2 \) \(\Rightarrow b = \dfrac{{9,82}}{{44}} - \dfrac{6}{{22,4}} = \dfrac{{ - 44,032}}{{985,6}} < 0\) (loại)
Do vậy khi n càng lớn thì b càng giảm nên loại các trường hợp còn lại.
Vậy nghiệm duy nhất: n = 1; m = n + 1 = 2
Suy ra công thức hai ankan: CH4 và C2H6
+) Tính thành phần phần trăm thể tích các khí:
Gọi a là số mol CH4 và b là số mol của C2H6 trong 3 lít hỗn hợp.
Ta có:
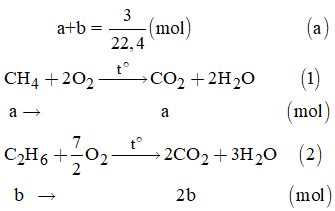
Từ (1) và (2) \( \Rightarrow a + 2b = \dfrac{{9,82}}{{44}}{\rm{ }}\left( b \right)\)
Giải (a) và (b), ta được: \(\left\{ \begin{array}{l}a = 0,0447\left( {mol} \right)\\b = 0,0893\left( {mol} \right)\end{array} \right.\)
Vì là chất khí nên %V = %n
Vậy: \(\% {V_{C{H_4}}} = \% {n_{C{H_4}}} \)\(\,= \dfrac{{0,0447}}{{0,0447 + 0,0893}} \times 100\% = 33,3\% \)
\(\% {V_{{C_2}{H_6}}} = \% {n_{{C_2}{H_6}}}\)\(\, = 100\% - 33,3\% = 66,7\% \)
Câu 2.
Ta có: \({n_{ankan}} = \dfrac{{3,36}}{{22,4}} = 0,15\left( {mol} \right);\)
\({n_{C{O_2}}} = \dfrac{{13,2}}{{44}} = 0,3\left( {mol} \right)\)
Phản ứng: \(\begin{array}{l}Cn{H_{2n + 2}} + \left( {\frac{{3n + 1}}{2}} \right){O_2} \to nC{O_2} + \left( {n + 1} \right){H_2}O{\rm{ }}\left( 1 \right)\\{\rm{ 0,15 }} \to {\rm{ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, 0,15n }}\left( {mol} \right)\end{array}\)
Từ (1) \({n_{C{O_2}}} = 0,15n = 0,3 \Rightarrow n = 2\)
Vậy công thức phân tử: C2H6.

