Giải toán tư duy bằng phương pháp loại trừ, lựa chọn và chia trường hợp

Ta dùng phương pháp loại trừ. Điều kiện 2) loại các phương án A và D

Điều kiện giảng viên kinh nghiệm đi kèm giảng viên chưa kinh nghiệm loại các phương án B và E. Vậy chỉ còn phương án C

Xét các điều kiện:

(1) Mỗi bộ phận một tầng

(2) Mỗi tầng được bố trí tối đa 4 bộ phận

(3) P phải cùng tầng với T

(4) H phải được bố trí tầng liền trên I

(5) L phải chiếm toàn bộ 1 tầng

Đáp án A:

 => Không thỏa mãn (4)

=> Loại A.

Đáp án B:

=> Không thỏa mãn (3)

Đáp án C:

=> Thỏa mãn 5 điều kiện

Đáp án D:

=> Không thỏa mãn (4)

Theo câu 2 và câu 3 ta có: Chén đựng cà phê và cốc đựng nước chè

=> Vại lớn phải đựng sữa, và vại nhỏ đựng ca cao.

Còn lại chai đựng bia như bảng sau:

Ta dùng phương pháp loại trừ. Điều kiện 1) loại phương án C. Điều kiện 2) loại phương án A. Điều kiện 3) và 1) loại phương án D. Vậy chỉ còn phương án B

Theo câu 2 ta có: Chén đựng cà phê và ở chính giữa.

Khi đó, vật đựng chè là vại to hoặc cốc, và thứ tự của nó thay đổi sau khi chuyển chén, vậy vật đựng chè chỉ có thể là cốc.

Chiếc chén được chuyển vào giữa 2 vật đựng chè và đựng sữa, vậy vật đựng chè và vật đựng sữa chỉ có thể là chai và vại to hoặc vại to và cốc.

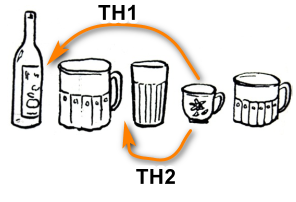
Ta xét 2 khả năng đó:

TH1: Chén được chuyển vào giữa chai và vại to: Ta thấy ngay vại to chỉ có thể đựng chè hoặc sữa. Nhưng thứ tự vại to trở nên ở giữa, nên nó đựng cà phê. Vậy khả năng này không thoả mãn. Suy ra chỉ là khả năng kia.

TH2: Chén được chuyển vào giữa vại to và cốc; vị trí của chén trở thành giữa. Vậy chén đựng cà phê.

Chiếc chén được chuyển vào giữa 2 vật đựng chè và đựng sữa, vậy vật đựng chè và vật đựng sữa chỉ có thể là chai và vại to hoặc vại to và cốc.

Nếu chén được chuyển vào giữa chai và vại to: Ta thấy ngay vại to chỉ có thể đựng chè hoặc sữa. Nhưng thứ tự vại to trở nên ở giữa, nên nó đựng cà phê.

Vậy khả năng này không thoả mãn. Suy ra chỉ là khả năng kia.

Vậy chén được chuyển vào giữa vại to và cốc.

Các đội hình:

c; a; d; b; f; e

c; a; d; f; b; e

e ngồi vị trí số 6

a ngồi giữa c và f; b và f luôn ngồi cạnh nhau; e không ngồi cạnh d

\( \Rightarrow \)e và d chỉ ngồi ở vị trí 1 và 6

e không ngồi cạnh d => loại D

b và f luôn ngồi cạnh nhau => loại C

c không ngồi ở vị trí thứ 3 => loại B

Chỉ có đáp án A thỏa mãn

Đạt làm nhóm trưởng thì Hoàng làm thành viên.

=> Nhóm luôn có Đạt, Vân, Hoàng rồi nên không thể có thêm người khác

=> Đáp án B, C, D đều thêm 1 người=>Loại.

Nếu Huệ là nhóm trưởng thì Duyên, Dương và Đức không thể tham gia. Còn lại Đạt, Hoàng và Vân nhưng chỉ có duy nhất 1 nhóm trưởng và Đạt hoặc Hoàng chỉ có thể được nhận vào dự án nếu 1 trong 2 làm nhóm trưởng nên Huệ không thể làm nhóm trưởng

Nếu Huệ là Thành viên trong dự án thì Duyên và Dương không thể => loại B,A

Nếu Đức là thành viên trong dự án thì Dương cũng như thế=> loại D

Đạt hoặc Hoàng chỉ có thể được nhận vào dự án nếu 1 trong 2 làm nhóm trưởng => Loại D

Nếu Đức là thành viên trong Dự án thì Dương cũng như thế => Loại C,A

Nếu C, A, I đôi một khác nhóm và I cùng nhóm với G ta có 2 cách xếp

(D A B); (E I G); (C H F) và (D I G); (E A B); (C F H)

A và B cùng nhóm nên thành viên còn lại chỉ có thể là H hoặc I