Giải toán tư duy bằng phương pháp lập bảng
Kỳ thi ĐGNL ĐHQG Hồ Chí Minh
Nếu đúng là có 1 xe ở giữa xe chở S và xe U lái thì xe nào dưới đây chở Y
Ta có:

Xe U lái thì chỉ có thể là xe 1 và xe 2
=> Xe chở S không thể là xe 1 và 2 được
=> Xe chở S chỉ có thể là xe 4, vì xe 3 đã có X và Z
=> Xe U lái là xe 2
=> Xe 5 chở Y vì Y là nam.

Nếu S và V trên 2 xe kề nhau thì tài xế nào dưới đây chắc chắn không chở nhà ngoại giao nào.

Nếu S và V trên 2 xe kề nhau thì U chở S
Khi đó nhà ngoại giao cuối cùng là nam nên không thể ở trên xe V
=> V chắc chắn không chở ai
Nếu S ở xe 5 thì câu nào dưới đây có thể sai.

Vì Y là nam nên Y chỉ có thể đi xe 4
=> T và Y đi cùng xe=> A đúng.
Đáp án V=C: U và V đi xe 1 hoặc xe 2=> Đáp án C đúng
Đáp án D có thể sai vì: V có thể ở xe 1 và X có thể ở xe 2
Câu nào dưới đây là đầy đủ và chính xác danh sách các xe có thể có nữ
Từ đề bài ta có:

Vì Z là nam nên Z chỉ có thể ngồi xe 3,4,5.
Mà còn 2 xe đằng sau xe chở Z là xe có tài xế T và W
=> Z ở xe đi thứ 3
=> T lái xe 4
Hai xe đầu không có nam
=>Tài xế đều là nữ
=>Tài xế của 2 chiếc xe đầu là U,V
=> Các xe chắc chắn có nữ là 1,2,4.
Nếu thành viết số 54, những số của ai được xác định?
Số của Thành là 54 mà số của Hoàng nhỏ hơn số của Thành nên số của Hoàng chỉ có thể là 32 hoặc 12.
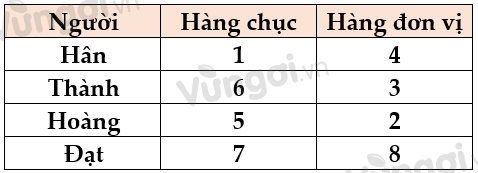
Nếu Hoàng viết số 32 thì còn lại các chữ số 1; 6; 7; 8
Thì Đạt sẽ có hàng chục cao hơn hàng chục của Hân nên ta hoàn toàn có thể xác định được số của Đạt và Hân.
Vì chữ số 3 ở hàng chục rồi nên chữ số 6 không thể ở hàng chục được => Chữ số 6 ở hàng đơn vị.
\( \Rightarrow \) Có thể xác định được số của tất cả mọi người, chẳng hạn:
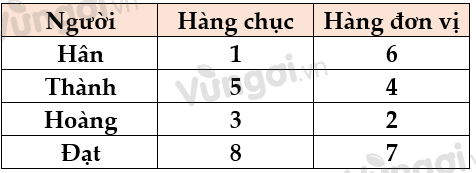
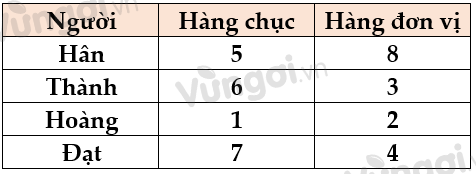
Nếu Hoàng viết số 12 thì còn lại các chữ số 3; 6; 7; 8
Thì Đạt sẽ có hàng chục cao hơn hàng chục của Hân nên ta hoàn toàn có thể xác định được số của Đạt và Hân.
\( \Rightarrow \) Có thể xác định được số của tất cả mọi người, chẳng hạn:
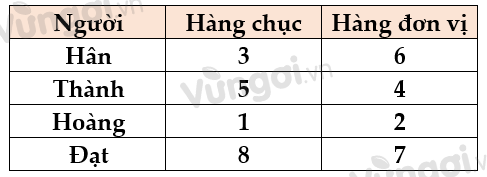
Nếu số của Hân nhỏ hơn số của Hoàng, điều nào sau đây chắc chắn sai?
Số của Đạt lớn nhất và số của Thành lớn hơn số của Hoàng nên ta có: Đạt>Thành>Hoàng. Mà số của Hân nhỏ hơn số của Hoàng
=>Ta có thứ hạng giảm dần của các số được viết: Đạt – Thành – Hoàng – Hân.
Xét A: Hân viết số tận cùng là 4.
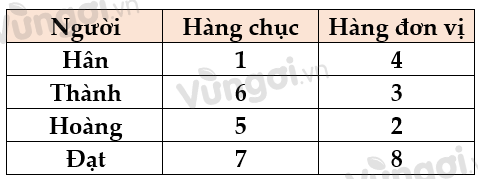
Xét B: Nếu Hân có chữ số tận cùng là 3 thì chữ số hàng chục là 6 nên số của Hân chỉ nhỏ hơn tối đa là 2 số, mâu thuẫn với điều kiện số của Hân nhỏ hơn 3 số của 3 người còn lại.
Xét C: Đạt viết số tận cùng là 4.
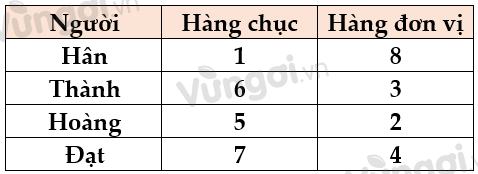
Xét D: Đạt viết số tận cùng là 8.
\( \Rightarrow \) Chọn B
Đâu có thể là các số 4 bạn đã viết?
Số cuối của Hoàng là chữ số 2 nên Loại A và C.
Số hàng chục là số 6 thì số hàng đơn vị là số 3 nên phải có số 63 nên loại B.
Đạt: 74; Hân: 58; Thành: 63; Hoàng: 12
Điều nào sau đây có thể đúng?
- Thành viết hàng chục là 8 thì Thành là người viết số lớn nhất (mâu thuẫn với số của Đạt viết lớn nhất) nên Loại B.
- Thành viết hàng chục là 1 thì Thành là người viết số bé nhất (mâu thuẫn với số của Thành lớn hơn số của Hoàng ) nên Loại C.
- Đạt có chữ số hàng chục là 4 mà Đạt là số lớn nhất thì các số 3, 2, 1 là các số ở hàng chục 3 người còn lại viết, mà điều kiện là số cuối của Hoàng là số 2 nên Loại D
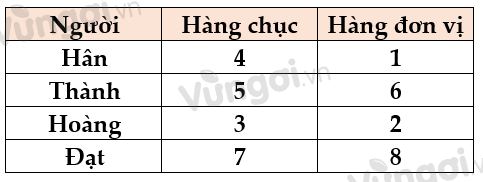
- Đáp án A: Hân viết số có hàng chục là 4 mà Hoàng viết số có chữ số tận cùng là 2. Khi đó 2 số chẵn còn lại chỉ có chữ số hàng đơn vị là 6 và 8. Ta có thể điền vào bảng các số thỏa mãn đề bài như sau:
Chỉ sử dụng xe buýt, hành khách KHÔNG THỂ đi bằng phương tiện giao thông công cộng từ:
Ta có bảng:

Xe điện ngầm: \(T \Rightarrow R \Rightarrow S \Rightarrow G \Rightarrow H \Rightarrow I\)
Xe buýt: \(R \Rightarrow {\rm{W}} \Rightarrow L \Rightarrow G \Rightarrow F\)
Xe buýt nhanh: \(R \Rightarrow L \Rightarrow F\)
Vậy:
+) Đáp án A đúng vì hành khách đi xe buýt từ \(F \Rightarrow G \Rightarrow L \Rightarrow {\rm{W}} \Rightarrow R\)
+) Đáp án B đúng vì hành khách đi xe buýt thường từ \(G \Rightarrow L\) rồi đổi tuyến qua xe buýt nhanh ở L rồi đi tiếp đến R
+) Đáp án C sai vì chỉ có xe điện ngầm dừng lại ở bến H
+) Đáp án D đúng vì hành khách đi xe buýt từ \(L \Rightarrow {\rm{W}} \Rightarrow R\)
Nếu một vụ cháy làm đóng cửa đoạn đường điện ngầm ở R, nhưng xe điện ngầm vẫn chạy được được từ I đến S và xe buýt thường vẫn dừng lại ở R, một hành khách bất kì KHÔNG THỂ đi bằng phương tiện giao thông công cộng đến?

Xe điện ngầm: \(T \Rightarrow R \Rightarrow S \Rightarrow G \Rightarrow H \Rightarrow I\)
Xe buýt: \(R \Rightarrow {\rm{W}} \Rightarrow L \Rightarrow G \Rightarrow F\)
Xe buýt nhanh: \(R \Rightarrow L \Rightarrow F\)
Vậy nếu đóng cửa đoạn đường điện ngầm ở R thì hành khách không thể đến T vì chỉ có xe điện ngầm đi từ R đến T và R lại đóng cửa
Để di chuyển bằng phương tiện giao thông công cộng từ S đến I, hành khách phải đi qua các bến nào sau đây
Ta có bảng

Xe điện ngầm: \(T \Rightarrow R \Rightarrow S \Rightarrow G \Rightarrow H \Rightarrow I\)
Xe buýt: \(R \Rightarrow {\rm{W}} \Rightarrow L \Rightarrow G \Rightarrow F\)
Xe buýt nhanh: \(R \Rightarrow L \Rightarrow F\)
Do chỉ có xe điện ngầm đi được đến bến I nên chắc chắn khi đi từ S đến I hành khách phải đi qua hai bến G và H
Nếu tất cả xe buýt thường sẽ không chạy trong giờ cao điểm do bị lỗi kỹ thuật, có thể một hành khách nào đó lên xe buýt nhanh tại L và sau đó đi đến G?
Ta có bảng:

Xe điện ngầm: \(T \Rightarrow R \Rightarrow S \Rightarrow G \Rightarrow H \Rightarrow I\)
Xe buýt: \(R \Rightarrow {\rm{W}} \Rightarrow L \Rightarrow G \Rightarrow F\)
Xe buýt nhanh: \(R \Rightarrow L \Rightarrow F\)
Để đến G, hành khách phải đến R sau đó đi tàu điện ngầm đến G.
Trong một bảng đấu loại bóng đá có 4 đội A, B, C, D. Người ta đưa ra 3 dự đoán :
a/ Đội A nhì, đội B nhất.
b/ Đội B nhì, đội D ba.
c/ Đội C nhì, đội D tư.
Kết quả dự đoán đều có một ý đúng, một ý sai. Hãy xác định thứ tự của mỗi đội.
Ta ghi ba dự đoán vào ba dòng trong bảng sau :
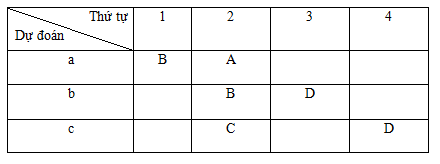
Vì có nhiều dự đoán đề cập đến đội về nhì nên ta xét đội nào về nhì.
Giả sử đội A về nhì là đúng thì các đội B và C về nhì là sai, do đó D về thứ ba (theo b) và về thứ tự (theo c) , vô lí.
Vậy đội A về nhì là sai, do đó theo a thì đội B về nhất. Đội B về nhì là sai nên theo b thì đội D về thứ 3. Đội D về thứ tư là sai nên theo c thì đội C về thứ nhì. Còn lại đội A về thứ tư.
Trong một cuộc đua xe đạp, 4 VĐV An, Bình, Cường, Dũng đã đạt bốn giải đầu tiên.
Trong các câu sau đây, mỗi câu chỉ đúng về một VĐV:
a) Bình giải nhất, Dũng giải nhì.
b) Bình giải nhì, Cường giải ba.
c) An giải nhì, Cường giải tư.
Hãy xác định giải của từng VĐV theo thứ tự: Nhất, Nhì, Ba, Tư?
Dựa vào dữ liệu đề bài ta có bảng
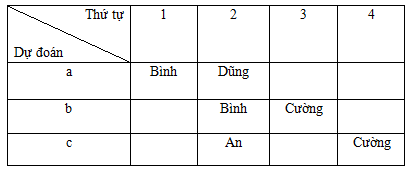
Giả sử Bình giải nhất đúng thì Dũng giải nhì và Bình giải nhì là sai => Cường giải ba là đúng (theo b) => Cường giải tư là sai=> An giải Nhì là đúng (theo c). Còn lại Dũng giải tư.
Vậy Bình giải nhất, An giải nhì, Cường giải ba, Dũng giải tư.
Trong 1 buổi học nữ công ba bạn Cúc, Đào, Hồng làm 3 bông hoa cúc, đào, hồng. Bạn làm hoa hồng nói với Cúc : Thế là trong chúng ta chẳng ai làm loại hoa trùng với tên mình cả! Hỏi ba bạn Cúc, Đào, Hồng đã làm lần lượt những hoa nào?
Ta có bảng sau:
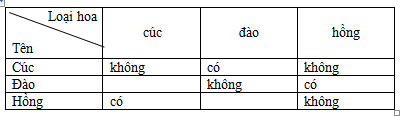
Dựa vào bảng ta thấy: Cúc làm hoa đào
Đào làm hoa hồng
Hồng làm hoa cúc.
Ba người thợ hàn, thợ tiện, thợ điện đang ngồi trò chuyện trong giờ giải lao. Người thợ hàn nhận xét :
Ba ta làm nghề trùng với tên của 3 chúng ta nhưng không ai làm nghề trùng với tên của mình cả.
Bác Điện hưởng ứng : Bác nói đúng.
Hãy cho biết nghề nghiệp của các bác Điện, Hàn, Tiện?
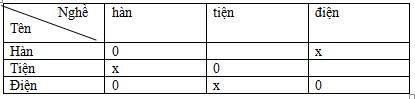
Vì bác thợ hàn nhận xét và bác Điện hưởng ứng nên bác thợ hàn không tên là Điện.
Đồng thời bác thợ hàn nói: “Ba chúng ta làm nghề trùng với tên của 3 chúng ta nhưng không ai làm nghề trùng với tên của mình cả”, nghĩa là bác thợ hàn cũng không tên là Hàn.
Do đó bác thợ hàn tên là Tiện.
Lại có bác Điện không làm thợ điện cũng không làm thợ hàn (vì bác Tiện đã làm thợ hàn) nên bác Điện làm thợ tiện.
Còn lại bác Hàn làm thợ điện.
Vậy: Bác Điện làm thợ tiện, bác Hàn phải làm thợ điện, bác Tiện phải làm thợ hàn.
Năm người thợ tên là : Da, Điện, Hàn, Tiện và Sơn làm 5 nghề khác nhau trùng với tên của tên của 5 người đó nhưng không có ai tên trùng với nghề của mình. Tên của bác thợ da trùng với nghề của anh vợ mình và vợ bác chỉ có 2 anh em. Bác Tiện không làm thợ sơn mà lại là em rể của bác thợ hàn. Bác thợ sơn và bác Da là 2 anh em cùng họ. Cho biết bác Da và bác Tiện làm nghề gì?
Ta có bảng sau:
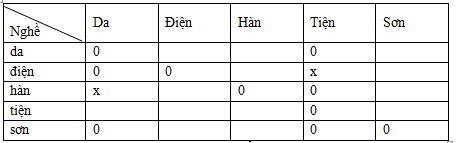
- Bác Tiện không làm thợ sơn. Bác Tiện là em rể của bác thợ hàn nên bác Tiện không làm thợ hàn
=>Bác Tiện chỉ có thể là thợ da hoặc thợ điện.
- Nếu bác Tiện làm thợ da thì bác Tiện là em rể của thợ hàn.
Mà tên của bác Tiện trùng với nghề của anh vợ mình=> Bác Tiện là em rể của thợ tiện.
Như vậy bác Tiện vừa là em rể của bác thợ tiện vừa là em rể của bác thợ hàn mà vợ bác Tiện chỉ có 2 anh em. Điều này vô lí.
=> Bác Tiện là thợ điện
- Bác Da và bác thợ sơn là 2 anh em cùng họ nên bác Da không phải là thợ sơn. Theo lập luận trên bác Da không là thợ tiện => Bác Da là thợ hàn.
Trên bàn là 3 cuốn sách giáo khoa : Văn, Toán và Địa lí được bọc 3 màu khác nhau: Xanh, đỏ, vàng. Cho biết cuốn bọc bìa màu đỏ đặt giữa 2 cuốn Văn và Địa lí, cuốn Địa lí và cuốn màu xanh mua cùng 1 ngày. Bạn hãy xác định màu bìa các cuốn sách Văn, Toán, Địa?
Ta có bảng sau:
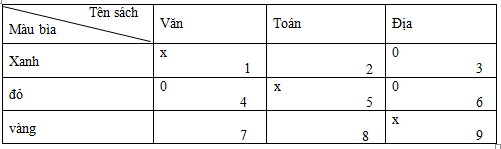
Theo đề bài “Cuốn bìa màu đỏ đặt giữa 2 cuốn Văn và Địa lí” . Vậy cuốn sách Văn và Địa lí đều không đặt màu đỏ cho nên cuốn toán phải bọc màu đỏ. Ta ghi số 0 vào ô 4 và 6, đánh dấu x vào ô 5.
Mặt khác, “Cuốn Địa lí và cuốn màu xanh mua cùng ngày”. Điều đó có nghĩa rằng cuốn Địa lí không bọc màu xanh. Ta ghi số 0 vào ô 3.
- Nhìn vào cột thứ 4 ta thấy cuốn địa lí không bọc màu xanh, cũng không bọc màu đỏ. Vậy cuốn Địa lí bọc màu vàng. Ta đánh dấu x vào ô 9.
- Nhìn vào cột 2 và ô 9 ta thấy cuốn Văn không bọc màu đỏ, cũng không bọc màu vàng. Vậy cuốn Văn bọc màu xanh. Ta đánh dấu x vào ô 1.
Kết luận: Cuốn Văn bọc màu xanh, cuốn Toán bọc màu đỏ, cuốn Địa lí bọc màu vàng.
Giờ Văn cô giáo trả bài kiểm tra. Bốn bạn Tuấn, Hùng, Lan, Quân ngồi cùng bàn đều đạt điểm 8 trở lên. Giờ ra chơi Phương hỏi điểm của 4 bạn, Tuấn trả lời :
- Lan không đạt điểm 10, mình và Quân không đạt điểm 9 còn Hùng không đạt điểm 8.
Hùng thì nói :
- Mình không đạt điểm 10, Lan không đạt điểm 9 còn Tuấn và Quân đều không đạt điểm 8.
Bạn hãy cho biết Tuấn, Hùng, Lan, Quân lần lượt được mấy điểm?
Từ các dữ kiện đề bài cho ta có bảng:
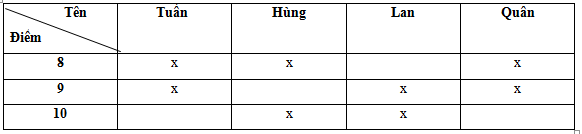
Từ bảng suy ra Tuấn đạt điểm 10, Hùng đạt điểm 9, Lan đạt điểm 8, Quân đạt điểm 10.
Trong 1 cuộc chạy thi 4 bạn Anh, Bình, Cường, Dũng đạt 4 giải : nhất, nhì, ba, tư. Khi được hỏi : Bạn Dũng đạt giải mấy thì 4 bạn trả lời :
Anh : Tôi nhì, Bình nhất.
Bình : Tôi cũng nhì, Dũng ba.
Cường : Tôi mới nhì, Dũng tư.
Dũng : 3 bạn nói có 1 ý đúng 1 ý sai.
Em cho biết mỗi bạn: Anh, Bình, Cường, Dũng lần lượt đạt các giải nào?
Ta có bảng:
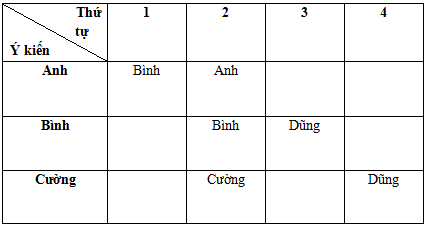
Giả sử Anh đạt giải nhì là đúng => Bình đạt giải nhất là sai, Bình và Cường đạt giải nhì cũng sai
=> Dũng đạt giải ba và giải tư là đúng (vô lý) => điều giả sử là sai
Suy ra Bình đạt giải nhất là đúng=> Anh đạt giải nhì, Bình đạt giải nhì là sai
=> Dũng đạt giải ba là đúng=> Dũng k thể đạt giải tư => Dũng đạt giải tư là sai
=> Cường đạt giải nhì đúng. Còn lại Anh đạt giải tư

