Bài toán tương giao đồ thị
Kỳ thi ĐGNL ĐHQG Hồ Chí Minh
Tọa độ giao điểm của đường thẳng $d:y = 3x$ và parabol $\left( P \right):y = 2{x^2} + 1$ là:
Phương trình hoành độ $2{x^2} + 1 = 3x$.
$ \Leftrightarrow 2{x^2} - 3x + 1 = 0 \Leftrightarrow \left[ \begin{gathered} x = 1 \Rightarrow y = 3 \hfill \\ x = \dfrac{1}{2} \Rightarrow y = \dfrac{3}{2} \hfill \\ \end{gathered} \right.$
Vậy có hai giao điểm là $\left( {1;3} \right)$ và $\left( {\dfrac{1}{2};\dfrac{3}{2}} \right)$.
Số giao điểm của đồ thị hàm số $y = {x^3} - 2{x^2} + x - 1$ và đường thẳng $y = 1 - 2x$ là:
Số giao điểm của hai đồ thị hàm số đã cho là số nghiệm của phương trình:
$\begin{gathered} {x^3} - 2{x^2} + x - 1 = 1 - 2x \Leftrightarrow {x^3} - 2{x^2} + 3x - 2 = 0 \hfill \\ \Leftrightarrow \left( {x - 1} \right)\left( {{x^2} - x + 2} \right) = 0 \Leftrightarrow x = 1 \hfill \\ \end{gathered} $
Vậy hai đồ thị hàm số đã cho có $1$ giao điểm duy nhất.
Cho hai đồ thị hàm số $y = {x^3} + 2{x^2} - x + 1$ và đồ thị hàm số $y = {x^2} - x + 3$ có tất cả bao nhiêu điểm chung?
Số giao điểm của hai đồ thị hàm số đã cho là số nghiệm của phương trình:
$\begin{gathered}{x^3} + 2{x^2} - x + 1 = {x^2} - x + 3 \Leftrightarrow {x^3} + {x^2} - 2 = 0 \hfill \\ \Leftrightarrow \left( {x - 1} \right)\left( {{x^2} + 2x + 2} \right) = 0 \Leftrightarrow x = 1 \hfill \\ \end{gathered} $
Như vậy hai đồ thị có $1 $ điểm chung.
Các đồ thị hàm số $y = {x^4} - 2{x^2} + 2$ và $y = - {x^2} + 4$ có tất cả bao nhiêu điểm chung?
Phương trình hoành độ giao điểm của hai đồ thị hàm số đã cho là:
$\begin{gathered}{x^4} - 2{x^2} + 2 = - {x^2} + 4 \Leftrightarrow {x^4} - {x^2} - 2 = 0 \hfill \\ \Leftrightarrow \left[ \begin{gathered} {x^2} = - 1 < 0(L) \hfill \\ {x^2} = 2 \hfill \\ \end{gathered} \right. \Leftrightarrow x = \pm \sqrt 2 \hfill \\ \end{gathered} $
Như vậy hai đồ thị có $2$ giao điểm.
Số giao điểm của hai đồ thị hàm số $y = 3{x^2}$ và $y = {x^3} + {x^2} + x + 1$ là:
Phương trình hoành độ giao điểm: $3{x^2} = {x^3} + {x^2} + x + 1 \Leftrightarrow {x^3} - 2{x^2} + x + 1 = 0$.
Xét hàm $f\left( x \right) = {x^3} - 2{x^2} + x + 1$ ta có:
$f'\left( x \right) = 3{x^2} - 4x + 1 = 0 \Leftrightarrow \left[ \begin{gathered} x = 1 \Rightarrow f\left( 1 \right) = 1 \hfill \\ x = \dfrac{1}{3} \Rightarrow f\left( {\dfrac{1}{3}} \right) = \dfrac{{31}}{{27}} \hfill \\ \end{gathered} \right.$
Bảng biến thiên:
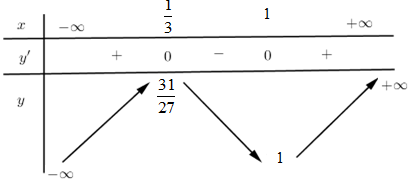
Từ bảng biến thiên ta thấy đường thẳng $y = 0$ chỉ cắt đồ thị hàm số tại $1$ điểm duy nhất nên hai đồ thị hàm số cắt nhau tại duy nhất $1$ điểm.
Tìm $m$ để phương trình ${x^5} + {x^3} - \sqrt {1 - x} + m = 0$ có nghiệm trên $\left( { - \infty ;1} \right]$.
Ta có số nghiệm của phương trình đã cho là số giao điểm của đồ thị (C): $y = {x^5} + {x^3} - \sqrt {1 - x} $ và đường thẳng d: $y = - m$.
Xét hàm số (C): $y = {x^5} + {x^3} - \sqrt {1 - x} $ có: $y' = 5{x^4} + 3{x^2} + \dfrac{1}{{2\sqrt {1 - x} }} > 0\,\,\forall x \in \left( { - \infty ;1} \right)$$ \Rightarrow $ hàm số luôn đồng biến trên $\left( { - \infty ;1} \right]$.
Lại có $y\left( 1 \right) = 2$.
Ta có BBT:
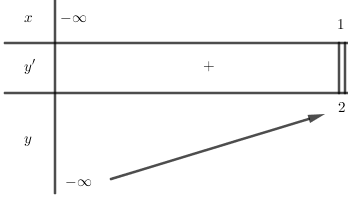
Theo BBT ta thấy pt có nghiệm $ \Leftrightarrow - m \leqslant 2 \Leftrightarrow m \geqslant - 2$.
Cho hàm số $y = {x^3} + 3{x^2} + m$ có đồ thị $\left( C \right)$.Để đồ thị $\left( C \right)$ cắt trục hoành tại ba điểm $A,B,C$ sao cho $C$ là trung điểm của $AB$ thì giá trị của tham số $m$ là:
Vì đồ thị của hàm đa thức bậc 3 luôn có tâm đối xứng $I\left( {{x_0};{y_0}} \right)$ có hoành độ ${x_0}$ là nghiệm của phương trình $y''\left( {{x_0}} \right) = 0$
Vậy đồ thị $\left( C \right)$ cắt trục hoành tại ba điểm $A, B, C$ sao cho $C$ là trung điểm $AB$
$ \Leftrightarrow $$C$ là tâm đối xứng của $\left( C \right)$
Ta có:
$y' = 3{x^2} + 6x \Rightarrow y'' = 6x + 6 = 0 \Leftrightarrow x = - 1 \Rightarrow y = m + 2 \Rightarrow C\left( { - 1;m + 2} \right)$$C \in Ox \Leftrightarrow y = 0 \Leftrightarrow m + 2 = 0 \Leftrightarrow m = - 2$
Biết đường thẳng $y = mx + 1$ cắt đồ thị hàm số $y = {x^3} - 3x + 1$ tại ba điểm phân biệt. Tất cả các giá trị thực của tham số $m$ là:
Xét phương trình hoành độ giao điểm $mx + 1 = {x^3} - 3x + 1$
$ \Leftrightarrow {x^3} - 3x - mx = 0 \Leftrightarrow x\left( {{x^2} - 3 - m} \right) = 0 \Leftrightarrow \left[ \begin{gathered} x = 0 \hfill \\ {x^2} = m + 3\left( * \right) \hfill \\ \end{gathered} \right.$
Để đường thẳng cắt đồ thị hàm số tại $3$ điểm phân biệt thì $\left( * \right)$ phải có hai nghiệm phân biệt khác $0$ $ \Leftrightarrow m + 3 > 0 \Leftrightarrow m > - 3$.
Cho hàm số $y = {x^3} - \left( {m + 3} \right){x^2} + \left( {2m - 1} \right)x + 3\left( {m + 1} \right)$. Tập hợp tất cả các giá trị của $m$ để đồ thị hàm số đã cho cắt trục hoành tại ba điểm phân biệt có hoành độ âm là:
Phương trình hoành độ giao điểm của đồ thị hàm số và trục hoành là:
${x^3} - \left( {m + 3} \right){x^2} + \left( {2m - 1} \right)x + 3\left( {m + 1} \right) = 0$
$ \Leftrightarrow \left( {x + 1} \right)\left[ {{x^2} - \left( {m + 4} \right)x + 3\left( {m + 1} \right)} \right] = 0 \Leftrightarrow \left[ \begin{gathered} x = - 1 \hfill \\{x^2} - \left( {m + 4} \right)x + 3\left( {m + 1} \right) = 0\left( * \right) \hfill \\ \end{gathered} \right. $
Để đồ thị hàm số cắt trục hoành tại $3$ điểm phân biệt có hoành độ âm thì phương trình $\left( * \right)$ có 2 nghiệm âm phân biệt khác $ - 1$
$ \Leftrightarrow \left\{ \begin{gathered} \Delta > 0 \hfill \\ - \dfrac{b}{a} < 0 \hfill \\ \dfrac{c}{a} > 0 \hfill \\ y\left( { - 1} \right) \ne 0 \hfill \\ \end{gathered} \right. $ $\Leftrightarrow \left\{ \begin{gathered} {\left( {m - 2} \right)^2} > 0 \hfill \\ m + 4 < 0 \hfill \\ 3\left( {m + 1} \right) > 0 \hfill \\ {\left( { - 1} \right)^2} - \left( {m + 4} \right)\left( { - 1} \right) + 3\left( {m + 1} \right) \ne 0 \hfill \\ \end{gathered} \right. $ $\Leftrightarrow \left\{ \begin{gathered} m \ne 2 \hfill \\ m < - 4 \hfill \\ m > - 1 \hfill \\ m \ne - 2 \hfill \\ \end{gathered} \right. $ $\Leftrightarrow m \in \emptyset $
Tìm $m$ để đồ thị hàm số $y = {x^3} - 3{x^2} + 2$ cắt đường thẳng $y = m\left( {x - 1} \right)$ tại ba điểm phân biệt có hoành độ ${x_1},{x_2},{x_3}$ thỏa mãn $x_1^2 + x_2^2 + x_3^2 = 5$.
Phương trình hoành độ giao điểm:
${x^3} - 3{x^2} + 2 = m\left( {x - 1} \right) \Leftrightarrow \left( {x - 1} \right)\left( {{x^2} - 2x - 2 - m} \right) = 0 $
$\Leftrightarrow \left[ \begin{gathered} x = 1 \hfill \\ {x^2} - 2x - 2 - m = 0\left( * \right) \hfill \\ \end{gathered} \right.$
Để hai đồ thị hàm số cắt nhau tại ba điểm phân biệt thì phương trình hoành độ có 3 nghiệm phân biệt
$ \Leftrightarrow \left( * \right)$ có 2 nghiệm phân biệt khác $1 \Leftrightarrow \left\{ \begin{gathered} \Delta ' = 1 + 2 + m > 0 \hfill \\ 1 - 2 - 2 - m \ne 0 \hfill \\ \end{gathered} \right. \Leftrightarrow m > - 3$
Gọi ${x_1} = 1,{x_2},{x_3}$ lần lượt là nghiệm của phương trình $\left( * \right) \Rightarrow {x_2} + {x_3} = 2;{x_2}{x_3} = - 2 - m$
Ta có: $x_1^2 + x_2^2 + x_3^2 = 5 \Leftrightarrow {\left( {{x_2} + {x_3}} \right)^2} - 2{x_2}{x_3} = 4 $
$\Leftrightarrow 4 - 2\left( { - 2 - m} \right) = 4 \Leftrightarrow m = - 2$
Tìm điều kiện của $m$ để đồ thị hàm số $\left( {{C_m}} \right):y = {x^4} - m{x^2} + m - 1$ cắt trục hoành tại $4$ điểm phân biệt.
Xét phương trình hoành độ giao điểm ${x^4} - m{x^2} + m - 1 = 0$.
Đặt $t = {x^2},t \geqslant 0$ ta được phương trình ${t^2} - mt + m - 1 = 0$.
Để đồ thị hàm số $\left( {{C_m}} \right):y = {x^4} - m{x^2} + m - 1$ cắt trục hoành tại 4 điểm phân biệt thì phương trình ${t^2} - mt + m - 1 = 0$ phải có hai nghiệm dương phân biệt
$ \Leftrightarrow \left\{ \begin{gathered} \Delta > 0 \hfill \\ S > 0 \hfill \\ P > 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} {m^2} - 4m + 4 > 0 \hfill \\ m > 0 \hfill \\ m - 1 > 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} m \ne 2 \hfill \\ m > 1 \hfill \\ \end{gathered} \right.$
Cho hàm số $y = {x^4} - 2\left( {2m + 1} \right){x^2} + 4{m^2}$$\left( 1 \right)$. Các giá trị của tham số $m$ để đồ thị hàm số $\left( 1 \right)$ cắt trục hoành tại $4$ điểm phân biệt có hoành độ ${x_1},{x_2},{x_3},{x_4}$ thoả mãn ${x_1}^2 + {x_2}^2 + {x_3}^2 + {x_4}^2 = 6$
Đặt ${x^2} = t\left( {t \geqslant 0} \right)$
Phương trình ${x^4} - 2\left( {2m + 1} \right){x^2} + 4{m^2} = 0$ có 4 nghiệm phân biệt thỏa mãn $x_1^2 + x_2^2 + x_3^2 + x_4^2 = 6$$ \Leftrightarrow {t^2} - 2\left( {2m + 1} \right)t + 4{m^2} = 0$ có hai nghiệm phân biệt dương thỏa mãn $2{t_1} + 2{t_2} = 6$ hay ${t_1} + {t_2} = 3$
\( \Leftrightarrow \left\{ \begin{gathered}S > 0 \hfill \\P > 0 \hfill \\\Delta ' > 0 \hfill \\ \end{gathered} \right.\) $\Leftrightarrow \left\{ \begin{gathered} 2(2m + 1) > 0 \hfill \\ 4{m^2} > 0 \hfill \\ {\left( {2m + 1} \right)^2} - 4{m^2} > 0 \hfill \\ \end{gathered} \right. \Leftrightarrow 2\left( {2m + 1} \right) = 3$$ \Leftrightarrow m = \dfrac{1}{4}$
Cho hàm số $y = f\left( x \right)$ xác định trên $R\backslash \left\{ { - 1;\,1} \right\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên sau:
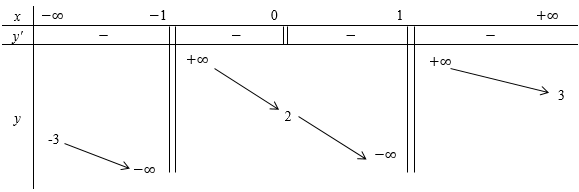
Tìm tất cả các giá trị thực của tham số m sao cho đường thẳng $y = 2m + 1$ cắt đồ thị hàm số $y = f\left( x \right)$ tại hai điểm phân biệt.
Quan sát BBT ta thấy đường thẳng $y = 2m + 1$ cắt đồ thị hàm số $y = f\left( x \right)$ tại hai điểm phân biệt $ \Leftrightarrow \left[ \begin{gathered}2m + 1 < - 3 \hfill \\ 2m + 1 > 3 \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} m < - 2 \hfill \\ m > 1 \hfill \\ \end{gathered} \right.$ .
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Với các giá trị nào của tham số m thì phương trình \(f\left( {\left| x \right|} \right) = 3m + 1\) có bốn nghiệm phân biệt.
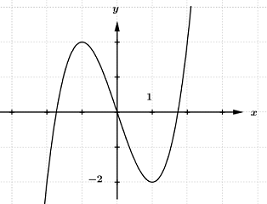
Dựa vào đồ thị hàm số \(y = f\left( x \right)\) ta suy ra được đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) như sau:
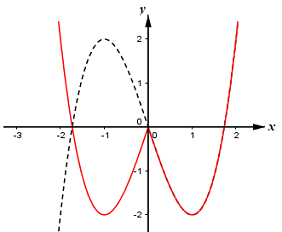
Số nghiệm của phương trình \(f\left( {\left| x \right|} \right) = 3m + 1\) là số giao điểm của đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) và đường thẳng \(y = 3m + 1\) song song với trục hoành.
Do đó để phương trình \(f\left( {\left| x \right|} \right) = 3m + 1\) có 4 nghiệm phân biệt thì \( - 2 < 3m + 1 < 0 \Leftrightarrow - 1 < m < - \dfrac{1}{3}\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên. Số nghiệm của phương trình \(\left| {f\left( x \right)} \right| = 2\) là:
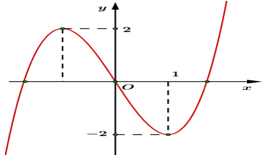
Ta có \(\left| {f\left( x \right)} \right| = 2 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = 2\\f\left( x \right) = - 2\end{array} \right.\)
Với \(f\left( x \right) = 2\) thì đường thẳng \(y = 2\) cắt đồ thị hàm số tại 2 điểm phân biệt.
Với \(f\left( x \right) = - 2\) thì đường thẳng \(y = - 2\) cắt đồ thị hàm số tại 2 điẻm phân biệt.
Vậy tổng có tất cả 4 nghiệm phân biệt.
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Số nghiệm của phương trình \(f\left( x \right) = 3\) là:
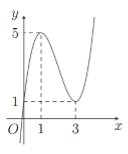
Đồ thị hàm số cắt đường thẳng \(y = 3\) tại 3 điểm phân biệt\( \Rightarrow f\left( x \right) = 3\) có 3 nghiệm phân biệt.
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( {\left| {\dfrac{{3\sin x - \cos x - 1}}{{2\cos x - \sin x + 4}}} \right|} \right) = f\left( {{m^2} + 4m + 4} \right)\) có nghiệm?
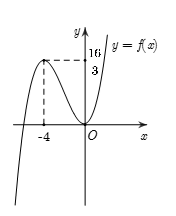
Vì \( - 1 \le \sin x \le 1; - 1 \le \cos x \le 1\) nên \(2\cos x - \sin x > - 3 \Rightarrow 2\cos x - \sin x + 4 > 0\)
Đặt \(\dfrac{{3\sin x - \cos x - 1}}{{2\cos x - \sin x + 4}} = t \Leftrightarrow 3\sin x - \cos x - 1 = t\left( {2\cos x - \sin x + 4} \right)\)
\( \Leftrightarrow \cos x\left( {2t + 1} \right) - \sin x\left( {t + 3} \right) = - 4t - 1\)
Phương trình trên có nghiệm khi \({\left( {2t + 1} \right)^2} + {\left( {t + 3} \right)^2} \ge {\left( { - 4t - 1} \right)^2}\)
\( \Leftrightarrow 5{t^2} + 10t + 10 \ge 16{t^2} + 8t + 1\) \( \Leftrightarrow 11{t^2} - 2t - 9 \le 0 \Leftrightarrow - \dfrac{9}{{11}} \le t \le 1 \Rightarrow 0 \le \left| t \right| \le 1\)
Từ đồ thị hàm số ta thấy hàm số \(f\left( x \right)\) đồng biến trên \(\left( {0;1} \right)\)
Nên phương trình \(f\left( x \right) = f\left( {\left| t \right|} \right)\) với \(t \in \left[ {0;1} \right]\) có nghiệm duy nhất khi \(x = \left| t \right| \Rightarrow 0 \le x \le 1\)
Do đó phương trình \(f\left( {\left| {\dfrac{{3\sin x - \cos x - 1}}{{2\cos x - \sin x + 4}}} \right|} \right) = f\left( {{m^2} + m + 4} \right)\) có nghiệm
\( \Leftrightarrow \left| t \right| = {m^2} + 4m + 4\) có nghiệm với \(0 \le \left| t \right| \le 1\)
\( \Leftrightarrow 0 \le {m^2} + 4m + 4 \le 1 \Leftrightarrow {\left( {m + 2} \right)^2} \le 1 \Leftrightarrow - 3 \le m \le - 1\)
Mà \(m \in \mathbb{Z}\) nên \(m \in \left\{ { - 3; - 2; - 1} \right\}\). Vậy có 3 giá trị của \(m\) thỏa mãn yêu cầu.
Mình cần đánh giá cho biểu thức này em nhé :\(\left( {2\cos x - \sin x + 4} \right)\)
Mục đích đánh giá là để có thể quy đồng sau khi đặt t. Từ đó tìm điều kiện cho t.
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau
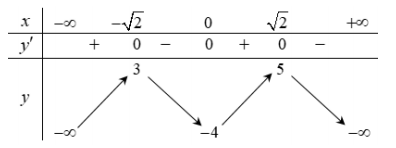
Có bao nhiêu giá trị nguyên của tham số \(m\) sao cho phương trình \(2f\left( {\sin x - \cos x} \right) = m - 1\) có hai nghiệm
phân biệt trên khoảng \(\left( { - \dfrac{\pi }{4};\dfrac{{3\pi }}{4}} \right)?\)
Ta có \(\sin x - \cos x = \sqrt 2 \sin \left( {x - \dfrac{\pi }{4}} \right)\) mà \(x \in \left( { - \dfrac{\pi }{4};\dfrac{{3\pi }}{4}} \right) \Rightarrow \sin \left( {x - \dfrac{\pi }{4}} \right) \in \left( { - 1;1} \right)\)
Đặt \(\sin x - \cos x = t\,\) thì \(t \in \left( { - \sqrt 2 ;\sqrt 2 } \right)\)
Đưa về bài toán tìm \(m\) để phương trình \(2f\left( t \right) = m - 1\) có hai nghiệm phân biệt trên khoảng \(\left( { - \sqrt 2 ;\sqrt 2 } \right)\)
Ta có \(2f\left( t \right) = m - 1 \Leftrightarrow f\left( t \right) = \dfrac{{m - 1}}{2}\)
Từ BBT ta suy ra \( - 4 < \dfrac{{m - 1}}{2} < 3 \Leftrightarrow - 8 < m - 1 < 6 \Leftrightarrow - 7 < m < 7\) mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 6; - 5;...;0;1;2;...;6} \right\}\)
Nên có \(13\) giá trị của \(m\) thỏa mãn đề bài.
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên. Tìm tất cả các giá trị thực của tham số \(m\) để phương trình \(f\left( x \right) = {\log _2}m\) có hai nghiệm phân biệt.
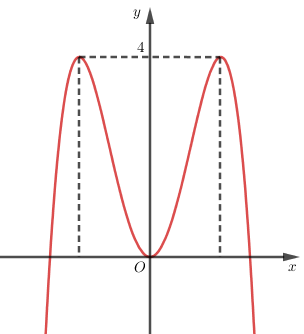
Phương trình \(f\left( x \right) = {\log _2}m\) có hai nghiệm phân biệt \( \Leftrightarrow \) đường thẳng \(y = {\log _2}m\) cắt đồ thị hàm số đã cho tại hai điểm phân biệt \( \Leftrightarrow \left[ \begin{array}{l}{\log _2}m = 4\\{\log _2}m < 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = {2^4}\\0 < m < {2^0}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 16\\0 < m < 1\end{array} \right.\).
Cho hàm số bậc ba \(y = f\left( x \right)\) có bảng biến thiên trong hình dưới:
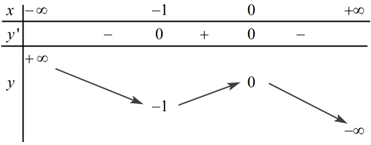
Số nghiệm của phương trình \(f\left( x \right) = - 0,5\) là:
Số nghiệm của phương trình \(f\left( x \right) = - 0,5\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = - 0,5.\)
Ta có BBT:
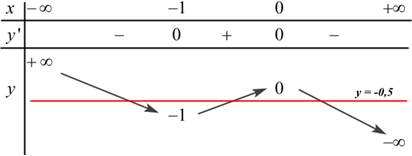
Dựa vào BBT ta thấy đường thẳng \(y = - 0,5\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 3 điểm phân biệt.
\( \Rightarrow \) Phương trình \(f\left( x \right) = - 0,5\) có \(3\) nghiệm phân biệt.

