Bài toán tương giao đồ thị
Kỳ thi ĐGNL ĐHQG Hồ Chí Minh
Cho hàm số y=f(x) liên tục trên R và có bảng biến thiên như hình vẽ
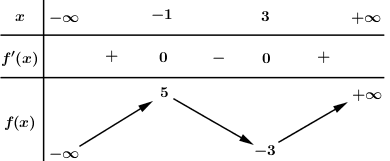
Phương trình |f(3x+1)−2|=5 có bao nhiêu nghiệm?
Đặt t=3x+1.
Dễ thấy với mỗi x chỉ có một x và ngược lại.
Do đó số nghiệm x của phương trình đã cho bằng số nghiệm t của phương trình |f(t)−2|=5
Ta có:
|f(t)−2|=5
⇔[f(t)−2=5f(t)−2=−5⇔[f(t)=7(1)f(t)=−3(2)
Từ bbt ta thấy,
+) Đường thẳng y=7 cắt đồ thị hàm số tại duy nhất 1 điểm nên (1) có 1 nghiệm.
+) Đường thẳng y=−3 cắt đồ thị hàm số tại 2 điểm nên (2) có 2 nghiệm.
Dễ thấy các nghiệm của (1) và (2) phân biệt.
Vậy phương trình đã cho có tất cả 3 nghiệm.
Có tất cả bao nhiêu giá trị nguyên thuộc đoạn [−2020;2020] của tham số m để đường thẳng y=x+m cắt đồ thị hàm số y=2x−3x−1 tại hai điểm phân biệt?
TXĐ: D=R∖{1}.
Xét phương trình hoành độ giao điểm:
2x−3x−1=x+m(x≠1)⇔2x−3=(x−1)(x+m)⇔2x−3=x2+mx−x−m⇔x2+(m−3)x−m+3=0(∗)
Để để đường thẳng y=x+m cắt đồ thị hàm số y=2x−3x−1 tại hai điểm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt khác 1
⇒{Δ=(m−3)2−4(−m+3)>01+(m−3).1−m+3≠0⇔{m2−6m+9+4m−12>01≠0(luondung)⇔m2−2m−3>0⇔[m>3m<−1
Kết hợp điều kiện bài toán ta suy ra m∈[−2020;−1)∪(3;2020], m∈Z.
Vậy có 2019 + 2017 = 4036 giá trị của m thỏa mãn yêu cầu bài toán.
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên. Số nghiệm của phương trình f(1−f(x))=2 là:
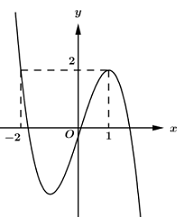
Đặt t=1−f(x), phương trình trở thành f(t)=2.
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y=f(t) và đường thẳng y=2.
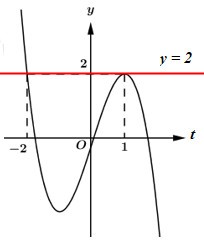
Dựa vào đồ thị hàm số ta thấy f(t)=2⇔[t=1t=−2 ⇔[1−f(x)=11−f(x)=−2⇔[f(x)=0(1)f(x)=3(2).
+ Số nghiệm của phương trình (1) là số giao điểm của đồ thị hàm số y=f(x) và đường thẳng y=0 nên phương trình (1) có 3 nghiệm phân biệt.
+ Số nghiệm của phương trình (2) là số giao điểm của đồ thị hàm số y=f(x) và đường thẳng y=3 nên phương trình (1) có 1 nghiệm duy nhất.
Vậy phương trình đã cho có tất cả 4 nghiệm.
Cho hàm số y=f(x) có bảng biến thiên:
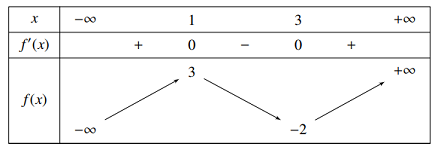
Tìm tất cả các giá trị của m để bất phương trình f(3−x2)≥m vô nghiệm?
Đặt t=3−x2, ta có: x2≥0,∀x∈R⇒t=3−x2≤3,∀x∈R⇒t∈(−∞;3].
Bất phương trình f(3−x2)≥m vô nghiệm khi và chỉ khi f(t)≥m vô nghiệm với mọi t∈(−∞;3].
Từ BBT của hàm số y=f(x) ta thấy: f(t)≥m vô nghiệm với t∈(−∞;3] khi m>3.
Vậy m>3.
Cho hàm số y=x3+2mx2+(m+3)x+4(Cm). Giá trị của tham số m để đường thẳng (d):y=x+4 cắt (Cm) tại ba điểm phân biệt A(0;4),B,C sao cho tam giác KBC có diện tích bằng 8√2 với điểm K(1;3) là:
+ Xét phương trình hoành độ giao điểm của đồ thị và đường thẳng ta có:
x3+2mx2+(m+3)x+4=x+4⇔x3+2mx2+(m+2)x=0⇔x(x2+2mx+m+2)=0⇔[x=0x2+2mx+m+2=0(1)
Để (d) cắt (Cm) tại 3 điểm phân biệt thì phương trình (1) có 2 nghiệm phân biệt khác 0
⇒{Δ;>00+2m.0+m+2≠0⇔{m2−m−2>0m≠−2⇔{[m>2m<−1m≠2 .
Gọi x1;x2 là 2 nghiệm phân biệt của phương trình (1) ⇒B(x1;x1+4);C(x2;x2+4).
Khi đó áp dụng định lí Vi-ét ta có: {x1+x2=−2mx1.x2=m+2.
Ta có: SKBC=12.d(K,BC).BC.
Phương trình đường thẳng (d):y=x+4⇔x−y+4=0.
Vì B,C thuộc đường thẳng (d) nên ta có: d(K,BC)=d(K;d)=|1−3+4|√12+(−1)2=√2.
BC=√(x2−x1)2+(x2+4−x1−4)2BC=√2(x1−x2)2BC=√2.√(x1+x2)2−4x1x2BC=√2.√4m2−4(m+2)BC=2√2.√m2−m−2
Theo bài ra ta có:
SKBC=8√2⇔12.√2.2√2√m2−m−2=8√2⇔√m2−m−2=4√2⇔m2−m−2=32⇔m2−m−34=0⇔m=1±√1372(tm)
Vậy m=1±√1372.
Đề thi THPT QG - 2021 - mã 101
Đồ thị hàm số y=−x4+4x2−3 cắt trục tung tại điểm có tung độ bằng
Đồ thị hàm số y=−x4+4x2−3 cắt trục tung ⇒x=0
Với x=0 thay vào hàm số ⇒y=−3.

