1. Định nghĩa
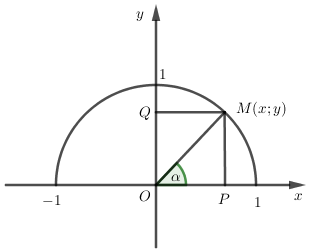
Trên nửa đường tròn đơn vị tâm \(O\), ta xác định điểm $M$ sao cho \(\alpha = \widehat {xOM}\left( {{0^0} \le \alpha \le {{180}^0}} \right)\). Giả sử điểm $M\left( {x;y} \right)$. Khi đó:
\({\rm{sin}}\alpha = y;\,\,{\rm{cos}}\alpha = {\rm{x}};\) \({\rm{tan}}\alpha = \dfrac{y}{x}\,\,(\alpha \ne {90^0});\) \({\rm{ cot}}\alpha = \;\;\dfrac{x}{y}\;(\alpha \ne {0^0},\alpha \ne {180^0})\)
Các số \(\sin \alpha ,\,\cos \alpha ,\,\tan \alpha ,\,\cot \alpha \) được gọi là giá trị lượng giác của góc \(\alpha \).
Từ định nghĩa ta có:
Gọi $P,Q$ lần lượt là hình chiếu của $M$ lên trục $Ox,Oy$ khi đó \(M\left( {\overline {OP} ;\overline {OQ} } \right)\).
Với \({0^0} \le \alpha \le {180^0}\) ta có \(0 \le \sin \alpha \le 1;\,\, - 1 \le \cos \alpha \le 1\)
Dấu của giá trị lượng giác:
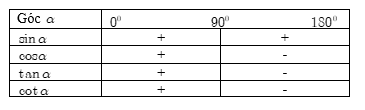
2. Tính chất
a) Góc phụ nhau
\(\begin{array}{l}\sin ({90^0} - \alpha ) = \cos \alpha & \\\cos ({90^0} - \alpha ) = \sin \alpha \,\\\tan ({90^0} - \alpha ) = \cot \alpha \\\cot ({90^0} - \alpha ) = \tan \alpha \end{array}\)
b) Góc bù nhau
\(\begin{array}{l}\sin ({180^0} - \alpha ) = \sin \alpha & \\\cos ({180^0} - \alpha ) = - \cos \alpha \,\\\tan ({180^0} - \alpha ) = - \tan \alpha \\\cot ({180^0} - \alpha ) = - \cot \alpha \end{array}\)
3. Giá trị lượng giác của các góc đặc biệt
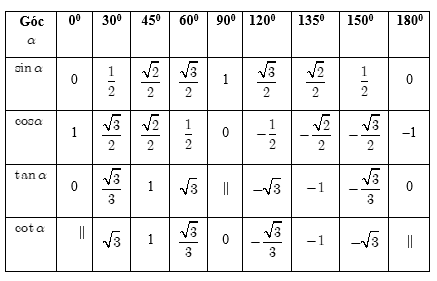
4. Các hệ thức lượng giác cơ bản
\(\begin{array}{l}1)\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }}(\alpha \ne {90^0})\\2)\cot \alpha = \dfrac{{\cos \alpha }}{{\sin \alpha }}(\alpha \ne {0^0};{180^0})\\3)\tan \alpha .\cot \alpha = 1(\alpha \ne {0^0};{90^0};{180^0})\\4){\sin ^2}\alpha + {\cos ^2}\alpha = 1\\5)1 + {\tan ^2}\alpha = \dfrac{1}{{{{\cos }^2}\alpha }}(\alpha \ne {90^0})\\6)1 + {\cot ^2}\alpha = \dfrac{1}{{{{\sin }^2}\alpha }}(\alpha \ne {0^0};{180^0})\end{array}\)

