1. Vectơ pháp tuyến và véc tơ chỉ phương của đường thẳng
Định nghĩa: Cho đường thẳng \(\Delta \)
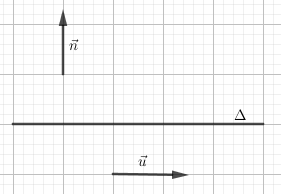
- Vectơ \(\overrightarrow n \ne \overrightarrow 0 \) gọi là vectơ pháp tuyến (VTPT) của \(\Delta \) nếu giá của \(\overrightarrow n \) vuông góc với \(\Delta \)
- Vectơ \(\overrightarrow u \ne \overrightarrow 0 \) gọi là vectơ chỉ phương (VTCP) của đường thẳng \(\Delta \) nếu giá của nó song song hoặc trùng với \(\Delta \)
Nhận xét:
- Nếu \(\overrightarrow n \left( {\overrightarrow u } \right)\) là VTPT (VTCP) của \(\Delta \) thì \(k\overrightarrow n \left( {k \ne 0} \right)\) hoặc \(k\overrightarrow u \) cũng là VTPT (VTCP) của \(\Delta \)
- VTPT và VTCP vuông góc với nhau: \(\overrightarrow {{n_\Delta }} .\overrightarrow {{u_\Delta }} = 0\)
- Nếu \(\Delta \) có VTCP \(\overrightarrow u = (a;b)\) thì \(\overrightarrow n = ( - b;a)\) là một VTPT của \(\Delta \)
2. Phương trình tổng quát, tham số của đường thẳng
a) Phương trình tổng quát
Cho đường thẳng \(\Delta \) đi qua \({M_0}({x_0};{y_0})\) và có VTPT \(\overrightarrow n = (a;b)\). Khi đó:
\(\Delta :a(x - {x_0}) + b(y - {y_0}) = 0\)
Phương trình trên được gọi là phương trình tổng quát của đường thẳng \(\Delta \)
- Nếu đường thẳng \(\Delta :ax + by + c = 0\) thì \(\overrightarrow n = (a;b)\) là VTPT của \(\Delta \).
- Điểm \(M\left( {{x_0};{y_0}} \right)\) thuộc \(\Delta :ax + by + c = 0 \) \(\Leftrightarrow a{x_0} + b{y_0} + c = 0\)
b) Phương trình tham số của đường thẳng:
Cho đường thẳng \(\Delta \) đi qua \({M_0}({x_0};{y_0})\) và \(\overrightarrow u = (a;b)\) là VTCP. Khi đó:
\(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\end{array} \right.{\rm{ }}t \in R\,\,\,\left( 1 \right)\)
Hệ (1) gọi là phương trình tham số của đường thẳng \(\Delta ,t\) gọi là tham số
Nhận xét : Nếu \(\Delta \) có phương trình tham số là (1) thì \(A \in \Delta \Leftrightarrow A({x_0} + at;{y_0} + bt)\)
c) Phương trình chính tắc.
Cho đường thẳng \(\Delta \) đi qua \({M_0}({x_0};{y_0})\) và \(\overrightarrow u = (a;b)\) (với \(a \ne 0,\,\,b \ne 0\)) là vectơ chỉ phương thì phương trình \(\dfrac{{x - {x_0}}}{a} = \dfrac{{y - {y_0}}}{b}\) được gọi là phương trình chính tắc của đường thẳng \(\Delta \).
3. Vị trí tương đối của hai đường thẳng
Cho hai đường thẳng \({d_1}:{a_1}x + {b_1}y + {c_1} = 0;\) \({\rm{ }}{d_2}:{a_2}x + {b_2}y + {c_2} = 0\)
\({d_1}\) cắt ${d_2}$ khi và chỉ khi \(\left| {\begin{array}{*{20}{c}}{{a_1}}&{{b_1}}\\{{a_2}}&{{b_2}}\end{array}} \right| \ne 0\)
\({d_1}//{d_2}\) khi và chỉ khi \(\left| {\begin{array}{*{20}{c}}{{a_1}}&{{b_1}}\\{{a_2}}&{{b_2}}\end{array}} \right| = 0\) và \(\left| {\begin{array}{*{20}{c}}{{b_1}}&{{c_1}}\\{{b_2}}&{{c_2}}\end{array}} \right| \ne 0\), hoặc \(\left| {\begin{array}{*{20}{c}}{{a_1}}&{{b_1}}\\{{a_2}}&{{b_2}}\end{array}} \right| = 0\) và \(\left| {\begin{array}{*{20}{c}}{{c_1}}&{{a_1}}\\{{c_2}}&{{a_2}}\end{array}} \right| \ne 0\)
\({d_1} \equiv {d_2}\) khi và chỉ khi \(\left| {\begin{array}{*{20}{c}}{{a_1}}&{{b_1}}\\{{a_2}}&{{b_2}}\end{array}} \right| = \left| {\begin{array}{*{20}{c}}{{b_1}}&{{c_1}}\\{{b_2}}&{{c_2}}\end{array}} \right| = \left| {\begin{array}{*{20}{c}}{{c_1}}&{{a_1}}\\{{c_2}}&{{a_2}}\end{array}} \right| = 0\)
Với trường hợp \({a_2}.{b_2}.{c_2} \ne 0\) khi đó
+ Nếu \(\dfrac{{{a_1}}}{{{a_2}}} \ne \dfrac{{{b_1}}}{{{b_2}}}\) thì hai đường thẳng cắt nhau.
+ Nếu \(\dfrac{{{a_1}}}{{{a_2}}} = \dfrac{{{b_1}}}{{{b_2}}} \ne \dfrac{{{c_1}}}{{{c_2}}}\) thì hai đường thẳng song song nhau.
+ Nếu \(\dfrac{{{a_1}}}{{{a_2}}} = \dfrac{{{b_1}}}{{{b_2}}} = \dfrac{{{c_1}}}{{{c_2}}}\) thì hai đường thẳng trùng nhau.
+ Nếu \({a_1}{a_2} + {b_1}{b_2} = 0\) thì hai đường thẳng vuông góc.

