1. Hàm số cho dưới dạng khoảng
- Là hàm số có dạng: \(y = \left\{ \begin{array}{l}f\left( x \right)\,\,\,khi\,\,\,x \in D\\g\left( x \right)\,\,\,khi\,\,\,x \in D'\end{array} \right.\)
- Vẽ đồ thị hàm số:
+ Vẽ đồ thị hàm số \(y = f\left( x \right)\) trên \(D\).
+ Vẽ đồ thị hàm số \(y = g\left( x \right)\) trên \(D'\).
+ Hợp hai đồ thị trên chính là đồ thị hàm số vần tìm.
Ví dụ: Vẽ đồ thị hàm số \(y = \left\{ \begin{array}{l}2x\,\,\,\,\,\,\,\,\,\,\,khi\,\,\,x > 1\\ - x + 2\,\,\,khi\,\,\,x \le 1\end{array} \right.\)
Ta vẽ các đồ thị hàm số \(y = 2x\) trên \(\left( {1; + \infty } \right)\) và \(y = - x + 2\) trên \(\left( { - \infty ;1} \right]\) như sau:
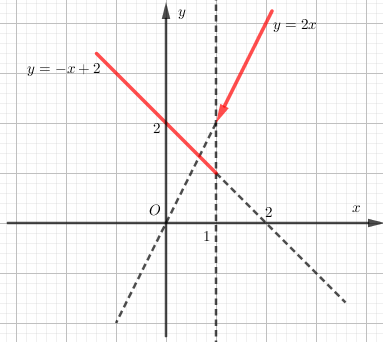
Phần đồ thị tô màu đỏ chính là đồ thị hàm số cần tìm.
Chú ý: Điểm mũi tên là thể hiện điểm \(\left( {1;2} \right)\) không thuộc đồ thị hàm số \(y = 2x\).
2. Hàm số có chứa dấu giá trị tuyệt đối
- Là hàm số dạng \(y = f\left( x \right)\), trong biểu thức \(f\left( x \right)\) có chứa dấu giá trị tuyệt đối.
- Vẽ đồ thị hàm số:
+ Biến đổi hàm số đã cho thành hàm số cho dưới dạng khoảng bằng cách phá dấu giá trị tuyệt đối kèm theo điều kiện của \(x\).
+ Vẽ đồ thị hàm số sau khi biến đổi ta được đồ thị hàm số cần tìm.
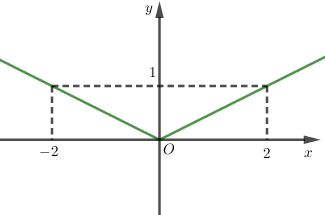
Ví dụ: Vẽ đồ thị hàm số \(y = \left| x \right| - 2\).
Ta có: \(y = \left| x \right| - 2 = \left\{ \begin{array}{l}x - 2\,\,\,\,khi\,\,\,x \ge 0\\ - x - 2\,khi\,\,\,x < 0\end{array} \right.\)
Vẽ đồ thị hàm số \(y = \left\{ \begin{array}{l}x - 2\,\,\,\,khi\,\,\,x \ge 0\\ - x - 2\,khi\,\,\,x < 0\end{array} \right.\) ta được:
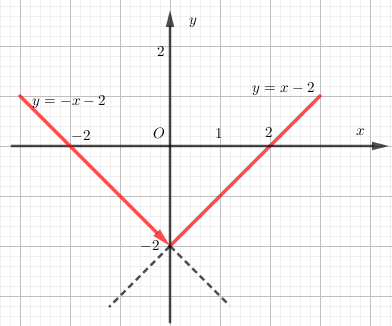
Phần đồ thị tô màu đỏ là đồ thị hàm số \(y = \left| x \right| - 2\).
Điểm mũi tên \(\left( {0; - 2} \right)\) thể hiện nó không thuộc đồ thị hàm số \(y = - x - 2\), tuy nhiên nó vẫn thuộc đồ thị hàm số \(y = x - 2\) nên khi hợp lại ta vẫn được đồ thị hàm số có đi qua điểm \(\left( {0; - 2} \right)\), tránh nhầm lẫn với ví dụ ở trên và kết luận điểm \(\left( {0; - 2} \right)\) không thuộc đồ thị hàm số là sai.
Chú ý: Khi vẽ hình, ta cũng có thể vẽ nét liền tại điểm \(\left( {0; - 2} \right)\) vì nó vẫn thuộc đồ thị hàm số.