1. Định nghĩa vectơ
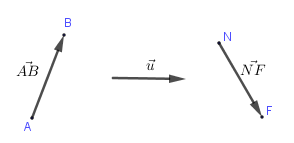
Vectơ là đoạn thẳng có hướng, nghĩa là trong hai điểm mút của đoạn thẳng đã chỉ rõ điểm nào là điểm đầu, điểm nào là điểm cuối.
Vectơ có điểm đầu là $A,$ điểm cuối là $B$ ta kí hiệu $\overrightarrow {AB} $
Vectơ còn được kí hiệu là: $\overrightarrow a ,{\rm{ }}\overrightarrow b ,{\rm{ }}\overrightarrow x ,{\rm{ }}\overrightarrow y ,...$
Vectơ – không là vectơ có điểm đầu trùng điểm cuối. Kí hiệu là \(\overrightarrow 0 \)
2. Hai vectơ cùng phương, cùng hướng
- Đường thẳng đi qua điểm đầu và điểm cuối của vectơ gọi là giá của vectơ
- Hai vectơ có giá song song hoặc trùng nhau gọi là hai vectơ cùng phương
- Hai vectơ cùng phương thì hoặc cùng hướng hoặc ngược hướng.
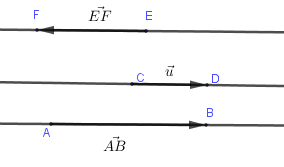
Ví dụ: Ở hình vẽ trên trên thì hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) cùng hướng còn \(\overrightarrow {EF} \) và \(\overrightarrow {CD} \) ngược hướng.
Đặc biệt: vectơ – không cùng hướng với mọi véc tơ.
3. Hai vectơ bằng nhau
- Độ dài đoạn thẳng $AB$ gọi là độ dài véc tơ $\overrightarrow {AB} $, kí hiệu $\left| {\overrightarrow {AB} } \right|$.
Vậy $\left| {\overrightarrow {AB} } \right| = AB$
- Hai vectơ bằng nhau nếu chúng cùng hướng và cùng độ dài.
- Hai vecto đối nhau nếu chúng ngược hướng và cùng độ dài.
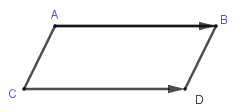
Ví dụ: Cho hình bình hành \(ABDC\) khi đó:
\(\overrightarrow {AB} = \overrightarrow {CD} \) vì chúng cùng hướng và cùng độ dài.
\(\overrightarrow {AB} \) và \(\overrightarrow {DC} \) là hai véc tơ đối nhau vì chúng ngược hướng và cùng độ dài.
Cho hai điểm \(A,B\) phân biệt, khi đó không tồn tại điểm \(M\) nào để \(\overrightarrow {MA} = \overrightarrow {MB} \)
Chứng minh:

Phản chứng:
Giả sử có điểm \(M\) sao cho \(\overrightarrow {MA} = \overrightarrow {MB} \).
Khi đó \(\overrightarrow {MA} ,\overrightarrow {MB} \) cùng hướng và cùng độ dài.
Vì \(\overrightarrow {MA} ,\overrightarrow {MB} \) cùng hướng nên \(M\) chỉ nằm trên đường thẳng \(AB\) và nằm ngoài hai điểm \(A,B\).
Như vậy thì chỉ xảy ra \(MA < MB\) hoặc \(MA > MB\) nên mâu thuẫn với giả thiết cùng độ dài.
Do đó không tồn tại điểm \(M\) thỏa mãn \(\overrightarrow {MA} = \overrightarrow {MB} \).
Tuy nhiên, nếu \(A,B\) trùng nhau thì ta lại có vô số điểm \(M\) thỏa mãn \(\overrightarrow {MA} = \overrightarrow {MB} \).

