1. Bất phương trình bậc nhất hai ẩn
a) Bất phương trình bậc nhất hai ẩn và miền nghiệm của nó.
- Bất phương trình bậc nhất hai ẩn x, y có dạng: $ax + by + c < 0,ax + by + c > 0,ax + by + c \le 0,ax + by + c \ge 0$ trong đó $a,b,c$ là những số thực đã cho, $a$ và $b$ không đồng thời bằng $0;x$ và $y$ là các ẩn số.
- Mỗi cặp số $\left( {{x_0};{y_0}} \right)$ sao cho $a{x_0} + b{y_0} < c$ gọi là một nghiệm của bất phương trình $ax + by + c < 0$.
- Nghiệm của các bất phương trình dạng $ax + by > c,ax + by \le c,ax + by \ge c$ cũng được định nghĩa tương tự.
- Tập hợp điểm biểu diễn các nghiệm của bất phương trình bậc nhất hai ẩn được gọi là miền nghiệm của bất phương trình.
b) Cách xác định miền nghiệm của bất phương trình bậc nhất hai ẩn.
Quy tắc thực hành biểu diễn hình học tập nghiệm (hay biểu diễn miền nghiệm) như sau:
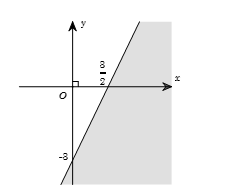
Bước 1. Vẽ đường thẳng $\left( d \right):ax + by + c = 0$
Bước 2. Xét một điểm $M\left( {{x_0};{y_0}} \right)$ không nằm trên $\left( d \right)$.
- Nếu $a{x_0} + b{y_0} + c < 0$ thì nửa mặt phẳng (không kể bờ $\left( d \right)$) chứa điểm $M$ là miền nghiệm của bất phương trình $ax + by + c < 0$.
- Nếu $a{x_0} + b{y_0} + c > 0$ thì nửa mặt phẳng (không kể bờ $\left( d \right)$) không chứa điểm $M$ là miền nghiệm của bất phương trình $ax + by + c > 0$.
Đối với các bất phương trình dạng $ax + by + c \le 0$ hoặc $ax + by + c \ge 0$ thì miền nghiệm là nửa mặt phẳng kể cả bờ.
2. Hệ bất phương trình bậc nhất hai ẩn
Tương tự hệ bất phương trình một ẩn, ta có hệ bất phương trình bậc nhất hai ẩn.
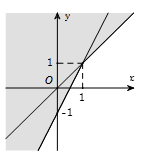
Trong mặt phẳng tọa độ, ta gọi tập hợp các điểm có tọa độ thỏa mãn mọi bất phương trình trong hệ là miền nghiệm của hệ.
Vậy miền nghiệm của hệ là giao các miền nghiệm của các bất phương trình trong hệ.
Để xác định miền nghiệm của hệ, ta dùng phương pháp biểu diễn hình học như sau:
- Bước 1: Xác định miền nghiệm của từng bất phương trình trong hệ và gạch bỏ miền còn lại.
- Bước 2: Tìm miền còn lại không bị gạch chính là miền nghiệm của hệ bất phương trình đã cho.
3. Ứng dụng vào bài toán tối ưu
Bài toán: Tìm giá trị lớn nhất, nhỏ nhất của biểu thức \(T\left( {x,y} \right) = ax + by\) với \(\left( {x;y} \right)\) nghiệm đúng một hệ bất phương trình bậc nhất hai ẩn cho trước.
- Bước 1: Xác định miền nghiệm của hệ bất phương trình đã cho. Kết quả thường được miền nghiệm \(S\) là đa giác.
- Bước 2: Tính giá trị của \(T\) tương ứng với \(\left( {x;y} \right)\) là tọa độ của các đỉnh của đa giác.
- Bước 3: Kết luận:
\( \bullet \) Giá trị lớn nhất của \(T\) là số lớn nhất trong các giá trị tìm được.
\( \bullet \) Giá trị nhỏ nhất của \(T\) là số nhỏ nhất trong các giá trị tìm được.