I. HÀM SỐ
1. Định nghĩa
Cho \(D \subset \mathbb{R},\,\,D \ne \emptyset \). Hàm số \(f\) xác định trên $D$ là một qui tắc đặt tương ứng mỗi số \(x \in D\) với một và chỉ một số \(y \in \mathbb{R}\).
2. Tập xác định
Tập xác định của hàm số $y = f\left( x \right)$ là tập hợp tất cả các số thực $x$ sao cho biểu thức \(f\left( x \right)\) có nghĩa.
3. Sự biến thiên
Cho hàm số \(f\) xác định trên \(K\).
Hàm số $y = f\left( x \right)$ đồng biến (tăng) trên \(K\) nếu \(\forall {x_1},{x_2} \in K:{x_1} < {x_2} \Rightarrow f({x_1}) < f({x_2})\)
Hàm số $y = f\left( x \right)$ nghịch biến (giảm) trên \(K\) nếu \(\forall {x_1},{x_2} \in K:{x_1} < {x_2} \Rightarrow f({x_1}) > f({x_2})\)
4. Tính chẵn lẻ
Cho hàm số $y = f\left( x \right)$ có tập xác định $D$.
Hàm số \(f\) được gọi là hàm số chẵn nếu với \(\forall x \in D\) thì \( - x \in D\) và $f\left( {-x} \right) = f\left( x \right)$ .
Hàm số \(f\) được gọi là hàm số lẻ nếu với \(\forall x \in D\) thì \( - x \in D\) và $f\left( {-x} \right) = - f\left( x \right)$ .
Chú ý: + Đồ thị của hàm số chẵn nhận trục tung làm trục đối xứng.
+ Đồ thị của hàm số lẻ nhận gốc toạ độ làm tâm đối xứng.
5. Tịnh tiến đồ thị hàm số
Định lý: Cho \(\left( G \right)\) là đồ thị của $y = f\left( x \right)$ và \(p > 0,\,\,q > 0\); ta có
Tịnh tiến \(\left( G \right)\) lên trên $q$ đơn vị thì được đồ thị $y = f\left( x \right) + q$
Tịnh tiến \(\left( G \right)\) xuống dưới $q$ đơn vị thì được đồ thị $y = f\left( x \right)-q$
Tịnh tiến \(\left( G \right)\) sang trái $p$ đơn vị thì được đồ thị $y = f\left( {x + p} \right)$
Tịnh tiến \(\left( G \right)\) sang phải $p$ đơn vị thì được đồ thị $y = f\left( {x-p} \right)$
II. HÀM SỐ BẬC NHẤT
1. Định nghĩa
Hàm số bậc nhất là hàm số có dạng \(y = ax + b\) \((a \ne 0)\).
2. Sự biến thiên
\( \bullet {\rm{ }}\)TXĐ: \(D = \mathbb{R}\)
\( \bullet {\rm{ }}\)Hàm số đồng biến khi \(a > 0\) và nghịch biến khi \(a < 0\)
Bảng biến thiên:

3. Đồ thị
Đồ thị của hàm số \(y = ax + b\) \((a \ne 0)\) là một đường thẳng \(d\) có hệ số góc bằng \(a\), cắt trục hoành tại \(A\left( { - \dfrac{b}{a};0} \right)\) và trục tung tại \(B\left( {0;b} \right)\)
Hệ số góc của đường thẳng \(d\) là \(a = \tan \alpha \) với \(\alpha \) là góc tạo bởi \(d\) và \(Ox\)
Chú ý:
\( \bullet {\rm{ }}\)Nếu \(a = 0 \Rightarrow y = b\) là hàm số hằng, đồ thị là đường thẳng song song hoặc trùng với trục hoành.
\( \bullet {\rm{ }}\) Phương trình \(x = a\) cũng là một đường thẳng(nhưng không phải là một hàm số) vuông góc với trục tọa độ và cắt tại điểm có hoành độ bằng a.
\( \bullet {\rm{ }}\)Cho đường thẳng $d$ có hệ số góc \(k\), $d$ đi qua điểm \(M\left( {{x_0};{y_0}} \right)\), khi đó phương trình của đường thẳng \(d\) là: \(y - {y_0} = a\left( {x - {x_0}} \right)\).
4. Đồ thị của hàm số chứa dấu giá trị tuyệt đối
Vẽ đồ thị \(\left( C \right)\) của hàm số \(y = \left| {ax + b} \right|\) ta làm như sau
Cách 1: Vẽ \(\left( {{C_1}} \right)\) là đường thẳng \(y = ax + b\) với phần đồ thị sao cho hoành độ \(x\) thỏa mãn $x \ge - \dfrac{b}{a}$ , Vẽ \(\left( {{C_2}} \right)\) là đường thẳng \(y = - ax - b\) lấy phần đồ thị sao cho $x < - \dfrac{b}{a}$. Khi đó \(\left( C \right)\) là hợp của hai đồ thị \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\).
Cách 2: Vẽ đường thẳng \(y = ax + b\) và \(y = - ax - b\) rồi xóa đi phần đường thẳng nằm dưới trục hoành. Phần đường thẳng nằm trên trục hoành chính là \(\left( C \right)\).
Chú ý:
\( \bullet \) Biết trước đồ thị $\left( C \right):y = f\left( x \right)$ khi đó đồ thị $\left( {{C_1}} \right):y = f\left( {\left| x \right|} \right)$ là gồm phần :
- Giữ nguyên đồ thị $\left( C \right)$ ở bên phải trục tung;
- Lấy đối xứng đồ thị $\left( C \right)$ ở bên phải trục tung qua trục tung.
\( \bullet \) Biết trước đồ thị $\left( C \right):y = f\left( x \right)$ khi đó đồ thị $\left( {{C_2}} \right):y = \left| {f\left( x \right)} \right|$ là gồm phần:
- Giữ nguyên đồ thị $\left( C \right)$ ở phía trên trục hoành
- Lấy đối xứng phần đồ thị $\left( C \right)$ phía dưới trục hoành qua trục hoành.
III. HÀM SỐ BẬC HAI
1. Định nghĩa
Hàm số bậc hai là hàm số có dạng \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\)
2. Sự biến thiên
\( \bullet {\rm{ }}\)TXĐ: \(D = \mathbb{R}\)
\( \bullet {\rm{ }}\)Khi \(a > 0\) hàm số đồng biến trên \(\left( { - \dfrac{b}{{2a}}; + \infty } \right)\), nghịch biến trên \(\left( { - \infty ; - \dfrac{b}{{2a}}} \right)\) và có giá trị nhỏ nhất là \( - \dfrac{\Delta }{{4a}}\) khi \(x = - \dfrac{b}{{2a}}\). Khi \(a < 0\) hàm số đồng biến trên \(\left( { - \infty ; - \dfrac{b}{{2a}}} \right)\), nghịch biến trên \(\left( { - \dfrac{b}{{2a}}; + \infty } \right)\) và có giá trị lớn nhất là \( - \dfrac{\Delta }{{4a}}\) khi \(x = - \dfrac{b}{{2a}}\)
Bảng biến thiên:

3. Đồ thị
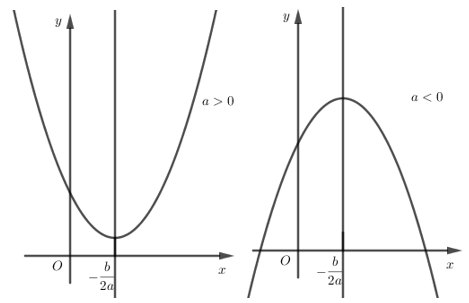
Khi \(a > 0\) đồ thị hàm số bậc hai bề lõm hướng lên trên và có tọa độ đỉnh là \(I\left( { - \dfrac{b}{{2a}}; - \dfrac{\Delta }{{4a}}} \right)\)
Khi \(a < 0\) đồ thị hàm số bậc hai bề lõm hướng xuống dưới và có tọa độ đỉnh là \(I\left( { - \dfrac{b}{{2a}}; - \dfrac{\Delta }{{4a}}} \right)\)
Đồ thị nhận đường thẳng \(x = - \dfrac{b}{{2a}}\) làm trục đối xứng.