1. Định nghĩa
a) Góc giữa hai vectơ
Cho hai vectơ →a và →b đều khác →0. Khi đó:
Góc giữa hai véc tơ →a,→b, kí hiệu (→a;→b) và (→a;→b)=(→OA,→OB)=^AOB.
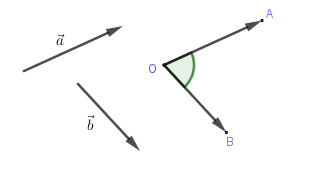
Quy ước: Nếu →a=→0 hoặc →b=→0 thì ta xem góc giữa hai vectơ →a và →b là tùy ý (từ 00 đến 1800).
Ví dụ 1: Cho tam giác ABC vuông cân tại A. Tính góc giữa hai véc tơ:
a. →BA và →BC
b. →CA và →BC
Giải:
Vì tam giác ABC vuông cân nên góc A bằng 900 và góc B bằng góc C bằng 450.
a. Ta có: (→BA,→BC)=^ABC=450
b. Dựng véc tơ →CD=→BC thì (→CA,→BC)=(→CA,→CD)=^ACD=1350
b) Tích vô hướng của hai vectơ
Tích vô hướng của hai véc tơ →a và →b là một số thực được xác định bởi: →a.→b=|→a||→b|.cos(→a,→b).
Ví dụ 2: Với các giả thiết ở ví dụ 1 và cho thêm AB=AC=1, tính →BA.→BC.
Giải:
Ta có: →BA.→BC=|→BA|.|→BC|.cos(→BA,→BC)
Mà |→BA|=BA=1, |→BC|=BC=√AB2+AC2=√2, (→BA,→BC)=^ABC=450 nên:
→BA.→BC=1.√2.cos450=√2.√22=1.
Vậy →BA.→BC=1
2. Tính chất
Với ba véc tơ bất kì →a,→b,→c và mọi số thực k ta luôn có:
1)→a.→b=→b.→a2)→a(→b±→c)=→a.→b±→a.→c3)(k→a)→b=k(→a.→b)=→a(k→b)4)→a2≥0,→a2=0⇔→a=→0
Ta có kết quả sau:
+ Nếu hai véc tơ →a và →b khác →0 thì →a⊥→b⇔→a.→b=0
+ →a.→a=→a2=|→a|2 gọi là bình phương vô hướng của véc tơ →a.
+ (→a±→b)2=→a2±2→a.→b+→b2, (→a+→b)(→a−→b)=→a2−→b2

