Chúng tôi giới thiệu Giải sách bài tập Vật Lí lớp 12 Bài 3: Con lắc đơn chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Vật Lí 12. Mời các bạn đón xem:
Bài giảng Vật Lí 12 Bài 3: Con lắc đơn
Giải SBT Vật Lí 12 Bài 3: Con lắc đơn
Bài 3.1 trang 9 SBT Vật Lí 12: Kéo lệch con lắc đơn ra khỏi vị trí cân bằng một góc rồi buông ra không vận tốc đầu. Chuyển động của con lắc đơn có thể coi như dao động điều hoà khi nào ?
A. Khi .
B. Khi .
C. Khi .
D. Khi Khi nhỏ sao cho
Phương pháp giải:
Sử dụng điều kiện để con lắc đơn dao động điều hòa
Lời giải:
Điều kiện để con lắc đơn dao động điều hòa là nhỏ sao cho
Chọn D
Bài 3.2 trang 9 SBT Vật Lí 12: Một con lắc đơn dao động với biên độ góc nhỏ . Chu kì dao động của nó được tính bằng công thức nào?
A.
B.
C.
D.
Phương pháp giải:
Sử dụng công thức tính chu kì dao động của con lắc đơn:
Lời giải:
Chu kì dao động của con lắc đơn:
Chọn B
Bài 3.3 trang 9 SBT Vật Lí 12: Một con lắc đơn dao động với biên độ góc nhỏ . Câu nào sau đây là sai đối với chu kì của con lắc?
A. Chu kì phụ thuộc chiều dài của con lắc.
B. Chu kì phụ thuộc vào gia tốc trọng trường nơi có con lắc.
C. Chu kì phụ thuộc vào biên độ dao động.
D. Chu kì không phụ thuộc vào khối lượng của con lắc.
Phương pháp giải:
Sử dụng công thức tính chu kì dao động của con lắc đơn:
Lời giải:
Chu kì dao động của con lắc đơn:
Chu kì con lắc đơn chỉ phụ thuộc vào chiều dài con lắc và gia tốc trọng trường tại nơi treo con lắc, không phụ thuộc vào khối lượng và biên độ dao động.
Chọn C
Bài 3.4 trang 9 SBT Vật Lí 12: Tại cùng một nơi trên mặt đất, nếu chu kì dao động điều hoà của con lắc đơn chiều dài là thì chu kì dao động điều hoà của con lắc đơn chiều dài là
A.. B. .
C. . D. .
Phương pháp giải:
Sử dụng công thức tính chu kì dao động của con lắc đơn:
Lời giải:
Chu kì dao động của con lắc đơn:
Chọn A
Bài 3.5 trang 10 SBT Vật Lí 12: Một con lắc đơn dao động điều hoà với biên độ góc . Tại li độ góc bằng bao nhiêu thì thế năng của con lắc bằng nửa động năng của con lắc ?
A. B..
C.. D.
Phương pháp giải:
Sử dụng công thức tính thế năng con lắc đơn:
Sử dụng công thức tính động năng con lắc đơn:
Lời giải:
Ta có:
Lại có
Khi nhỏ:
Chọn C
Bài 3.6 trang 10 SBT Vật Lí 12: Tại một nơi có gia tốc trọng trường , một con lắc đơn và một con lắc lò xo nằm ngang dao động điều hoà với cùng chu kì. Biết con lắc đơn có chiều dài và lò xo có độ cứng . Vật nhỏ của con lắc lò xo có khối lượng là
A. . B. .
C. . D. .
Phương pháp giải:
Sử dụng công thức tính chu kì con lắc đơn:
Sử dụng công thức tính chu kì con lắc lò xo:
Lời giải:
Ta có:
+ Chu kì con lắc đơn:
+ Chu kì con lắc lò xo:
Hai con lắc có cùng chu kì
Chọn B
Bài 3.7 trang 10 SBT Vật Lí 12: Một con lắc đơn dao đồng với biên độ góc nhỏ . Chọn mốc thế năng ở vị trí cân bằng. Công thức tính thế năng của con lắc ở li độ góc nào sau đây là sai?
A.
B.
C.
D.
Phương pháp giải:
Sử dụng công thức tính thế năng con lắc đơn:
Sử dụng công thức lượng giác:
Sử dụng công thức gần đúng: Khi nhỏ
Lời giải:
Ta có thế năng của con lắc đơn
Vì
Khi nhỏ
Chọn B
Bài 3.8 trang 10 SBT Vật Lí 12: Một con lắc đơn dao động với biên độ góc . Chọn mốc thế năng ở vị trí cân bằng. Công thức tính cơ năng nào sau đây là sai ?
A.
B.
C.
D.
Phương pháp giải:
Sử dụng công thức tính động năng:
Sử dụng công thức tính thế năng:
Cơ năng:
Lời giải:
Ta có:
Động năng của con lắc:
Thế năng của con lắc:
+ Cơ năng con lắc:
đúng
+ đúng
+ đúng
Chọn D
Bài 3.9 trang 10 SBT Vật Lí 12: Một con lắc đơn được thả không vận tốc đầu từ vị trí biên có biên độ góc . Khi con lắc đi qua vị trí có li độ góc thì tốc độ của con lắc được tính bằng cồng thức nào? Bỏ qua mọi ma sát
A.
B.
C.
D. .
Phương pháp giải:
Sử dụng công thức tính động năng và rút ra công thức tính vận tốc.
Lời giải:
Ta có:
Chọn A
Bài 3.10 trang 10 SBT Vật Lí 12: Một con lắc gõ giây (coi như một con lắc đơn) có chu kì là . Tại nơi có gia tốc trọng trường là thì chiều dài của con lắc đơn đó là bao nhiêu ?
A. . B. .
C. . D. .
Phương pháp giải:
Sử dụng công thức tính chu kì dao động của con lắc đơn:
Lời giải:
Chu kì dao động của con lắc đơn:
Chọn C
Bài 3.11 trang 10 SBT Vật Lí 12: Một con lắc đơn dài dao động tại một nơi có gia tốc rơi tự do . Kéo con lắc ra khỏi vị trí cân bằng theo chiều dương một góc rồi thả tay.
a) Tính chu kì dao động của con lắc
b) Viết phương trình dao động của con lắc.
c) Tính tốc độ và gia tốc của quả cầu con lắc khi nó đi qua vị trí cân bằng.
Phương pháp giải:
a) Sử dụng công thức tính chu kì con lắc:
b) Vận dụng các bước viết phương trình dao động điều hòa: tìm , tìm , tìm pha ban đầu
c) Sử dụng công thức tính vận tốc và gia tốc.
Lời giải:
a) Chu kì con lắc:
b) Viết phương trình dao động:
+Tần số góc
+ Biên độ
+ Pha ban đầu
Vậy phương trình dao động điều hòa:
c) Tại vị trí cân bằng:
+ Tốc độ:
+ Gia tốc:
Mà:
Chú ý:
Gia tốc con lắc đơn tổng hợp 2 vecto gia tốc thành phần: gia tốc theo phương tiếp tuyến và gia tốc theo phương hướng tâm
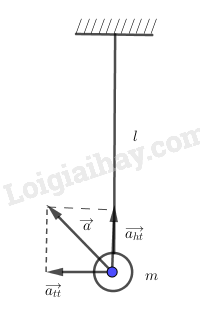
Bài 3.12 trang 10 SBT Vật Lí 12: Một con lắc đơn gồm một quả cầu nhỏ có khối lượng được treo vào đầu một sợi dây dài . Lấy .
a) Tính chu kì dao động của con lắc khi biên độ góc nhỏ.
b) Kéo con lắc ra khỏi vị trí cân bằng đến vị trí có li độ góc rồi buông ra không vận tốc đầu. Tính tốc độ của quả cầu và lực căng của dây khi con lắc đi qua vị trí cân bằng.
Phương pháp giải:
a) Sử dụng công thức tính chu kì con lắc:
b) Sử dụng công thức tính vận tốc và biểu thức định luật II Niuton tính lực căng dây
Lời giải:
Kéo con lắc ra khỏi vị trí cân bằng đến vị trí có li độ góc rồi buông ra không vận tốc đầu
Biên độ góc
a) Chu kì con lắc đơn:
b) Ta có công thức tính động năng
Áp dụng định luật II Niuton:

Chiếu theo phương hướng tâm:
Bài 3.13 trang 11 SBT Vật Lí 12: Một con lắc đơn có chiều dài dao động điều hòa tại một nơi có gia tốc trọng trường là . Trong khi dao động, quả cầu con lắc vạch một cung tròn có độ dài . Bỏ qua ma sát.
a) Tính biên độ và chu kì dao dộng của con lắc.
b) Viết phương trình dao động, biết rằng lúc đầu quả cầu con lắc đi qua vị trí cân bằng theo chiều dương.
c) Tính tốc độ cực đại của quả cầu.
Phương pháp giải:
a) Sử dụng công thức độ dài cung tròn mà con lắc vạch ra trong quá trình dao động
Sử dụng công thức tính chu kì dao động:
b) Vận dụng các bước viết phương trình dao động điều hòa: tìm , tìm , tìm pha ban đầu
c) Sử dụng công thức tính tốc độ cực đại:
Lời giải:
a) Độ dài cung tròn mà con lắc vạch ra trong quá trình dao động
Chu kì dao động:
b) Viết phương trình dao động:
+Tần số góc
+ Biên độ
+ Pha ban đầu
Vậy phương trình dao động điều hòa:
c) Tốc độ cực đại của quả cầu:
Bài 3.14 trang 11 SBT Vật Lí 12: Một con lắc đơn gồm một quả cầu nhỏ, khối lượng treo vào đầu tự do của một sợi dây mảnh dài ở một nơi có gia tốc trọng trường. Bỏ qua ma sát.
a) Cho con lắc dao động với biên độ nhỏ. Tính chu kì dao động của con lắc.
b) Kéo con lắc ra khỏi vị trí cân bằng tới góc lệch rồi thả không vận tốc đầu. Hãy tính:
+ Tốc độ cực đại của quả cầu
+ Tốc độ của quả cầu tại vị trí li độ góc .
Phương pháp giải:
a) Sử dụng công thức tính chu kì dao động:
b) Sử dụng công thức tính tốc độ:
Lời giải:
a) Chu kì dao động:
b) Ta có công thức tính động năng
+ Tốc độ cực đại của quả cầu:
Tại :
Bài 3.15 trang 11 SBT Vật Lí 12: Một con lắc đơn dài . Phía dưới điểm treo , trên phương thẳng đứng có một chiếc đinh đóng chắc vào điểm cách một đoạn , sao cho con lắc vấp vào đinh khi dao động (H.3.1). Kéo con lắc lệch khỏi phương thẳng đứng một góc rồi thả không vận tốc đầu. Bỏ qua ma sát. Hãy tính:
a) Biên độ của con lắc ở hai bên vị trí cân bằng.
b) Chu kì dao động của con lắc. Lấy .
Phương pháp giải:
a) Sử dụng định luật bảo toàn cơ năng.
b) Sử dụng biểu thức xác định chu kì dao động:
Lời giải:
a) Theo định luật bảo toàn cơ năng, ta suy ra hai vị trí biên và phải ở cùng một độ cao (Hình
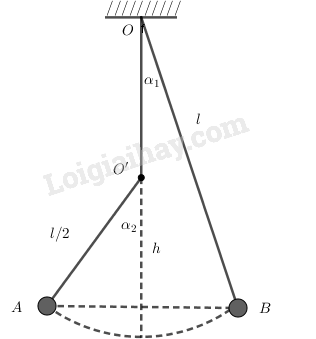
b)

