Giải Vật Lí 12 Bài 14: Mạch có R, L, C mắc nối tiếp

71 lượt xem

Bài trước

Bài sau

Chúng tôi giới thiệu Giải bài tập Vật Lí lớp 12 Bài 14: Mạch có R, L, C mắc nối tiếp chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Mạch có R, L, C mắc nối tiếp lớp 12.

Bài giảng Vật Lí 12 Bài 14: Mạch R,L,C mắc nối tiếp

Giải bài tập Vật Lí Lớp 12 Bài 14: Mạch có R, L, C mắc nối tiếp

Trả lời câu hỏi giữa bài

Trả lời câu C1 trang 75 SGK Vật Lí 12: Hãy nhắc lại định luật về hiệu điện thế trong mạch điện một chiều gồm nhiều điện trở mắc nối tiếp

Lời giải:

Hiệu điện thế của mạch điện một chiều gồm nhiều điện trở ghép nối tiếp bằng tổng hiệu điện thế của từng đoạn U = U1 + U2 + …

Trả lời câu C2 trang 76 SGK Vật Lí 12: Hãy giải thích vị trí tương hỗ của các vecto quay U và I trong hình 14.2 SGK.

Lời giải:

Đoạn mạch chỉ có $\vec{R}$

$\vec{U_{R}}$ hợp với $\vec{I}$ một góc 0o

$\vec{U_{R}}$ song song với $\vec{I}$

Đoạn mạch có C

$\vec{U_{C}}$ hợp với $\vec{I}$ một góc -90o

$\vec{U_{C}}$ vuông góc với $\vec{I}$ hướng xuống

Đoạn mạch chỉ có $\vec{L}$

$\vec{U_{L}}$ hợp với $\vec{I}$ một góc 90o

$\vec{U_{L}}$ vuông góc với $\vec{I}$ hướng lên

Trả lời câu C3 trang 77 SGK Vật Lí 12: Chứng minh các hệ thức (14.1), (14.2) cho trường hợp UL > UC.

Lời giải:

Với $U_{L} > U_{C}$

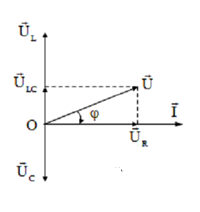
Giải Vật Lí 12 Bài 14: Mạch có R, L, C mắc nối tiếp (ảnh 1)

Từ hình vẽ ta có:

$\begin{aligned} U^{2} = U_{R^{2}} + U_{L C}^{2} = U_{R^{2}} {(U_{L} - U_{C})}^{2} \\ H a y U^{2} = [R^{2} + {(Z_{L} - Z_{C})}^{2}] I^{2} \\ \Rightarrow I = \frac{U}{\sqrt{R^{2} + {(Z_{L} - Z_{C})}^{2}}} \end{aligned}$

Đặt $Z = \sqrt{R^{2} + {(Z_{L} - Z_{C})}^{2}}$

$I = \frac{U}{Z}$

Câu hỏi và bài tập (trang 79 SGK Vật Lí 12)

Bài 1 trang 79 SGK Vật Lí 12: Phát biểu định luật Ôm đối với mạch điện xoay chiều có R, L, C mắc nối tiếp.

Lời giải:

Định luật Ôm của dòng điện xoay chiều của đoạn mạch R, L, C mắc nối tiếp: “Cường độ hiệu dụng trong mạch R, L, C mắc nối tiếp có giá trị bằng thương số của điện áp hiệu dụng giữa hai đầu mạch và tổng trở của mạch.”

Biểu thức: $I = \frac{U}{Z} = \frac{U}{\sqrt{R^{2} + {(Z_{L} - Z_{C})}^{2}}}$

Bài 2 trang 79 SGK Vật Lí 12: Dòng nào ở cột A tương ứng với dòng nào ở cột B ?

Giải Vật Lí 12 Bài 14: Mạch có R, L, C mắc nối tiếp (ảnh 2)

Lời giải:

1 - e; 2 - c; 3 - a;

4 - a; 5 - c; 6 - f.

Bài 3 trang 79 SGK Vật Lí 12: Trong mạch điện xoay chiều nối tiếp, cộng hưởng là gì ? Đặc trưng của cộng hưởng là gì ?

Phương pháp giải:

Sử dụng lí thuyết về hiện tượng cộng hưởng

(SGK trang 78)

Lời giải:

Trong mạch điện xoay chiều nối tiếp, cộng hưởng là hiện tượng cường độ dòng điện trong mạch đạt giá trị lớn nhất khi cảm kháng bằng dung kháng (ZL = Zc).

Đặc trưng của cộng hưởng:

- Dòng điện cùng pha với điện áp.

- Tổng trở mạch đạt giá trị nhỏ nhất là $Z_{m i n} = R$ .

- Cường độ dòng điện có giá trị lớn nhất: $I_{m a x} = \frac{U}{R}$

- Công suất của mạch cực đại: $P_{m a x} = \frac{U^{2}}{R}$

Bài 4 trang 79 SGK Vật Lí 12: Mạch điện xoay chiều gồm có R = 20 Ω nối tiếp với tụ điện C =

\frac{1}{2000 π} F

. Tìm biểu thức của cường độ dòng điện tức thời i, biết u = 60

\sqrt{2}

cos100πt (V).

Phương pháp giải:

Áp dụng công thức tính:

Tổng trở $Z = \sqrt{R^{2} + Z_{C}^{2}}$ ,

Định luật Ohm I = $\frac{U}{Z}$ ,

Công thức tính độ lệch pha giữa u và i tanφ = $\frac{- Z_{C}}{R}$

Của mạch R,C mắc nối tiếp,

Lời giải:

Dung kháng:

$Z_{C} = \frac{1}{ω C} = \frac{1}{100 π \cdot \frac{1}{2000 π}} = 20 Ω$

Tổng trở của mạch là

$Z = \sqrt{R^{2} + Z_{C}^{2}} = \sqrt{20^{2} + 20^{2}}$ $= 20 \sqrt{2} Ω$

Cường độ dòng điện hiệu dụng: $I = \frac{U}{Z} = \frac{60}{20 \sqrt{2}} = \frac{3}{\sqrt{2}} A$

=> $I_{0} = I \sqrt{2} = \frac{3}{\sqrt{2}} . \sqrt{2} = 3 (A)$

Độ lệch pha:

$\tan φ = \frac{- Z_{C}}{R} = - 1 \Rightarrow φ = \frac{- π}{4}$ .

Ta có:

$φ = φ_{u} - φ_{i} \to φ_{i} = φ_{u} - φ = 0 - (- \frac{π}{4}) = \frac{π}{4}$

Tức là i sớm pha hơn u một góc $\frac{π}{4}$

Vậy biểu thức tức thời của cường độ dòng điện là: $i = 3 \cos (100 π t + \frac{π}{4}) (A)$ .

Bài 5 trang 79 SGK Vật Lí 12: Mạch điện xoay chiều gồm có R = 30 Ω nối tiếp với cuộn cảm thuần: L =

\frac{0, 3}{π} H

. Cho điện áp tức thời giữa hai đầu mạch u = 120

\sqrt{2}

cos100πt (V). Viết công thức của i.

Phương pháp giải:

+ Đọc phương trình điện áp

+ Sử dụng biểu thức tính cảm kháng: $Z_{L} = ω L$

+ Sử dụng biểu thức tính tổng trở của mạch: $Z = \sqrt{R^{2} + {(Z_{L} - Z_{C})}^{2}}$

+ Sử dụng biểu thức tính cường độ dòng điện cực đại: $I_{0} = \frac{U_{0}}{Z}$

+ Sử dụng biểu thức tính độ lệch pha của điện áp so với cường độ đòng điện: $\tan φ = \frac{Z_{L} - Z_{C}}{R}$

+ Viết phương trình cường độ dòng điện

Lời giải:

+ Từ phương trình điện áp: $u = 120 \sqrt{2} c o s 100 π t (V)$ , ta có:

- Hiệu điện thế cực đại $U_{0} = 120 \sqrt{2} (V)$

- Tần số góc $ω = 100 π (r a d / s)$

- Pha ban đầu của điện áp: $φ_{u} = 0 (r a d)$

+ Cảm kháng: $Z_{L} = ω L = 100 π . \frac{0, 3}{π} = 30 Ω$

+ Mạch gồm điện trở mắc nối tiếp với cuộn cảm thuần

=> Tổng trở của mạch: $Z = \sqrt{R^{2} + Z_{L}^{2}} = \sqrt{30^{2} + 30^{2}} = 30 \sqrt{2} Ω$

+ Cường độ dòng điện cực đại trong mạch: $I_{0} = \frac{U_{0}}{Z} = \frac{120 \sqrt{2}}{30 \sqrt{2}} = 4 A$

+ Độ lệch pha của u so với i:

$\begin{array}{l} \tan φ = \frac{Z_{L}}{R} = \frac{30}{30} = 1 \\ \Rightarrow φ = \frac{π}{4} (r a d) \end{array}$

Ta có, $φ = \frac{π}{4} > 0$ tức là u nhanh pha hơn i một góc $\frac{π}{4}$

Ta suy ra:

$\begin{array}{l} φ_{u} - φ_{i} = \frac{π}{4} \\ \Rightarrow φ_{i} = φ_{u} - \frac{π}{4} = 0 - \frac{π}{4} = - \frac{π}{4} (r a d) \end{array}$

=> Biểu thức cường độ dòng điện trong mạch: $i = 4 c o s (100 π t - \frac{π}{4}) A$ .

Bài 6 trang 79 SGK Vật Lí 12: Mạch điện xoay chiều gồm điện trở R = 30 Ω nối tiếp với một tụ điện C. Cho biết điện áp hiệu dụng giữa hai đầu mạch bằng 100 V, giữa hai đầu tụ điện bằng 80 V, tính ZC và cường độ hiệu dụng I.

Phương pháp giải:

Áp dụng công thức tính hiệu điện thế hiệu dụng giữa hai đầu đoạn mạch R,C mắc nối tiếp : U2 = U2R + U2C

Cường độ dòng điện hiệu dụng: I = $\frac{U_{R}}{R}$

Lời giải:

Mạch R nối tiếp với C nên UR và UC vuông góc với nhau.

Ta có:

U2 = U2R + U2C =>UR = $\sqrt{U^{2} - U_{C}^{2}}$ = $\sqrt{100^{2} - 80^{2}}$ = 60 V.

Cường độ dòng điện hiệu dụng: I = $\frac{U_{R}}{R}$ = $\frac{60}{30}$ = 2 A.

Dung kháng: ZC = $\frac{U_{C}}{I}$ = $\frac{80}{2}$ = 40 Ω

Bài 7 trang 79 SGK Vật Lí 12: Mạch điện xoay chiều gồm điện trở R = 40 Ω ghép nối tiếp với cuộn cảm thuần L. Cho biết điện áp tức thời hai đầu mạch u = 80cos100πt (V) và điện áp hiệu dụng hai đầu cuộn cảm UL = 40 V.

a) Xác định ZL .

b) Viết công thức của i.

Phương pháp giải:

+ Đọc phương trình điện áp

+ Sử dụng biểu thức tính hiệu điện thế hiệu dụng: $U = \frac{U_{0}}{\sqrt{2}}$

+ Sử dụng biểu thức tính hiệu điện thế hiệu dụng của toàn mạch: $U = \sqrt{U_{R}^{2} + {(U_{L} - U_{C})}^{2}}$

+ Sử dụng biểu thức tính cường độ dòng điện: $I = \frac{U}{Z}$

+ Sử dụng biểu thức tính cảm kháng: $Z_{L} = \frac{U_{L}}{I}$

+ Sử dụng biểu thức tính độ lệch pha của u so với i: $\tan φ = \frac{Z_{L} - Z_{C}}{R} = \frac{U_{L} - U_{C}}{U_{R}}$

+ Viết phương trình cường độ dòng điện trong mạch

Lời giải:

+ Từ phương trình điện áp, $u = 80 c o s 100 π t (V)$ ta có:

- Hiệu điện thế hiệu dụng: $U = \frac{U_{0}}{\sqrt{2}} = \frac{80}{\sqrt{2}} = 40 \sqrt{2} V$

- Tần số góc: $ω = 100 π (r a d / s)$ , $φ_{u} = 0 (r a d)$

+ Mặt khác, hiệu điện thế hiệu dụng giữa hai đầu mạch: $U = \sqrt{U_{R}^{2} + U_{L}^{2}}$

Ta suy ra: $U_{R} = \sqrt{U^{2} - U_{L}^{2}} = \sqrt{{(40 \sqrt{2})}^{2} - 40^{2}} = 40 V$

+ Cường độ dòng điện hiệu dụng trong mạch: $I = \frac{U_{R}}{R} = \frac{40}{40} = 1 A$

=> Cường độ dòng điện cực đại trong mạch: $I_{0} = I \sqrt{2} = 1. \sqrt{2} = \sqrt{2} A$

a) Cảm kháng: $Z_{L} = \frac{U_{L}}{I} = \frac{40}{1} = 40 Ω$

b) Độ lệch pha của u so với i:

$\begin{array}{l} \tan φ = \frac{Z_{L}}{R} = \frac{U_{L}}{U_{R}} = \frac{40}{40} = 1 \\ \Rightarrow φ = \frac{π}{4} (r a d) \end{array}$

Ta suy ra: $φ_{u} - φ_{i} = \frac{π}{4} \Rightarrow φ_{i} = φ_{u} - \frac{π}{4} = 0 - \frac{π}{4} = - \frac{π}{4} (r a d)$

=> Biểu thức cường độ dòng điện trong mạch: $i = \sqrt{2} c o s (100 π t - \frac{π}{4}) A$

Bài 8 trang 79 SGK Vật Lí 12: Mạch điện xoay chiều gồm có: R = 30 Ω, C =

\frac{1}{5000 π} F

, L =

\frac{0, 2}{π} H

. Biết điện áp tức thời hai đầu mạch u = 120

\sqrt{2}

cos100πt (V). Viết biểu thức của i.

Phương pháp giải:

+ Đọc phương trình điện áp

+ Sử dụng biểu thức tính cảm kháng: $Z_{L} = ω L$

+ Sử dụng biểu thức tính dung kháng: $Z_{C} = \frac{1}{ω C}$

+ Sử dụng biểu thức tính tổng trở: $Z = \sqrt{R^{2} + {(Z_{L} - Z_{C})}^{2}}$

+ Sử dụng biểu thức tính cường độ dòng điện cực đại: $I_{0} = \frac{U_{0}}{Z}$

+ Sử dụng biểu thức tính độ lệch pha của u so với i: $\tan φ = \frac{Z_{L} - Z_{C}}{R}$

+ Viết phương trình cường độ dòng điện

Lời giải:

+ Từ phương trình điện áp: $u = 120 \sqrt{2} c o s 100 π t (V)$ , ta có:

- Hiệu điện thế cực đại: $U_{0} = 120 \sqrt{2} (V)$

- Tần số góc: $ω = 100 π (r a d / s)$

- Pha ban đầu của điện áp: $φ_{u} = 0 (r a d)$

+ Cảm kháng: $Z_{L} = ω L = 100 π . \frac{0, 2}{π} = 20 Ω$

+ Dung kháng: $Z_{C} = \frac{1}{ω C} = \frac{1}{100 π . \frac{1}{5000 π}} = 50 Ω$

+ Tổng trở của mạch: $Z = \sqrt{R^{2} + {(Z_{L} - Z_{C})}^{2}} = \sqrt{30^{2} + {(20 - 50)}^{2}} = 30 \sqrt{2} Ω$

+ Cường độ dòng điện cực đại trong mạch: $I_{0} = \frac{U_{0}}{Z} = \frac{120 \sqrt{2}}{30 \sqrt{2}} = 4 A$

+ Độ lệch pha của u so với i:

$\begin{array}{l} \tan φ = \frac{Z_{L} - Z_{C}}{R} = \frac{20 - 50}{30} = - 1 \\ \Rightarrow φ = - \frac{π}{4} (r a d) \end{array}$

Ta suy ra:

$φ_{u} - φ_{i} = - \frac{π}{4} \Rightarrow φ_{i} = φ_{u} + \frac{π}{4} = 0 + \frac{π}{4} = \frac{π}{4} (r a d)$

=> Biểu thức cường độ dòng điện trong mạch: $i = 4 c o s (100 π t + \frac{π}{4}) A$

Bài 9 trang 79 SGK Vật Lí 12: Mạch điện xoay chiều gồm có: R = 40 Ω,

C = \frac{1}{4000 π} F, L = \frac{0, 1}{π} H

. Biết điện áp tức thời hai đầu mạch u = 120

\sqrt{2}

cos100πt (V).

a) Viết biểu thức của i.

b) Tính UAM (H.14.4).

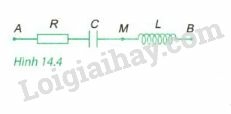
Giải Vật Lí 12 Bài 14: Mạch có R, L, C mắc nối tiếp (ảnh 3)

Phương pháp giải:

Áp dụng công thức tính tổng trở của mạch R,L,C mắc nối tiếp : Z = $\sqrt{R^{2} + (Z_{L} - Z_{C})^{2}}$

Công thức tính độ lệch pha giữa u,i trong mạch xoay chiều tanφ = $\frac{Z_{L} - Z_{C}}{R}$

Định luật Ohm trong mạch điện xoay chiều :I = $\frac{U}{Z}$

Lời giải:

a) Áp dụng các công thức: ZC = $\frac{1}{ω C}$ = 40 Ω; ZL = ωL = 10 Ω

=> Z = $\sqrt{R^{2} + (Z_{L} - Z_{C})^{2}}$ = 50 Ω

Cường độ dòng điện hiệu dụng: I = $\frac{U}{Z}$ = $\frac{120}{50}$ = 2,4A.

Độ lệch pha: tanφ = $\frac{Z_{L} - Z_{C}}{R}$ = $\frac{- 3}{4}$ => φ ≈ -370 ≈ -0,645 rad. Tức là i sớm pha hơn u một góc 0,645 rad.

Vậy biểu thức tức thời của cường độ dòng điện là: i = 2,4 $\sqrt{2}$ cos(100πt + 0,645 ) (A)

b) Tổng trở trên đoạn AM là: $Z_{R C} = \sqrt{R^{2} + Z_{C}^{2}} = \sqrt{40^{2} + 40^{2}} = 40 \sqrt{2} Ω$

UAM có giá trị là UAM = I. ZAM,= 2,4. $40 \sqrt{2}$ = $96 \sqrt{2}$ V

Bài 10 trang 79 SGK Vật Lí 12: Cho mạch điện xoay chiều gồm R = 20 Ω, L =

\frac{0, 2}{π} H

và C =

\frac{1}{2000 π} F

. Biết điện áp tức thời hai đầu mạch u = 80cosωt (V), tính ω để trong mạch có cộng hưởng. Khi đó viết biểu thức của i.

Phương pháp giải:

Áp dụng điều kiện để có cộng hưởng điện ω =

\sqrt{\frac{1}{L C}}

Lời giải:

Hiện tượng cộng hưởng khi:

ZL = ZC⇔ ωL = $\frac{1}{ω C}$ => ω = $\sqrt{\frac{1}{L C}}$ = 100π (rad/s)

Khi đó cường độ dòng điện hiệu dụng đạt giá trị cực đại và dòng điện cùng pha với điện áp:

I = $\frac{U}{R}$ = $\frac{40 \sqrt{2}}{20}$ = 2 $\sqrt{2}$ A => Imax = 4 và φ = 0.

Biểu thức của dòng điện: i = 4cos(100πt) (A).

Bài 11 trang 79 SGK Vật Lí 12: Chọn câu đúng:

Đoạn mạch có R, L, C mắc nối tiếp có R = 40 Ω; $\frac{1}{ω C}$ = 20 Ω; ωL = 60 Ω. Đặt vào hai đầu mạch điện áp u = 240 $\sqrt{2}$ cos100πt (V). Cường độ dòng điện tức thời trong mạch là:

A. i = 3 $\sqrt{2}$ cos100πt (A)

B. i = 6cos(100πt + $\frac{π}{4}$ ) (A)

C. i = 3 $\sqrt{2}$ cos(100πt - $\frac{π}{4}$ ) (A)

D. i = 6cos(100πt - $\frac{π}{4}$ ) (A)

Phương pháp giải:

Áp dụng công thức tính tổng trở của mạch R,L,C mắc nối tiếp : $Z = \sqrt{R^{2} + (Z_{L} - Z_{C})^{2}}$

Công thức tính độ lệch pha giữa u,i trong mạch xoay chiều $t a n φ = \frac{Z_{L} - Z_{C}}{R}$

Định luật Ohm trong mạch điện xoay chiều :

I = \frac{U}{Z}

Lời giải:

Tổng trở của đoạn mạch là $Z = \sqrt{R^{2} + (Z_{L} - Z_{C})^{2}} = 40 \sqrt{2} Ω$

Cường độ dòng điện hiệu dụng: $I = \frac{U}{Z} = \frac{240}{40 \sqrt{2}} = \frac{6}{\sqrt{2}} A$ .

=> Cường độ dòng điện cực đại: $I_{0} = I \sqrt{2} = 6 A$

Độ lệch pha: $t a n φ = \frac{Z_{L} - Z_{C}}{R} = 1 => φ = \frac{π}{4}$ .

Tức là i trễ pha hơn u một góc $\frac{π}{4}$ .

Vậy biểu thức tức thời của cường độ dòng điện là: $i = 6 c o s (100 π t - \frac{π}{4}) A$

Chọn đáp án D

Bài 12 trang 79 SGK Vật Lí 12: Chọn câu đúng:

Đoạn mạch có R, L, C mắc nối tiếp có R = 40 Ω; $\frac{1}{ω C}$ = 30 Ω; ωL = 30 Ω. Đặt vào hai đầu mạch điện áp u = 120 $\sqrt{2}$ cos100πt (V). Biểu thức của dòng điện tức thời trong mạch là:

A. i = 3cos(100πt - $\frac{π}{2}$ ) (A)

B. i = 3 $\sqrt{2}$ (A)

C. i = 3cos100πt (A)

D. i = 3 $\sqrt{2}$ cos100πt (A)

Phương pháp giải:

Áp dụng công thức tính tổng trở của mạch R,L,C mắc nối tiếp : Z = $\sqrt{R^{2} + (Z_{L} - Z_{C})^{2}}$

Công thức tính độ lệch pha giữa u,i trong mạch xoay chiều tanφ = $\frac{Z_{L} - Z_{C}}{R}$

Với $φ = φ_{u} - φ_{i}$

Định luật Ohm trong mạch điện xoay chiều :I = $\frac{U}{Z}$

Lời giải:

Tổng trở của đoạn mạch là Z = $\sqrt{R^{2} + (Z_{L} - Z_{C})^{2}}$ = 40 Ω

Cường độ dòng điện hiệu dụng: I = $\frac{U}{Z}$ = $\frac{120}{40}$ = 3A.

Độ lệch pha: tanφ = $\frac{Z_{L} - Z_{C}}{R}$ = 0 => φ =0. Tức là i và u một góc cùng pha

Vậy biểu thức tức thời của cường độ dòng điện là: i = 3 $\sqrt{2}$ cos(100πt) (A)

Chọn đáp án D.

Phương pháp giải một số dạng bài tập về Mạch xoay chiều có R,L,C mắc nối tiếp

Tổng hợp cách giải một số dạng bài tập về mạch xoay chiều có R,L,C mắc nối tiếp

1. Một số chú ý

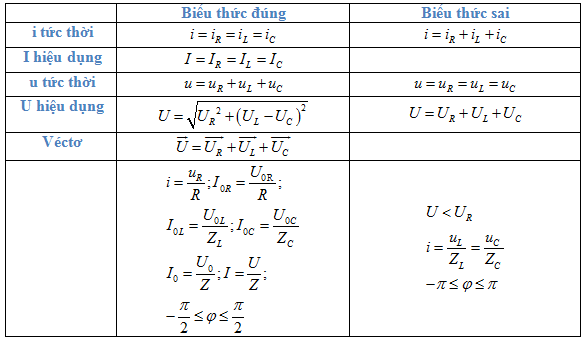
Giải Vật Lí 12 Bài 14: Mạch có R, L, C mắc nối tiếp (ảnh 1)

Đối với mạch chỉ có L, C thì u vuông pha với i

${(\frac{u_{L}}{U_{0 L}})}^{2} + {(\frac{i}{I_{0}})}^{2} = 1$

2. Pha U, I - Viết phương trình U, I

Phương pháp đại số

Bước 1: Xác định các giá trị I0, U0, ω

$U_{0} = I_{0} Z = \sqrt{{U_{0 R}}^{2} + {(U_{0 L} - U_{0 C})}^{2}}$

$Z = \sqrt{R^{2} + {(Z_{L} - Z_{C})}^{2}}$

Bước 2: Xác định pha φu, φi

$\tan φ = \tan (φ_{u} - φ_{i}) = \frac{Z_{L} - Z_{C}}{R}$

$φ > 0 \to φ_{u} > φ_{i}$ : u sớm pha φ so với i (ZL>ZC: mạch có tính cảm kháng)
$φ < 0 \to φ_{u} < φ_{i}$ : u chậm pha φ so với i (ZL

$φ = 0 \to φ_{u} = φ_{i}$ : u cùng pha với i (ZL=ZC: cộng hưởng điện)

Bước 3: Viết phương trình u, i theo đầu bài

Phương pháp vận dụng số phức ( Sử dụng máy tính casio fx570ES)

Cường độ dòng điện: $i = I_{0} c o s (ω t + φ_{i}) \Rightarrow i = I_{0} ∠ φ_{i}$

Điện áp: $u = U_{0} c o s (ω t + φ_{i}) \Rightarrow u = U_{0} ∠ φ_{u}$

Liên hệ giữa u và i: u=i $\bar{Z}$ =i(R+(ZL-ZC) i) - trong đó: i là phần ảo của số phức

Ví dụ 1: Mạch điện xoay chiều gồm một điện trở thuần R=50W, một cuộn thuần cảm có hệ số tự cảm $L = \frac{1}{π} H$ và một tụ điện có điện dung $C = \frac{{2.10}^{- 4}}{π} F$ mắc nối tiếp. Biết rằng dòng điện qua mạch có dạng $i = 5 c o s 100 π t (A)$ . Viết biểu thức điện áp tức thời giữa hai đầu mạch điện.

Cách 1: Phương pháp đại số

Ta có: $R = 50 Ω; Z_{L} = ω L = 100 Ω; Z_{C} = \frac{1}{ω C} = 50 Ω \to Z = \sqrt{R^{2} + {(Z_{L} - Z_{C})}^{2}} = 50 \sqrt{2} Ω$

$U_{0} = I_{0} Z = 5.50 \sqrt{2} = 250 \sqrt{2} V$

$\tan φ = \frac{Z_{L} - Z_{C}}{R} = \frac{100 - 50}{50} = 1 \to φ = \frac{π}{4} \to φ_{u} = φ_{i} + \frac{π}{4}$

$\to u = 250 \sqrt{2} c o s (100 π t + \frac{π}{4}) V$

Cách 2: Phương pháp sử dụng casio

Với máy fx570ES :

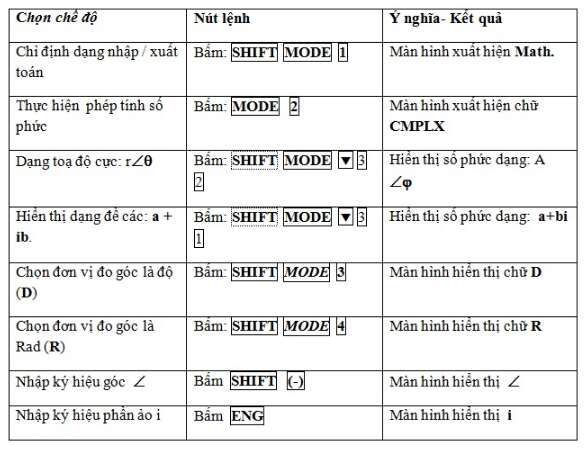
Bước 1: Bấm MODE 2 màn hình xuất hiện: CMPLX.
Bước 2: Bấm SHIFT MODE $\lor$ 3 2 : dạng hiển thị toạ độ cực:( r∠Θ )
Bước 3: Chọn đơn vị đo góc là độ (D) hoặc rad (R) , bấm: SHIFT MODE 3 (hoặc 4 - rad) màn hình hiển thị D hoặc R
Bước 4: Nhập liệu

Ta có: u=i $\bar{Z}$ =I0∠φiX(R+(ZL−ZC))i=5∠0X(50+50i) ( Phép NHÂN hai số phức)

Nhập máy: 5 SHIFT (-) 0 X ( 50 + 50 ENG i )

Bước 5: Gọi kết quả: Shift 2 3 = $353.55339 ∠ 45 = 250 \sqrt{2} ∠ 45$

Vậy biểu thức tức thời điện áp của hai đầu mạch:

$u = 250 \sqrt{2} c o s (100 π t + \frac{π}{4}) V$

Ví dụ 2: Mạch điện xoay chiều gồm một điện trở thuần R=40W, $L = \frac{1}{π} H$ , $C = \frac{10^{- 4}}{0, 6 π} F$ mắc nối tiếp điện áp 2 đầu mạch $u = 100 \sqrt{2} c o s 100 π t (V)$ . Cường độ dòng điện qua mạch là:

Cách 1: Phương pháp đại số

Ta có: $R = 40 Ω; Z_{L} = ω L = 100 Ω; Z_{C} = \frac{1}{ω C} = 60 Ω \to Z = \sqrt{R^{2} + {(Z_{L} - Z_{C})}^{2}} = 40 \sqrt{2} Ω$

$I_{0} = \frac{U_{0}}{Z} = \frac{100 \sqrt{2}}{40 \sqrt{2}} = 2, 5 A$

$\tan φ = \frac{Z_{L} - Z_{C}}{R} = \frac{100 - 40}{40} = 1 \to φ = \frac{π}{4} \to φ_{i} = φ_{u} - \frac{π}{4}$

$\to i = 2, 5 c o s (100 π t - \frac{π}{4}) V$

Cách 2: Phương pháp sử dụng casio

Với máy fx570ES :

Bấm MODE 2 màn hình xuất hiện: CMPLX.
Bấm SHIFT MODE 3 2 : dạng hiển thị toạ độ cực:( r∠Θ )
Chọn đơn vị đo góc là độ (D), bấm: SHIFT MODE 3 màn hình hiển thị D

Ta có: $i = \frac{u}{\bar{Z}} = \frac{U_{0} ∠ φ_{u}}{(R + (Z_{L} - Z_{C}) i)} = \frac{100 \sqrt{2} ∠ 0}{40 + 40 i}$ ( Phép CHIA hai số phức)

Nhập máy: $100 \sqrt{2}$ SHIFT (-) 0 : ( 40 + 40 ENG i ) =

Gọi kết quả: Shift 2 3 = Hiển thị: $2, 5 ∠ - 45$

Vậy biểu thức tức thời điện áp của hai đầu mạch:

$i = 2, 5 c o s (100 π t - \frac{π}{4}) V$

3. Bài toán về cộng hưởng

Điều kiện để có cộng hưởng điện:

$Z_{L} = Z_{C} \Leftrightarrow ω L = \frac{1}{ω C}$ hay $ω^{2} L C = 1$ . Khi đó:

thì ${\begin{cases} Z = Z_{min} = R \\ I = I_{max} = \frac{U}{R} \end{cases}$

$P_{max} = \frac{U^{2}}{R} = I_{max}^{2} . R$

$U_{R} = U; U_{L} = U_{C}; U_{L C} = 0; φ = 0$

u cùng pha với i (cùng pha với uR), u chậm pha $\frac{π}{2}$ so với uL, u nhanh pha $\frac{π}{2}$ so với uC.

Bài tập ví dụ:

Một đoạn mạch gồm $R = 50 Ω$ , cuộn cảm có độ tự cảm L và tụ điện có điện dung $C = \frac{{2.10}^{- 4}}{π} μ F$ mắc nối tiếp. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có điện áp hiệu dụng 110 V, tần số 50 Hz thì thấy u và i cùng pha với nhau. Tính độ tự cảm củam cuộn cảm và công suất tiêu thụ của mạch.

Hướng dẫn giải

Ta có: $Z_{C} = \frac{1}{ω C} = \frac{π}{2 π {.50 .2 .10}^{- 4}} = 50 Ω$

u và i cùng pha => xảy ra cộng hưởng

$Z_{L} = Z_{C} = 50 Ω \Leftrightarrow ω L = 50 \Leftrightarrow L = \frac{50}{2 π .50} = \frac{1}{2 π} H$

Công suất tiêu thụ của mạch:

$P = \frac{U^{2}}{R} = \frac{110^{2}}{50} = 242 W$

Sử dụng giải các bài toán liên quan đến sự lệch pha giữa các điện áp.

4. Bài toán RLC mắc nối tiếp bằng phương pháp giản đồ vecto

a. Cách vẽ giản đồ

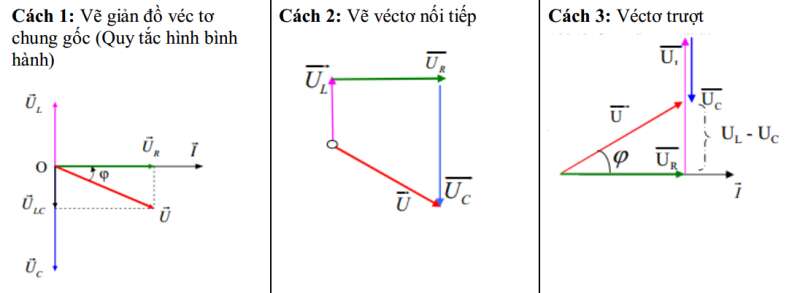
Giải Vật Lí 12 Bài 14: Mạch có R, L, C mắc nối tiếp (ảnh 4)

b. Một số định lí sử dụng trong tam giác thường

Tùy vào từng bài cụ thể, có thể vẽ các véctơ điện áp nối tiếp nhau dựa theo thứ tự của từng mạch điện hoặc vẽ chung gốc. Muốn có mối liên hệ của đại lượng cần tìm và đại lượng đã cho, thường dùng một số liên hệ sau:

- Nếu là tam giác thường:

Định lí hàm số cosin: $a^{2} = b^{2} + c^{2} - 2 b c . c o s A$
Định lí hàm số sin: $\frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC}$

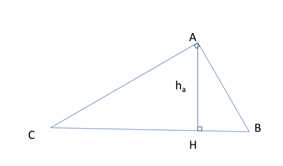
Giải Vật Lí 12 Bài 14: Mạch có R, L, C mắc nối tiếp (ảnh 5)

- Nếu là tam giác vuông:

Định lí hàm sin, cos, tan, cotg
Định lí pitago: $B C^{2} = A B^{2} + A C^{2}$
$\frac{1}{h_{a}^{2}} = \frac{1}{A C^{2}} + \frac{1}{A B^{2}}$
$A H^{2} = H C . H B$
$A C^{2} = C H . C B$
$A C . A B = A H . C B$

c. Ví dụ

Ví dụ: Cho mạch điện xoay chiều như hình vẽ, cuộn dây thuần cảm L, tụ điện có điện dung C, điện trở có giá trị R. Hai đầu A, B duy trì một điện áp $u = 100 \sqrt{2} c o s (100 π t) V$ . Cường độ dòng điện chạy trong mạch có giá trị hiệu dụng là 0,5A. Biết điên áp giữa hai điểm A, M sớm pha hơn dòng điện một góc $\frac{π}{6} r a d$ . Điện áp giữa hai điểm M, B chậm pha hơn điện áp giữa 2 đầu AB một góc $\frac{π}{6} r a d$ .

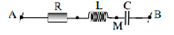
Giải Vật Lí 12 Bài 14: Mạch có R, L, C mắc nối tiếp (ảnh 6)

a. Tìm R, ZC?

b. Viết biểu thức cường độ dòng điện trong mạch?

c. Viết biểu thức điện áp AM?

Lời giải:

Chọn trục dòng điện làm trục pha

Theo bài ra uAM sớm pha $\frac{π}{6}$ so với cường độ dòng điện, uMB chậm pha hơn uAB một góc $\frac{π}{6}$ , mà uMB lại chậm pha so với i một góc $\frac{π}{2}$ nên uAB chậm pha $\frac{π}{3}$ so với dòng điện

=> Ta có giản đồ véctơ:

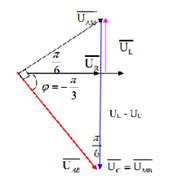
Giải Vật Lí 12 Bài 14: Mạch có R, L, C mắc nối tiếp (ảnh 7)

Từ giản đồ véctơ, ta có:

$U_{A M} = U_{A B} . \tan \frac{π}{6} = \frac{100}{\sqrt{3}} V$

$U_{M B} = U_{C} = U_{A B} . \cos \frac{π}{6} = 100. \frac{\sqrt{3}}{2} = 50 \sqrt{3} V$

$U_{R} = U_{A M} . \cos \frac{π}{6} = 50 V$

a. Ta có: $R = \frac{U_{R}}{I} = \frac{50}{0, 5} = 100 Ω$

$Z_{C} = \frac{U_{C}}{I} = \frac{50 \sqrt{3}}{0, 5} = 100 \sqrt{3}$

b. $I_{0} = 0, 5 \sqrt{2} A$

Độ lệch pha của u so với i: $φ = φ_{u} - φ_{i} = - \frac{π}{3} \to φ_{i} = φ_{u} + \frac{π}{3} = \frac{π}{3}$

=> Biểu thức của i: $i = 0, 5 \sqrt{2} c o s (100 π t + \frac{π}{3}) A$

c. $U_{0 A M} = U_{A M} \sqrt{2} = 100 \sqrt{\frac{2}{3}} V$

Độ lệch pha của uAM so với i : $φ_{A M} - φ_{i} = \frac{π}{6} \to φ_{A M} = \frac{π}{6} + φ_{i} = \frac{π}{6} + \frac{π}{3} = \frac{π}{2}$

=> Biểu thức của uAM: $u_{A M} = 100 \sqrt{\frac{2}{3}} c o s (100 π t + \frac{π}{2}) V$

5. Giải toán RLC xoay chiều bằng phương pháp sử dụng máy tính

a. Sự tương quan giữa điện xoay chiều và số phức

Giải Vật Lí 12 Bài 14: Mạch có R, L, C mắc nối tiếp (ảnh 8)

* Như vậy ta có thể xem R như là một số phức chỉ có phần thực a (vì nằm trên trục hoành), L và C là số phức chỉ có phần ảo b (vì nằm trên trục tung). Nhưng chúng khác nhau là L nằm ở phần dương nên được biểu diễn là bi. C nằm ở phần âm nên được biểu diễn là –bi. u và i được xem như là một số phức x và được viết dưới dạng lượng giác $x = X_{0} ∠ φ$

Giải Vật Lí 12 Bài 14: Mạch có R, L, C mắc nối tiếp (ảnh 9)

b. Các công thức tính toán cơ bản

Khi giải các bài tập điện xoay chiều bằng số phức, ta xem đoạn mạch này như là đoạn mạch một chiều với các phần tử R, L, C mắc nối tiếp.

Chúng ta chỉ sử dụng một định luật duy nhất để giải, đó là định luật Ôm trong mạch điện một chiều.

$I = \frac{U}{R} h a y U = I . R h a y R = \frac{U}{I}$

Trong đó R không chỉ riêng mỗi điện trở mà chỉ chung tất cả những vật có trở kháng (R,ZL, ZC….)

Trong chương trình phổ thông chúng ta chỉ học đoạn mạch xoay chiều mắc nối tiếp cho nên trong đoạn mạch một chiều gồm R1, R2, ……, Rn nối tiếp ta có:

$\begin{matrix} R = R_{1} + R_{2} + \dots \dots + R_{n} \\ U = U_{1} + U_{2} + \dots \dots + U_{n} \\ I = I_{1} = I_{2} = \dots \dots . = I_{n} \end{matrix}$

c. Thao tác trên máy

=> Để thực hiện tính toán số phức trên máy chúng ta phải vào mode CMPLX bằng cách ấn (Mode)(2).

Trên màn hình hiện CMPLX

Trong mode CMPLX:

Để nhập ký hiệu i ta nhấn ENG
Để nhập ký hiệu ngăn cách $∠$ ta nhấn (SHIFT)((-))

Như ta đã biết, số phức có hai cách ghi, đó là đại số và lượng giác

Khi máy tính hiển thị ở dạng đại số (a+bi) thì chúng ta sẽ biết được phần thực và phần ảo của số phức
Khi máy hiển thị ở dạng lượng giác ( $x = X_{0} ∠ φ$ ) thì chúng ta sẽ biết được độ dài (modul) và góc φ (argumen) của số phức.
Mặc định máy tính sẽ hiển thị kết quả dưới dạng đại số. Để chuyển sang dạng lượng giác ta nhấn (SHIFT)(2), chọn (3), nhấn (=). Kết quả sẽ được chuyển sang dạng lượng giác.

d. Những lỗi thường gặp

- Khi cài đặt máy ở chế độ đơn vị đo góc nào thì phải nhập đơn vị đo góc ấy.

Trong mode độ (màn hình hiện lên chữ D), ta phải nhập đơn vị là độ (ví dụ 450, 600, …..)
Trong mode rad (màn hình hiện lên chữ R), ta phải nhập đơn vị là độ (ví dụ π/4, π/3, …..)

- Cách cài đặt máy: Nhấn ((SHIFT)(Mode))

Nhấn (3) cài đặt máy ở đơn vị đo là độ.

Nhấn (4) cài đặt máy ở đơn vị đo là radian.

- Trên máy Fx 570 ES, để bấm nhanh ta thường ấn dấu chia thay cho dấu phân số. Chính vì vậy trong quá trình bấm máy thường xuất hiện những lỗi như sau:

$\begin{array}{l} \frac{1}{2} ∠ \frac{π}{4} k h a c 1 : 2 ∠ \frac{π}{4} \\ \frac{1}{2} ∠ \frac{π}{4} k h a c \frac{1}{2} ∠ π : 4 \\ 3 + 2 i k h a c 3 + (2 i) \end{array}$

- Cách khắc phục: Sử dụng dấu ngoặc

e. Ví d

Ví dụ 1: Khi đặt hiệu điện thế không đổi 30V vào hai đầu đoạn mạch gồm điện trở mắc nối tiếp với cuộn cảm thuần có độ tự cảm $1 / 4 π (H)$ thì dòng điện trong mạch là dòng điện một chiều có cường độ 1A. Nếu đặt vào hai đầu đoạn mạch này điện áp $u = 150 \sqrt{2} c o s 120 π t (V)$ thì biểu thức cường độ dòng điện qua mạch là:

A. $i = 5 \sqrt{2} c o s (120 π t - - \frac{π}{4}) (A)$

B. $i = 5 c o s (120 π t + \frac{π}{4}) (A)$

C. $i = 5 \sqrt{2} c o s (120 π t + \frac{π}{4}) (A)$

D. $i = 5 c o s (120 π t - - \frac{π}{4}) (A)$

Hướng dẫn giải:

Cách giải

Hướng dẫn bấm máy và kết quả

R = U1/I = 30/1 = 30Ω

ω = 120π (rad/s), R = 30Ω, ZL=30Ω, tổng trở phức là Z = 30 + 30i

- Suy ra $i = \frac{U}{Z} = \frac{150 \sqrt{2}}{(30 + 30 i)}$

150√2: (30+30(ENG))= (SHIFT)(2)(3)=

Kết quả: $5 ∠ - \frac{π}{4}$

có nghĩa là i = 5cos(120πt – π/4) (A)

=> Chọn D

Ví dụ 2: Cho mạch điện xoay chiều như hình vẽ

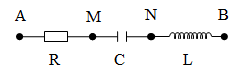
Giải Vật Lí 12 Bài 14: Mạch có R, L, C mắc nối tiếp (ảnh 10)

Có R = 100Ω, L = 0,318H, C = 15,9μF.

Điện áp hai đầu mạch có dạng $u_{A B} = 200 \sqrt{2} c o s (100 π t - 7 π / 12) (V) .$

Viết biểu thức điện áp hai đầu đoạn mạch MB.

A. $u_{M B} = 200 \sqrt{2} c o s (100 π t + 7 π / 12) (V)$

B. $u_{M B} = 200 c o s (100 π t + 7 π / 12) (V)$

C. $u_{M B} = 200 c o s (100 π t - 5 π / 6) (V)$

D. $u_{M B} = 200 c o s (100 π t - 5 π / 12) (V)$

Hướng dẫn giải

Cách giải

Hướng dẫn bấm máy và kết quả

ω = 100π (rad/s), ZC = 200Ω, ZL = 100Ω, R = 100 Ω,

- Tổng trở phức của AB là:

ZAB = 100+100i - 200i

- Tổng trở phức của MB là:

ZMB = 100i - 200i

- $i = \frac{u_{A B}}{Z_{A B}} = \frac{200 \sqrt{2} ∠ - \frac{7 π}{12}}{100 + (100 - 200 i)} =$

- Có i rồi ta suy ra

$u_{M B} = i . Z_{M B} = u_{A B} . \frac{Z_{M B}}{Z_{A B}} = 200 ∠ - \frac{5 π}{6}$

200√2(SHIFT)((-)) $- \frac{7 π}{12}$ :(100+100(ENG)-200(ENG)) = x(100(ENG)-200(ENG)) = (SHIFT)(2)(3)=

Kết quả: $200 ∠ - \frac{5 π}{6}$

$u_{M B} = 200 c o s (100 π t - 5 π / 6) (V)$

6. Bài toán hộp đen

a. Phương pháp đại số

Bước 1: Xác định các thông số có mặt trong hộp đen X

Sử dụng các kiến thức về độ lệch pha giữa các đại lượng tức thời:

+ Khi ux cùng pha với i thì hộp đen X: chỉ chứa R hoặc mạch RLC có cộng hưởng điện.

+ Khi ux nhanh pha hơn i một góc $\frac{π}{2}$ hay i chậm pha hơn ux một góc $\frac{π}{2}$ thì hộp đen X chỉ chứa L hoặc L và C (ZL>ZC)

+ Khi ux chậm pha hơn i một góc $\frac{π}{2}$ hay i nhanh pha hơn ux một góc $\frac{π}{2}$ thì hộp đen X chỉ chứa C hoặc L và C (ZL<ZC)

+ Khi ux nhanh pha hơn i một góc φ (khác 0 và $\frac{π}{2}$ ) thì hộp đen X chứa RL hoặc RLC (ZL>ZC)

+ Khi ux chậm pha hơn i một góc φ (khác 0 và $\frac{π}{2}$ ) thì hộp đen X chứa RC hoặc RLC (ZL<ZC)

+ ...

Bước 2: Xác định các giá trị của các thông số trong hộp đen X

Sử dụng phương pháp đại số hoặc phương pháp giản đồ véctơ.

b. Phương pháp Casio

Dùng máy tính Casio giải bài toán hộp đen

Bài toán cực trị của mạch RLC mắc nối tiếp

CỰC TRỊ CỦA DÒNG ĐIỆN XOAY CHIỀU

I. R thay đổi

1. R THAY ĐỔI ĐỂ PMAX

a. Mạch RLC có cuộn dây thuần cảm (r=0)

$P = U I c o s φ = I^{2} R = \frac{U^{2}}{R^{2} + {(Z_{L} - Z_{C})}^{2}} R = \frac{U^{2}}{R + \frac{{(Z_{L} - Z_{C})}^{2}}{R}}$

Để $P_{m a x} \to {(R + \frac{{(Z_{L} - Z_{C})}^{2}}{R})}_{min}$

Ta có: $R + \frac{{(Z_{L} - Z_{C})}^{2}}{R} \geq 2 \sqrt{R \frac{{(Z_{L} - Z_{C})}^{2}}{R}} = 2 | Z_{L} - Z_{C} |$

Dấu “=” xảy ra $\leftrightarrow R^{2} = (Z_{L} - Z_{C})^{2} \to R = | Z_{L} - Z_{C} |$

b. Mạch RLC có cuộn dây không thuần cảm (r≠0)

- Công suất trên toàn mạch:

$P = I^{2} (R + r) = \frac{U^{2}}{{(R + r)}^{2} + {(Z_{L} - Z_{C})}^{2}} (R + r) = \frac{U^{2}}{R + r + \frac{{(Z_{L} - Z_{C})}^{2}}{R + r}}$

Để $P_{m a x} \to {(R + r + \frac{{(Z_{L} - Z_{C})}^{2}}{R + r})}_{min}$

Ta có: $(R + r) + \frac{{(Z_{L} - Z_{C})}^{2}}{R + r} \geq 2 \sqrt{(R + r) \frac{{(Z_{L} - Z_{C})}^{2}}{R + r}} = 2 | Z_{L} - Z_{C} |$

Dấu “=” xảy ra $\leftrightarrow (R + r)^{2} = (Z_{L} - Z_{C})^{2} \to R + r = | Z_{L} - Z_{C} | \to R = | Z_{L} - Z_{C} | - r$

Chú ý: Nếu $r > Z_{L} - Z_{C} \to P_{m a x} \leftrightarrow R = 0, P_{m a x} = \frac{U^{2}}{r^{2} + {(Z_{L} - Z_{C})}^{2}} r$

- Công suất trên R: $P = \frac{U^{2}}{{(R + r)}^{2} + {(Z_{L} - Z_{C})}^{2}} R = \frac{U^{2}}{R + 2 r + \frac{r^{2} + {(Z_{L} - Z_{C})}^{2}}{R}}$

$\begin{array}{l} A = R + 2 r + \frac{r^{2} + {(Z_{L} - Z_{C})}^{2}}{R} \\ A_{min} \leftrightarrow {(R + \frac{r^{2} + {(Z_{L} - Z_{C})}^{2}}{R})}_{min} \\ R + \frac{r^{2} + {(Z_{L} - Z_{C})}^{2}}{R} \geq 2 \sqrt{R . \frac{r^{2} + {(Z_{L} - Z_{C})}^{2}}{R}} = 2 \sqrt{r^{2} + {(Z_{L} - Z_{C})}^{2}} \end{array}$

Dấu “=” xảy ra: $\leftrightarrow R^{2} = r^{2} + {(Z_{L} - Z_{C})}^{2}, P_{m a x} = \frac{U^{2}}{2 r + 2 \sqrt{r^{2} + {(Z_{L} - Z_{C})}^{2}}}$

- Công suất trên r: $P_{r} = \frac{U^{2} r}{{(R + r)}^{2} + {(Z_{L} - Z_{C})}^{2}}$

$P_{r m a x} = \frac{U^{2} r}{r^{2} + {(Z_{L} - Z_{C})}^{2}}$ xảy ra khi R=0

2. KHI R=R1 HOẶC R=R2 THÌ P CÓ CÙNG 1 GIÁ TRỊ (P<PMAX) (CUỘN DÂY THUẦN CẢM)

$\begin{array}{l} P = \frac{U^{2}}{R^{2} + {(Z_{L} - Z_{C})}^{2}} R \\ \to P (R^{2} + {(Z_{L} - Z_{C})}^{2}) = U^{2} R \\ \leftrightarrow P R^{2} - U^{2} R + {(Z_{L} - Z_{C})}^{2} P = 0 \\ \leftrightarrow R^{2} - \frac{U^{2} R}{P} + {(Z_{L} - Z_{C})}^{2} = 0 (1) \end{array}$

PT (1) có 2 nghiệm: R1, R2 : ${\begin{cases} R_{1} + R_{2} = \frac{U^{2}}{P} \\ R_{1} R_{2} = {(Z_{L} - Z_{C})}^{2} \end{cases}$

II. C thay đổi

1. C THAY ĐỔI => XẢY RA HIỆN TƯỢNG CỘNG HƯỞNG $φ_{U / I} = 0$ VÀ $I_{M A X}, U_{R M A X}, U_{L M A X}, U_{L C M I N}$

$Z_{L} = Z_{C}$

Khi đó:

$\begin{array}{l} Z_{min} = R \\ I_{m a x} = \frac{U}{R} \\ P_{m a x} = I^{2} R = \frac{U^{2}}{R} \end{array}$

+ Điện áp giữa hai đầu điện trở cực đại và bằng điện áp toàn mạch

$U_{L} = U_{C} \to U = \sqrt{U_{R}^{2} + {(U_{L} - U_{C})}^{2}} = U_{R}$

+ Điện áp hai đầu đoạn mạch cùng pha với cường độ dòng điện trong mạch: φ=0

2. C THAY ĐỔI ĐỂ UCMAX VÀ ĐIỆN ÁP HAI ĐẦU ĐOẠN MẠCH VUÔNG PHA VỚI URL

Ta có: $U_{C} = I Z_{C} = \frac{U Z_{C}}{\sqrt{R^{2} + {(Z_{L} - Z_{C})}^{2}}}$

Chia cả tử và mẫu cho ZL, ta được: $U_{C} = \frac{U}{\sqrt{\frac{R^{2}}{{Z_{C}}^{2}} + \frac{{(Z_{L} - Z_{C})}^{2}}{{Z_{C}}^{2}}}} = \frac{U}{\sqrt{\frac{R^{2} + Z_{L}^{2}}{{Z_{C}}^{2}} - \frac{2 Z_{L}}{Z_{C}} + 1}}$

Đặt $y = \frac{R^{2} + Z_{L}^{2}}{{Z_{C}}^{2}} - \frac{2 Z_{L}}{Z_{C}} + 1 = (R^{2} + Z_{L}^{2}) x^{2} - 2 Z_{L} x + 1$ với $x = \frac{1}{Z_{C}}$

Ta có UCmax khi ymin

$y_{min} \leftrightarrow x = - \frac{b}{2 a} = \frac{2 Z_{L}}{2 (R^{2} + Z_{L}^{2})} \to Z_{C} = \frac{R^{2} + Z_{L}^{2}}{Z_{L}}$

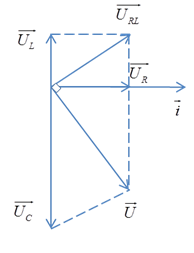
Khi đó: $U_{C m a x} = \frac{U_{R}^{2} + U_{L}^{2}}{U_{L}} = \frac{U \sqrt{R^{2} + Z_{L}^{2}}}{R}$

Hệ quả: ${\begin{cases} U_{R L} ⊥ U_{A B} \\ U_{C max}^{2} = U^{2} + U_{R L}^{2} = U^{2} + U_{R}^{2} + U_{L}^{2} \\ U_{C max}^{} . U_{R} = U . U_{R L} \\ \frac{1}{U_{R}^{2}} = \frac{1}{U^{2}} + \frac{1}{U_{R L}^{2}} \end{cases}$

3. C THAY ĐỔI ĐỂ URCMAX

Ta có: $U_{R C} = I Z_{R C} = \frac{U \sqrt{R^{2} + Z_{C}^{2}}}{\sqrt{R^{2} + {(Z_{L} - Z_{C})}^{2}}} = \frac{U \sqrt{R^{2} + Z_{C}^{2}}}{\sqrt{R^{2} + {Z_{L}}^{2} - 2 Z_{L} Z_{C} + {Z_{C}}^{2}}} = \frac{U}{\sqrt{1 + \frac{- 2 Z_{L} Z_{C} + {Z_{L}}^{2}}{R^{2} + Z_{C}^{2}}}}$

$U_{R L m a x} \leftrightarrow {(1 + \frac{- 2 Z_{L} Z_{C} + {Z_{L}}^{2}}{R^{2} + Z_{C}^{2}})}_{min}$

$\begin{array}{l} y = 1 + \frac{- 2 Z_{L} Z_{C} + {Z_{L}}^{2}}{R^{2} + Z_{C}^{2}} \\ y^{'} = {(1 + \frac{- 2 Z_{L} Z_{C} + {Z_{L}}^{2}}{R^{2} + Z_{C}^{2}})}^{'} = \frac{2 {Z_{C}}^{2} - 2 R^{2} - 2 Z_{L} Z_{C}}{{(R^{2} + Z_{C}^{2})}^{2}} \\ y^{'} = 0 \leftrightarrow 2 {Z_{C}}^{2} - 2 R^{2} - 2 Z_{L} Z_{C} = 0 \\ {\begin{cases} Z_{C} > 0 \\ Z_{C} = \frac{- b + \sqrt{Δ}}{2 a} = \frac{Z_{L} + \sqrt{4 R^{2} + Z_{L}^{2}}}{2} \end{cases} \end{array}$

Khi đó:

$U_{R C max} = \frac{2 U R}{\sqrt{4 R^{2} + Z_{L}^{2}} - Z_{L}}$

4. C THAY ĐỔI ĐỂ URL KHÔNG PHỤ THUỘC VÀO R

URL không phụ thuộc vào R

$\leftrightarrow U_{R L} = U_{A B}$

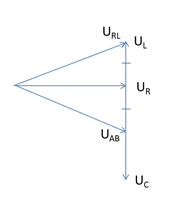
Từ giản đồ:

$\begin{array}{l} \to U_{C} = 2 U_{L} \\ \to Z_{C} = 2 Z_{L} \end{array}$

5. C THAY ĐỔI ĐỂ $U_{R C} ⊥ U_{R L}$

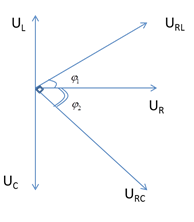
Giải Vật Lí 12 Bài 14: Mạch có R, L, C mắc nối tiếp (ảnh 3)

$\begin{array}{l} U_{R L} ⊥ U_{R C} \\ \leftrightarrow {\begin{cases} \sin φ_{1} = c o s φ_{2} \\ c o s φ_{1} = | \sin φ_{2} | \end{cases} \to | \tan φ_{1} \tan φ_{2} | = 1 \\ \leftrightarrow \frac{U_{L}}{U_{R}} \frac{U_{C}}{U_{R}} = 1 \leftrightarrow U_{L} U_{C} = {U_{R}}^{2} \leftrightarrow Z_{L} Z_{C} = R^{2} \end{array}$

6. C=C1 HOẶC C=C2 THÌ UC CÓ CÙNG GIÁ TRỊ

$C_{1} + C_{2} = 2 C_{m a x} = 2 C_{0} \to C_{0} = \frac{C_{1} + C_{2}}{2}$

7. C THAY ĐỔI CÓ 2 GIÁ TRỊ LÀM CHO: $I_{1} = I_{2}, P_{1} = P_{2}, c o s φ_{1} = c o s φ_{2}, Z_{1} = Z_{2}$

- Z1=Z2

$R^{2} + (Z_{L} - Z_{C 1})^{2} = R^{2} + (Z_{L} - Z_{C 2})^{2} \to | Z_{L} - Z_{C 1} | = | Z_{L} - Z_{C 2} |$

Với ZC2>ZC1 $\to Z_{C 1} + Z_{C 2} = 2 Z_{L}$

- I1=I2 hoặc P1=P2 => L=? để cộng hưởng điện

$\leftrightarrow {\begin{cases} I = I_{m a x} \\ φ_{u} = φ_{i} \\ | c o s φ | = 1 \end{cases} \to 2 Z_{C m a x} = Z_{C 1} + Z_{C 2}$

III. L thay đổi

1- L THAY ĐỔI => XẢY RA HIỆN TƯỢNG CỘNG HƯỞNG $φ_{u / i} = 0$ VÀ IMAX, URMAX, UCMAX, ULCMIN

$Z_{L} = Z_{C}$

Khi đó:

$Z_{min} = R, I_{m a x} = \frac{U}{R}, P_{m a x} = I^{2} R = \frac{U^{2}}{R}$

+ Điện áp giữa hai đầu điện trở cực đại và bằng điện áp toàn mạch

$U_{L} = U_{C} \to U = \sqrt{U_{R}^{2} + {(U_{L} - U_{C})}^{2}} = U_{R}$

+ Điện áp hai đầu đoạn mạch cùng pha với cường độ dòng điện trong mạch: φ=0I

2 - L THAY ĐỔI ĐỂ ULMAX VÀ ĐIỆN ÁP HAI ĐẦU ĐOẠN MẠCH VUÔNG PHA VỚI URC

Ta có: $U_{L} = I Z_{L} = \frac{U Z_{L}}{\sqrt{R^{2} + {(Z_{L} - Z_{C})}^{2}}}$

Chia cả tử và mẫu cho ZL, ta được: $U_{L} = \frac{U}{\sqrt{\frac{R^{2}}{{Z_{L}}^{2}} + \frac{{(Z_{L} - Z_{C})}^{2}}{{Z_{L}}^{2}}}} = \frac{U}{\sqrt{\frac{R^{2} + Z_{C}^{2}}{{Z_{L}}^{2}} - \frac{2 Z_{C}}{Z_{L}} + 1}}$

Đặt $y = \frac{R^{2} + Z_{C}^{2}}{{Z_{L}}^{2}} - \frac{2 Z_{C}}{Z_{L}} + 1 = (R^{2} + Z_{C}^{2}) x^{2} - 2 Z_{C} x + 1$ với $x = \frac{1}{Z_{L}}$

Ta có ULmax khi ymin

$y_{min} \leftrightarrow x = - \frac{b}{2 a} = \frac{2 Z_{C}}{2 (R^{2} + Z_{C}^{2})} \to Z_{L} = \frac{R^{2} + Z_{C}^{2}}{Z_{C}}$

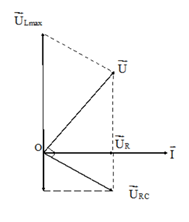
Khi đó: $U_{L m a x} = \frac{U_{R}^{2} + U_{C}^{2}}{U_{C}} = \frac{U \sqrt{R^{2} + Z_{C}^{2}}}{R}$

Hệ quả: ${\begin{cases} U_{R C} ⊥ U_{A B} \\ U_{L max}^{2} = U^{2} + U_{R C}^{2} = U^{2} + U_{R}^{2} + U_{C}^{2} \\ U_{L max}^{} . U_{R} = U . U_{R C} \\ \frac{1}{U_{R}^{2}} = \frac{1}{U^{2}} + \frac{1}{U_{R C}^{2}} \end{cases}$

3 - L THAY ĐỔI ĐỂ URLMAX

Ta có: $U_{R L} = I Z_{R L} = \frac{U \sqrt{R^{2} + Z_{L}^{2}}}{\sqrt{R^{2} + {(Z_{L} - Z_{C})}^{2}}} = \frac{U \sqrt{R^{2} + Z_{L}^{2}}}{\sqrt{R^{2} + {Z_{L}}^{2} - 2 Z_{L} Z_{C} + {Z_{C}}^{2}}} = \frac{U}{\sqrt{1 + \frac{- 2 Z_{L} Z_{C} + {Z_{C}}^{2}}{R^{2} + Z_{L}^{2}}}}$

URLmax $\leftrightarrow {(1 + \frac{- 2 Z_{L} Z_{C} + {Z_{C}}^{2}}{R^{2} + Z_{L}^{2}})}_{min}$

$\begin{aligned} y = 1 + \frac{- 2 Z_{L} Z_{C} + Z_{C}^{2}}{R^{2} + Z_{L}^{2}} \\ y^{'} = {(1 + \frac{- 2 Z_{L} Z_{C} + Z_{C}^{2}}{R^{2} + Z_{L}^{2}})}^{'} = \frac{2 Z_{L}^{2} - 2 R^{2} - 2 Z_{L} Z_{C}}{{(R^{2} + Z_{L}^{2})}^{2}} \\ y^{'} = 0 \leftrightarrow 2 Z_{L}^{2} - 2 R^{2} - 2 Z_{L} Z_{C} = 0 \end{aligned}$

$Z_{L} > 0, Z_{L} = \frac{- b + \sqrt{Δ}}{2 a} = \frac{Z_{C} + \sqrt{4 R^{2} + Z_{C}^{2}}}{2}$

Khi đó:

$U_{R L_{max}} = \frac{2 U R}{\sqrt{4 R^{2} + Z_{C}^{2}} - Z_{C}}$

4 - L THAY ĐỔI ĐỂ URC KHÔNG PHỤ THUỘC VÀO R

URC không phụ thuộc vào R

$\leftrightarrow U_{R C} = U_{A B}$

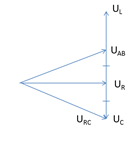
Từ giản đồ:

$\begin{array}{l} \leftrightarrow U_{C} = U_{L} - U_{C} \\ \to U_{L} = 2 U_{C} \\ \to Z_{L} = 2 Z_{C} \end{array}$

5 - L THAY ĐỔI ĐỂ $U_{R C} ⊥ U_{R L}$

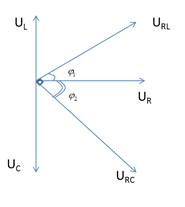
6 - L=L1HOẶC L=L2 THÌ UL CÓ CÙNG GIÁ TRỊ

$\frac{1}{L_{m a x}} = \frac{1}{2} (\frac{1}{L_{1}} + \frac{1}{L_{2}})$

7 - L THAY ĐỔI, CÓ 2 GIÁ TRỊ CỦA L LÀM CHO $I_{1} = I_{2}, P_{1} = P_{2}, c o s φ_{1} = c o s φ_{2}, Z_{1} = Z_{2}$

- Z1=Z2

$R^{2} + (Z_{L 1} - Z_{C})^{2} = R^{2} + (Z_{L 2} - Z_{C})^{2} \to | Z_{L 1} - Z_{C} | = | Z_{L 2} - Z_{C} |$

Với ZL2>ZL1 $\to Z_{L 1} + Z_{L 2} = 2 Z_{C}$

- I1=I2 hoặc P1=P2 => L=? để cộng hưởng điện

$\leftrightarrow {\begin{cases} I = I_{m a x} \\ φ_{u} = φ_{i} \\ | c o s φ | = 1 \end{cases} \to L = \frac{L_{1} + L_{2}}{2}$

IV. $ω$ thay đổi

1. $ω$ THAY ĐỔI ĐỂ XẢY RA HIỆN TƯỢNG CỘNG HƯỞNG ĐIỆN: $Z_{m i n}, I_{m a x}, U_{R m a x}, P_{A B m a x}, c o s φ$ CỰC ĐẠI

$Z_{L} = Z_{C} \to ω^{2} = \frac{1}{L C} h a y ω = \frac{1}{\sqrt{L C}}$

Khi đó:

$Z_{min} = R, I_{m a x} = \frac{U}{R}, P_{m a x} = I^{2} R = \frac{U^{2}}{R}$

+ Điện áp giữa hai đầu điện trở cực đại và bằng điện áp toàn mạch

$U_{L} = U_{C} \to U = \sqrt{U_{R}^{2} + {(U_{L} - U_{C})}^{2}} = U_{R}$

+ Điện áp hai đầu đoạn mạch cùng pha với cường độ dòng điện trong mạch: $φ = 0$

2. $ω$ THAY ĐỔI ĐỂ UCMAX

$U_{C} = I Z_{C} = \frac{U Z_{C}}{\sqrt{R^{2} + {(Z_{L} - Z_{C})}^{2}}} = \frac{U}{ω C \sqrt{R^{2} + ω^{2} L^{2} - 2 \frac{L}{C} + \frac{1}{ω^{2} C^{2}}}} = \frac{U}{C \sqrt{ω^{4} L^{2} + (R^{2} - 2 \frac{L}{C}) ω^{2} + \frac{1}{C^{2}}}}$

UC max <=> mẫu min

Đặt $ω^{2} = x$ , $\to x^{2} L^{2} + (R^{2} - 2 \frac{L}{C}) x + \frac{1}{C^{2}} = y$

$y_{min} \leftrightarrow x = - \frac{b}{2 a} = \frac{1}{L C} - \frac{R^{2}}{2 L^{2}}, y_{min} = - \frac{Δ}{4 a} = \frac{R^{2}}{L C} - \frac{R^{4}}{2 L^{2}}$

Khi đó ta có:

$\begin{array}{l} Z_{L} = ω L = \sqrt{\frac{1}{L C} - \frac{R^{2}}{2 L^{2}}} L \to Z_{L}^{2} = \frac{L}{C} - \frac{R^{2}}{2} \\ \leftrightarrow Z_{L}^{2} = Z_{L} Z_{C} - \frac{R^{2}}{2} \\ \to \frac{R^{2}}{2} = Z_{L} (Z_{C} - Z_{L}) \\ \to \frac{Z_{L}}{R} \frac{(Z_{C} - Z_{L})}{R} = \frac{1}{2} \leftrightarrow \tan φ_{R L} \tan φ = - \frac{1}{2} \end{array}$

Vẽ giản đồ ta được:

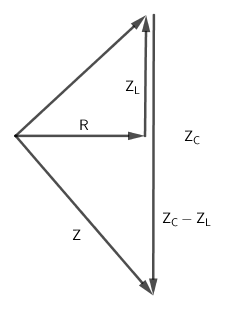
Từ giản đồ, ta có:

$\begin{array}{l} Z^{2} = R^{2} + {(Z_{C} - Z_{L})}^{2} = 2 Z_{L} (Z_{C} - Z_{L}) + {(Z_{C} - Z_{L})}^{2} \\ \leftrightarrow Z^{2} = Z_{C}^{2} - Z_{L}^{2} \end{array}$

Kết luận: $ω$ biên thiên để $U_{C_{m a x}}$ , khi đó:

$U_{C m a x} = \frac{2 U L}{R \sqrt{4 L C - R^{2} C^{2}}}, ω^{2} = \frac{1}{L C} - \frac{R^{2}}{2 L^{2}}$

$\tan φ_{R L} \tan φ = - \frac{1}{2}$ và $Z_{C}^{2} = Z^{2} + Z_{L}^{2}$

3. $ω$ THAY ĐỔI ĐỂ ULMAX

$U_{L} = I Z_{L} = \frac{U Z_{L}}{\sqrt{R^{2} + {(Z_{L} - Z_{C})}^{2}}} = \frac{U ω L}{\sqrt{R^{2} + ω^{2} L^{2} - 2 \frac{L}{C} + \frac{1}{ω^{2} C^{2}}}} = \frac{U L}{\sqrt{L^{2} + \frac{(R^{2} - 2 \frac{L}{C})}{ω^{2}} + \frac{1}{ω^{4} C^{2}}}}$

$U_{L m a x}$ <=> mẫu min

Đặt $\frac{1}{ω^{2}} = x$ , $\to L^{2} + (R^{2} - 2 \frac{L}{C}) x + x^{2} \frac{1}{C^{2}} = y$

$y_{min} \leftrightarrow x = - \frac{b}{2 a} = \frac{2 L C - R^{2} C^{2}}{2}, y_{min} = - \frac{Δ}{4 a} = \frac{4 L R^{2} - R^{4} C}{4} C$

Khi đó ta có:

$\begin{array}{l} \to Z_{C}^{2} = \frac{1}{ω^{2} C^{2}} = \frac{1}{\frac{2}{2 L C - R^{2} C^{2}} C^{2}} = \frac{L}{C} - \frac{R^{2}}{2} \\ \leftrightarrow Z_{C}^{2} = Z_{L} Z_{C} - \frac{R^{2}}{2} \\ \leftrightarrow \frac{R^{2}}{2} = Z_{C} (Z_{L} - Z_{C}) \leftrightarrow \frac{Z_{C}}{R} \frac{(Z_{L} - Z_{C})}{R} = \frac{1}{2} \\ \leftrightarrow \tan φ_{R C} \tan φ = - \frac{1}{2} \end{array}$

Vẽ giản đồ ta được:

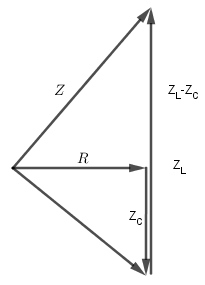
Từ giản đồ, ta có:

$\begin{array}{l} Z^{2} = R^{2} + {(Z_{L} - Z_{C})}^{2} = 2 Z_{C} (Z_{L} - Z_{C}) + {(Z_{C} - Z_{L})}^{2} \\ \leftrightarrow Z^{2} = Z_{L}^{2} - Z_{C}^{2} \end{array}$

Kết luận: $U_{L m a x} = \frac{2 U L}{R \sqrt{4 L C - R^{2} C^{2}}}, ω^{2} = \frac{2}{2 L C - R^{2} C^{2}}$

$\tan φ_{R C} \tan φ = - \frac{1}{2}$ và $Z_{L}^{2} = Z^{2} + Z_{C}^{2}$

*Chú ý:

Khi $ω$ thay đổi để $U_{C m a x}, U_{L m a x}$

$\begin{array}{l} U_{C m a x} = U_{L m a x} = \frac{2 U L}{R \sqrt{4 L C - R^{2} C^{2}}} \\ ω_{L} . ω_{C} = \frac{1}{L C} = ω_{0}^{2} \end{array}$

4. THAY ĐỔI $f$ CÓ HAI GIÁ TRỊ $f_{1} \neq f_{2}$ BIẾT $f_{1} + f_{2} = a$ VÀ CÙNG CÔNG SUẤT HOẶC CÙNG $I, Z, c o s φ, U_{R .}$

- Hai giá trị tần số làm cho mạch có cùng công suất nên:

$\begin{array}{l} P_{1} = P_{2} \Leftrightarrow I_{1}^{2} R = I_{2}^{2} R \Leftrightarrow I_{1}^{2} = I_{2}^{2} \\ \to \frac{U^{2}}{R^{2} + {(Z_{L 1} - Z_{C 1})}^{2}} = \frac{U^{2}}{R^{2} + {(Z_{L 2} - Z_{C 2})}^{2}} \\ \to (Z_{L 1} - Z_{C 1})^{2} = (Z_{L 2} - Z_{C 2})^{2} \to [\begin{array}{l} Z_{L 1} - Z_{C 1} = Z_{L 2} - Z_{C 2} (l o a i) \\ Z_{L 1} - Z_{C 1} = - (Z_{L 2} - Z_{C 2}) \end{array} \\ \to Z_{L 1} + Z_{L 2} = Z_{C 1} + Z_{C 2}) \to L (ω_{1} + ω_{2}) = \frac{1}{C} (\frac{1}{ω_{1}} + \frac{1}{ω_{2}}) = \frac{1}{C} \frac{ω_{1} + ω_{2}}{ω_{1} ω_{2}} \\ \to ω_{1} ω_{2} = \frac{1}{L C} = ω_{0}^{2} \end{array}$

- Công thức trên áp dụng cho bài toán thay đổi f có cùng I, Z, cosφ, UR

Các hệ quả thu được:

Cảm kháng và dung kháng trong hai trường hợp:

$(Z_{L 1} - Z_{C 1})^{2} = (Z_{L 2} - Z_{C 2})^{2} h a y | Z_{L} - Z_{C} | = h / s \to | \begin{array}{l} Z_{L 1} = Z_{C 2} \\ Z_{L 2} = Z_{C 1} \end{array}$

Hệ số công suất trong hai trường hợp: $c o s φ_{1} = c o s φ_{2} = \frac{1}{\sqrt{1 + k {(\sqrt{\frac{ω_{1}}{ω_{2}}} - \sqrt{\frac{ω_{2}}{ω_{1}}})}^{2}}} (\frac{L}{C} = k . R^{2})$
Cường độ dòng điện trong hai trường hợp: $I_{1} = I_{2} = \frac{I_{m a x}}{n}$

Điện trở của mạch được xác định: $R = L \frac{| ω_{1} - ω_{2} |}{\sqrt{n^{2} - 1}} = \frac{| ω_{1} - ω_{2} |}{ω_{1} ω_{2} C \sqrt{n^{2} - 1}}$

Lý thuyết Bài 14: Mạch có R, L, C mắc nối tiếp

Điện áp và tổng trở của mạch:

${\begin{cases} U = \sqrt{U_{R}^{2} + {(U_{L} - U_{C})}^{2}} \to U_{0} = \sqrt{U_{0 R}^{2} + {(U_{0 L} - U_{0 C})}^{2}} \\ Z = \sqrt{R_{}^{2} + {(Z_{L} - Z_{C})}^{2}} \end{cases}$

Định luật Ohm cho mạch:

${\begin{cases} I = \frac{U}{Z} = \frac{\sqrt{U_{R}^{2} + {(U_{L} - U_{C})}^{2}}}{\sqrt{R_{}^{2} + {(Z_{L} - Z_{C})}^{2}}} = \frac{U_{R}}{R} = \frac{U_{L}}{Z_{L}} = \frac{U_{C}}{Z_{C}} = \frac{I_{0}}{\sqrt{2}} \\ I_{0} = \frac{U_{0}}{Z} = \frac{\sqrt{U_{0 R}^{2} + {(U_{0 L} - U_{0 C})}^{2}}}{\sqrt{R_{}^{2} + {(Z_{L} - Z_{C})}^{2}}} = \frac{U_{0 R}}{R} = \frac{U_{0 L}}{Z_{L}} = \frac{U_{0 C}}{Z_{C}} = I \sqrt{2} \end{cases}$

Độ lệch pha của điện áp và cường độ dòng điện trong mạch là $φ$ , được cho bởi: $\tan φ = \frac{U_{L} - U_{C}}{U_{R}} = \frac{Z_{L} - Z_{C}}{R}$ ; $φ = φ_{u} - φ_{i}$

- Khi $U_{L} > U_{C}$ hay $Z_{L} > Z_{C}$ thì u nhanh pha hơn i góc $φ$ . (Hình 1). Khi đó ta nói mạch có tính cảm kháng.

- Khi $U_{L} < U_{C}$ hay $Z_{L} < Z_{C}$ thì u chậm pha hơn i góc $φ$ . (Hình 2). Khi đó ta nói mạch có tính dung kháng.

Giản đồ véc tơ (Giản đồ Frenen):

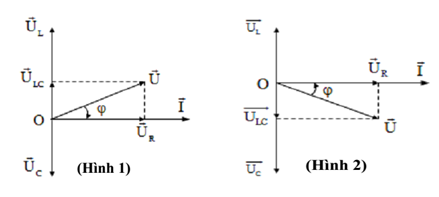
Hiện tượng cộng hưởng

Khi $Z_{L} = Z_{C} \Leftrightarrow ω L = \frac{1}{ω C} \Leftrightarrow ω^{2} L C = 1$ thì $\tan φ = 0 \Rightarrow φ = 0$ suy ta dòng điện i cùng pha với điện áp u.

Khi đó: ${\begin{cases} Z_{min} = R \\ I_{max} = \frac{U}{R} \end{cases}$

=> Đó là hiện tượng cộng hưởng.

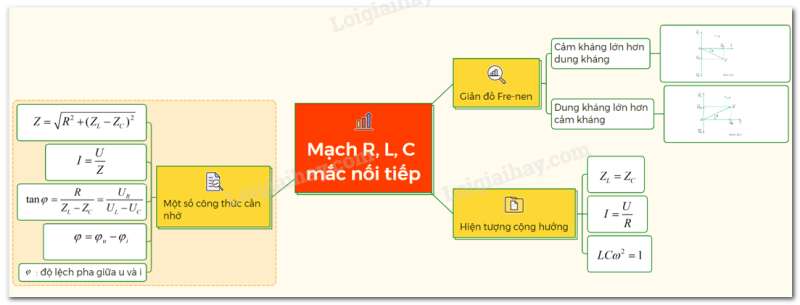
Sơ đồ tư duy về mạch R, L, C mắc nối tiếp

Xem thêm các chương trình khác:

Bài trước

Bài sau

Giải SGK, SBT, Chuyên đề Vật Lý Lớp 12