Giải Vật Lí 12 Bài 20: Mạch dao động

89 lượt xem

Bài trước

Bài sau

Chúng tôi giới thiệu Giải bài tập Vật Lí lớp 12 Bài 20: Mạch dao động chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Mạch dao động lớp 12.

Bài giảng Vật Lí 12 Bài 20: Mạch dao động

Giải bài tập Vật Lí Lớp 12 Bài 20: Mạch dao động

Trả lời câu hỏi giữa bài

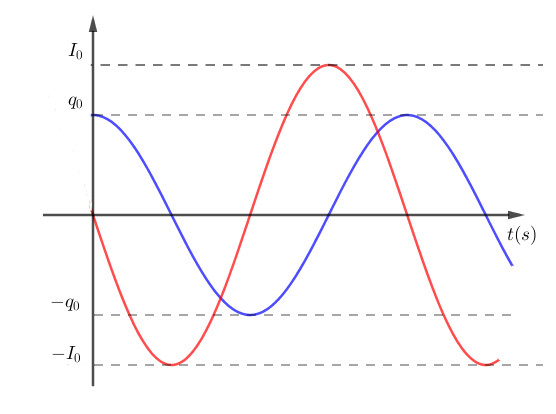
Trả lời câu C1 trang 105 SGK Vật Lí 12: Hãy vẽ đồ thị biểu diễn các hàm số q(t) và i(t) ở các công thức (20.1 SGK) và (20.3 SGK) ứng với φ = 0 trên cùng một hệ trục tọa độ.

Phương pháp giải:

Vẽ đồ thị hàm số cos

Lời giải:

$q = q_{0} \cos ω t$ và $i = I_{0} \cos (ω t + \frac{π}{2})$

$\Leftrightarrow {\begin{matrix} q = q_{0} \cos (\frac{2 π}{T} . t) \\ i = I_{0} \cos (\frac{2 π}{T} + \frac{π}{2}) \end{matrix}$

Vẽ trên đồ thị ta được:

Giải Vật Lí 12 Bài 20: Mạch dao động (ảnh 1)

Câu hỏi và bài tập (trang 107 SGK Vật Lí 12)

Bài 1 trang 107 SGK Vật Lí 12: Mạch dao động là gì?

Lời giải:

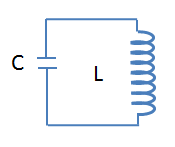
Mạch dao động là mạch gồm tụ điện mắc nối tiếp với một cuộn cảm thành mạch kín.

Giải Vật Lí 12 Bài 20: Mạch dao động (ảnh 2)

Bài 2 trang 107 SGK Vật Lí 12: Nêu định luật biến thiên của điện tích của một bản tụ điện và cường độ dòng điện trong mạch dao động?

Lời giải:

Điện tích của một bản tụ điện và cường độ dòng điện trong mạch dao động biến thiên điều hòa theo thời gian

$q = q_{0} c o s (ω t + φ)$

$i = I_{0} c o s (ω t + φ + \frac{π}{2})$

Trong đó, cường độ dòng điện $i$ sớm pha $\frac{π}{2}$ so với $q$

Bài 3 trang 107 SGK Vật Lí 12: Viết công thức tính chu kỳ và tần số dao động riêng của mạch dao động?

Lời giải:

Ta có, tần số góc của mạch dao động: $ω = \frac{1}{\sqrt{L C}}$

+ Chu kì dao động: $T = \frac{2 π}{ω} = 2 π \sqrt{L C}$

+ Tần số dao động: $f = \frac{1}{T} = \frac{1}{2 π \sqrt{L C}}$

Bài 4 trang 107 SGK Vật Lí 12: Dao động điện từ tự do là gì?

Lời giải:

Dao động điện từ tự do là sự biến thiên điều hòa theo thời gian của điện tích $q$ của một bản tụ điện và cường độ dòng điện $i$ (hoặc cường độ điện trường $\vec{E}$ và cảm ứng từ $\vec{B}$ ) trong mạch dao động.

Bài 5 trang 107 SGK Vật Lí 12: Năng lượng điện từ là gì?

Lời giải:

Năng lượng điện từ là tổng năng lượng điện trường trong tụ điện và năng lượng từ trường trong cuộn cảm của mạch dao động.

$W = W_{d} + W_{t} = \frac{1}{2} C u^{2} + \frac{1}{2} L i^{2}$

Bài 6 trang 107 SGK Vật Lí 12: Sự biến thiên của dòng điện $i$ trong một mạch dao động lệch pha như thế nào so với sự biến thiên của điện tích q của một bản tụ điện?

A. $i$ cùng pha với $q$

B. $i$ ngược pha với $q$

C. $i$ sớm pha so $\frac{π}{2}$ với $q$

D. $i$ trễ pha so $\frac{π}{2}$ với $q$

Phương pháp giải:

Sự biến thiên của điện tích và cường độ dòng điện trong mạch dao động:

+ Điện tích: $q = q_{0} c o s (ω t + φ)$

+ Cường độ dòng điện: $i = I_{0} c o s (ω t + φ + \frac{π}{2})$

Lời giải:

Đáp án C

Ta có:

+ Điện tích: $q = q_{0} c o s (ω t + φ)$

+ Cường độ dòng điện: $i = I_{0} c o s (ω t + φ + \frac{π}{2})$

=> Điện tích và cường độ dòng điện biến thiên điều hòa theo thời gian, cường độ dòng điện $i$ sớm pha $\frac{π}{2}$ so với điện tích $q$

Bài 7 trang 107 SGK Vật Lí 12: Nếu tăng số vòng dây của cuộn cảm thì chu kì của dao động điện từ sẽ thay đổi như thế nào?

A. Tăng.

B .Giảm.

C. Không đổi.

D. Không đủ cơ sở để trả lời .

Phương pháp giải:

+ Vận dụng biểu thức tính hệ số tự cảm: $L = 4 π {.10}^{- 7} n^{2} V = 4 π {.10}^{- 7} \frac{N^{2}}{l} S$

Với n: số vòng dây trên một đơn vị chiều dài của ống (cuộn) $n = \frac{N}{l}$

+ Vận dụng biểu thức tính chu kì dao động: $T = 2 π \sqrt{L C}$

Lời giải:

Đáp án A.

+ Ta có: $L = 4 π {.10}^{- 7} n^{2} V = 4 π {.10}^{- 7} \frac{N^{2}}{l} S$

=> Khi tăng số vòng dây của cuộn cảm thì độ tự cảm L của cuộn dây tăng

+ Lại có, chu kì dao động: $T = 2 π \sqrt{L C}$

=> Khi L tăng thì chu kì dao động T cũng tăng

Vậy, Khi tăng số vòng dây của cuộn cảm thì chu kì dao động điện từ T tăng

Bài 8 trang 107 SGK Vật Lí 12: Tính chu kì và tần số dao động riêng của một mạch dao động, biết tụ điện trong mạch có điện dung là 120pF và cuộn cảm có độ tự cảm là 3mH.

Phương pháp giải:

+ Chu kì dao động riêng của mạch dao động: $T = 2 π \sqrt{L C}$

+ Tần số: f = 1/T

Lời giải:

L = 3mH = 3.10-3 H; C = 120pF = 120.10-12F

+ Chu kì: $T = 2 π \sqrt{L C} = 2 π \sqrt{{3.10}^{- 3} {.120 .10}^{- 12}} = 3, {77.10}^{- 6} s$

+ Tần số: $f = \frac{1}{T} = 0, {265.10}^{6} H z = 0, 265 M H z$

Phương pháp giải một số dạng bài tập về mạch dao động

Tổng hợp cách giải một số dạng bài tập về mạch dao động thường gặp

1. Dạng 1: Xác định chu kì, tần số của mạch dao động

- Tần số góc: $ω = \frac{1}{\sqrt{L C}} \to T = 2 π \sqrt{L C}; f = \frac{1}{2 π \sqrt{L C}}$

Lập tỉ số, ta có: $\frac{T_{1}}{T_{2}} = \frac{f_{2}}{f_{1}} = \frac{ω_{1}}{ω_{2}} = \sqrt{\frac{L_{2}}{L_{1}}} . \sqrt{\frac{C_{2}}{C_{1}}}$
$ω_{0} = \frac{1}{\sqrt{L C}} = \frac{I_{0}}{Q_{0}}, \to T = 2 π \frac{Q_{0}}{I_{0}}, f = \frac{I_{0}}{2 π Q_{0}}$

- Bài toán ghép tụ điện nối tiếp và song song

Mạch gồm L và C1 có tần số f1 - Mạch gồm L và C2 có tần số f2

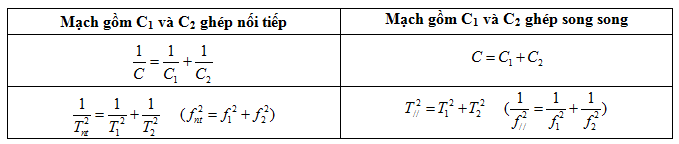
Giải Vật Lí 12 Bài 20: Mạch dao động (ảnh 1)

- Bài toán ghép cuộn cảm nối tiếp và song song

Mạch gồm L1 và C có tần số f1 - Mạch gồm L2 và C có tần số f2

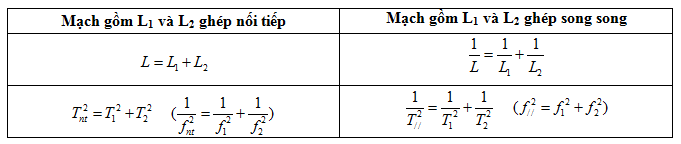
Giải Vật Lí 12 Bài 20: Mạch dao động (ảnh 2)

Ví dụ: Một mạch dao động gồm cuộn dây L và tụ điện C. Nếu dùng tụ

C_{1}

thì tần số dao động riêng của mạch là 60kHz, nếu dùng tụ

C_{2}

thì tần số dao động riêng là 80kHz. Hỏi tần số dao động riêng của mạch là bao nhiêu nếu:

a) Hai tụ $C_{1}$ và $C_{2}$ mắc song song

b) Hai tụ $C_{1}$ và $C_{2}$ mắc nối tiếp

Hướng dẫn giải

a) $C_{1} / / C_{2}$

=> $\frac{1}{f^{2}} = \frac{1}{f_{1}^{2}} + \frac{1}{f_{2}^{2}} = \frac{1}{60^{2}} + \frac{1}{80^{2}} \Rightarrow f = 48 k H z$

b) $C_{1} n t C_{2}$

=> $f^{2} = f_{1}^{2} + f_{2}^{2} = 60^{2} + 80^{2} \Rightarrow f = 100 k H z$

2. Dạng 2: Xác định I0, Q0, U0, u, i

- Từ phương trình dao động: $q = Q_{0} c o s (ω t + φ), i = q^{'} = - ω Q_{0} s i n (ω t + φ) = I_{0} c o s (ω t + φ + \frac{π}{2})$

$u = \frac{q}{C} = \frac{Q_{0}}{C} c o s (ω t + φ) = U_{0} c o s (ω t + φ)$

=> Mối liên hệ giữa các đại lượng:

$I_{0} = ω Q_{0} = \frac{Q_{0}}{\sqrt{L C}}$ , $U_{0} = \frac{Q_{0}}{C} = \frac{I_{0}}{ω C} = ω L I_{0} = I_{0} \sqrt{\frac{L}{C}}$

- Điện áp tức thời:

Cách 1: Thay vào phương trình: $u = \frac{q}{C} = \frac{Q_{0}}{C} c o s (ω t + φ) = U_{0} c o s (ω t + φ)$
Cách 2: $u^{2} = U_{0}^{2} - \frac{L}{C} i^{2} = \frac{L}{C} (I_{0}^{2} - i^{2})$

- Dòng điện tức thời:

Cách 1: Thay vào phương trình: $i = q = - ω Q_{0} s i n (ω t + φ) = I_{0} c o s (ω t + φ + \frac{π}{2})$
Cách 2: $i^{2} = I_{0}^{2} - \frac{C}{L} u^{2} = \frac{C}{L} (U_{0}^{2} - u^{2})$

- Điện tích tức thời:

Cách 1: Thay vào phương trình: $q = Q_{0} c o s (ω t + φ)$
Cách 2: $q^{2} = (C u)^{2} = Q_{0}^{2} - \frac{i^{2}}{ω^{2}} = \frac{1}{ω^{2}} (I_{0}^{2} - i^{2})$

*Chú ý:

Điện áp và cường độ dòng điện hiệu dụng: $U = \frac{U_{0}}{\sqrt{2}}; I = \frac{I_{0}}{\sqrt{2}}$

3. Dạng 3. Năng lượng của mạch dao động LC

a. Phương pháp

- Năng lượng điện trường tập trung ở trong tụ điện: $W_{d} = \frac{1}{2} C u^{2} = \frac{1}{2} q u = \frac{q^{2}}{2 C} = \frac{Q_{0}^{2}}{2 C} c o s^{2} (ω t + φ)$

- Năng lượng từ trường tập trung trong cuộn cảm: $W_{t} = \frac{1}{2} L i^{2} = \frac{Q_{0}^{2}}{2 C} \sin^{2} (ω t + φ)$

- Trong quá trình dao động của mạch, năng lượng từ và năng lượng điện trường luôn chuyển hóa cho nhau, nhưng tổng năng lượng điện từ là không đổi.

- Năng lượng điện từ: $W = W_{d} + W_{t} = \frac{1}{2} C u^{2} + \frac{1}{2} L i^{2} = \frac{1}{2} C U_{0}^{2} = \frac{Q_{0}^{2}}{2 C} = \frac{1}{2} L I_{0}^{2}$

- Vị trí năng lượng điện trường gấp $n$ lần năng từ điện trường:

${\begin{cases} W_{d} = n W_{t} \\ W = W_{t} + W_{d} \end{cases} \to {\begin{cases} W_{t} = \frac{1}{n + 1} W \\ W_{d} = \frac{n}{n + 1} W \end{cases} \to {\begin{cases} i = \pm \frac{I_{0}}{\sqrt{n + 1}} \\ u = \pm U_{0} \sqrt{\frac{n}{n + 1}} \\ q = \pm Q_{0} \sqrt{\frac{n}{n + 1}} \end{cases}$

- Mạch có cuộn dây không thuần cảm (r≠0):

Công suất tỏa nhiệt trên r hay công suất cần phải cung câp thêm cho mạch để duy trì dao động:

$P = I^{2} r = \frac{I_{0}^{2}}{2} r$

*Chú ý:

Mạch dao động có tần số góc ω, tần số f và chu kì T thì Wđ và Wt biến thiên với tần số góc 2ω, tần số 2f và chu kì T/2.
Khi tụ phóng điện thì q và u giảm và ngược lại khi tụ tích điện thì q và u tăng.

b. Ví dụ

Ví dụ 1: Một mạch dao động điều hòa, biết phương trình hiệu điện thế giữa hai bản của tụ điện là $u = 60 c o s (10^{4} π t) (V),$ điện dung của tụ điện $C = 1 μ F$ . Tính năng lượng điện từ trong khung dao động?

Hướng dẫn:

Sử dụng công thức tính năng lượng của mạch dao động: $W = \frac{1}{2} C U_{0}^{2}$

Thay U0=60 V, C=1μF vào, ta được: $W = \frac{1}{2} C U_{0}^{2} = \frac{1}{2} 10^{- 6} 60^{2} = 1, {8.10}^{- 3} (J)$

Ví dụ 2: Mạch dao động LC, với cuộn dây có

L = 5 μ F

. Cường độ dòng điện cực đại trong mạch là 2A. Khi cường độ dòng điện tức thời trong mạch là 1A thì năng lượng điện trường trong mạch là?

Hướng dẫn:

Sử dụng công thức tính năng lượng của mạch dao động: $W = W_{d} + W_{t}$

Ta có: $W = W_{d} + W_{t} = \frac{1}{2} L I_{0}^{2} \to W_{d} = W - W_{t} = \frac{1}{2} L I_{0}^{2} - \frac{1}{2} L i^{2} = \frac{L}{2} (I_{0}^{2} - i^{2}) = \frac{{5.10}^{- 6}}{2} (2^{2} - 1^{2}) = 7, {5.10}^{- 6} (J)$

4. Dạng 4. Viết phương trình dao động

Ta có:

- Phương trình điện tích trên hai bản tụ điện: $q = Q_{0} c o s (ω t + φ_{q})$

- Phương trình điện áp giữa hai bản tụ điện: $u = \frac{Q_{0}}{C} c o s (ω t + φ_{u}) = U_{0} c o s (ω t + φ_{u})$

- Phương trình điện áp dòng điện chạy trong mạch: $i = q^{'} = - Q_{0} ω s i n φ_{q} = I_{0} c o s (ω t + φ_{i})$

Trong đó:

Dòng điện, điện áp và điện tích luôn dao động cùng tần số với nhau
Điện áp và điện tích luôn dao động cùng pha: $φ_{q} = φ_{u}$
Dòng điện trong mạch dao động nhanh pha $\frac{π}{2}$ so với điện tích (điện áp) trong mạch: $φ_{i} = φ_{q} + \frac{π}{2} = φ_{u} + \frac{π}{2}$

Các bước viết phương trình dao động:

Bước 1: Xác định biên Q0, U0, I0 (tùy yêu cầu của đề bài)
Bước 2: Xác định tần số góc: $ω = \frac{1}{\sqrt{L C}} = \frac{2 π}{T} = 2 π f = \frac{I_{0}}{Q_{0}}$
Bước 3: Xác định pha ban đầu φ tại t = 0: ${\begin{cases} q = Q_{0} c o s φ \\ i = - I_{0} ω s i n φ \\ u = U_{0} c o s φ \end{cases} \to φ$

(Ta chỉ cần 2 dữ kiện q và i hoặc i và u để xác định φ)

Bước 4: Viết phương trình dao động

Lưu ý: Các bước có thể đổi vị trí cho nhau

Ví dụ:

Ví dụ 1: Trong một mạch dao động, điện tích trên tụ biến thiên theo quy luật $q = 2, 5 c o s (2 .1 0^{3} π t + \frac{π}{3}) μ C$ . Biểu thức cường độ dòng điện qua cuộn dây là:

Hướng dẫn:

Cường độ dòng điện cực đại: $I_{0} = Q_{0} ω = 2, {5.10}^{- 6} .2 {.10}^{3} π = {5.10}^{- 3} π A = 5 π m A$

$φ_{i} = φ_{q} + \frac{π}{2} = \frac{π}{3} + \frac{π}{2} = \frac{5 π}{6}$

$\to i = 5 π c o s (2 .1 0^{3} π t + \frac{5 π}{6}) m A$

Ví dụ 2: Một mạch dao động LC có tụ điện với điện dung

C = 25 p F

và cuộn cảm có độ tự cảm

L = {4.10}^{- 4} H

. Lúc t=0, dòng điện trong mạch có giá trị cực đại và bằng

20 m A

. Biểu thức của điện tích trên bản cực của tụ điện là:

Tần số góc của mạch dao động: $ω = \frac{1}{\sqrt{L C}} = \frac{1}{\sqrt{{4.10}^{- 4} {.5 .10}^{- 12}}} = 10^{7} r a d / s$ Hướng dẫn:

Điện tích cực đại giữa hai bản tụ điện: $Q_{0} = \frac{I_{0}}{ω} = \frac{{20.10}^{- 3}}{10^{7}} = {2.10}^{- 9} C = 2 n C$

Tại $t = 0, i = I_{0} c o s φ_{i} = I_{0} => φ_{i} = 0$

=> $φ_{u} = φ_{i} - \frac{π}{2} = - \frac{π}{2}$

$\to q = 2 c o s (1 0^{7} t - \frac{π}{2}) n C$

5. Dạng 5. Thời điểm điện tích trện tụ biến thiên từ q1 đến q2

(Tương tự bài toán xác định thời gian vật chuyển động từ vị trí có li độ x1 đến vị trí có li độ x2 trong dao động điều hòa)

Phương pháp: Sử dụng vòng tròn lượng giác và công thức $Δ t = \frac{Δ φ}{ω}$

Bước 1: Xác định vị trí q1 và q2 trên vòng tròn lượng giác
Bước 2: Xác định vị trí góc quay khi điện tích biến thiên từ giá trị q1 đến giá trị q2
Bước 3: Áp dụng công thức: $Δ t = \frac{Δ φ}{ω} = \frac{T Δ φ}{2 π}$

Lý thuyết Bài 20: Mạch dao động

A - TRỌNG TÂM KIẾN THỨC

1. Mạch dao động gồm một tụ điện có điện dung $C$ mắc với một cuộn cảm có độ tự cảm $L$ thành mạch kín (H20.1)

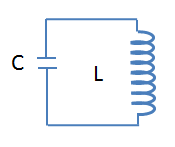
Giải Vật Lí 12 Bài 20: Mạch dao động (ảnh 3)

Nếu điện trở của mạch rất nhỏ (r=0) thì mạch là mạch dao động lí tưởng.

2. Sự biến thiên điện tích và cường độ dòng điện trong mạch dao động lí tưởng

Điện tích $q$ của một bản tụ điện và cường độ dòng điện $i$ trong mạch dao động biến thiên điều hòa theo thời gian, $i$ sớm pha $\frac{π}{2}$ so với $q$

+ $q = q_{0} c o s (ω t + φ)$

+ $i = I_{0} c o s (ω t + φ + \frac{π}{2})$

Trong đó: $I_{0} = ω q_{0}$ , $ω = \frac{1}{\sqrt{L C}}$

3. Dao động điện từ tự do

Sự biến thiên điều hòa theo thời gian của điện tích q của một bản tụ điện và cường độ dòng điện I (hoặc cường độ điện trường $\vec{E}$ và cảm ứng từ $\vec{B}$ ) trong mạch dao động được gọi là dao động điện từ tự do.

4. Chu kì và tần số dao động riêng của mạch dao động:

$T = 2 π \sqrt{L C}$ ; $f = \frac{1}{T}$ = $\frac{1}{2 π \sqrt{L C}}$

5. Năng lượng điện từ

- Năng lượng điện trường tập trung ở tụ điện:

$W_{C} = \frac{1}{2} C u^{2} = \frac{1}{2} \frac{q^{2}}{C} = \frac{1}{2 C} q_{0}^{2} \cos^{2} (ω t + φ)$

- Năng lượng từ trường tập trung ở cuộn cảm:

$W_{L} = \frac{1}{2} L i^{2} = \frac{1}{2 C} q_{0}^{2} \sin^{2} (ω t + φ)$

Tổng năng lượng điện trường trong tụ điện và năng lượng từ trường trong cuộn cảm của mạch gọi là năng lượng điện từ.

$W = W_{C} + W_{L} = \frac{1}{2} C u^{2} + \frac{1}{2} L i^{2}$

Nếu không có sự tiêu hao năng lượng thì năng lượng điện từ trong mạch sẽ được bảo toàn.

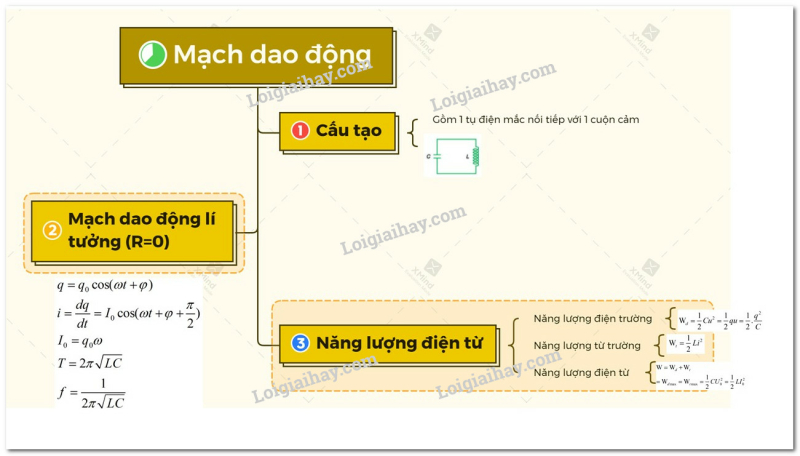
B. Sơ đồ tư duy về mạch dao động

Giải Vật Lí 12 Bài 20: Mạch dao động (ảnh 4)

Xem thêm các chương trình khác:

Bài trước

Bài sau

Giải SGK, SBT, Chuyên đề Vật Lý Lớp 12