Giải Vật Lí 12 Bài 5: Tổng hợp hai dao động điều hòa cùng phương, cùng tần số. Phương pháp giản đồ Fre-nen

79 lượt xem

Bài trước

Bài sau

Chúng tôi giới thiệu Giải bài tập Vật Lí lớp 12 Bài 5: Tổng hợp hai dao động điều hòa cùng phương, cùng tần số. Phương pháp giản đồ Fre-nen chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Tổng hợp hai dao động điều hòa cùng phương, cùng tần số. Phương pháp giản đồ Fre-nen lớp 12.

Bài giảng Vật Lí 12 Bài 5: Tổng hợp hai dao động điều hòa cùng phương, cùng tần số. Phương pháp giản đồ Fre - nen

Giải bài tập Vật Lí Lớp 12 Bài 5: Tổng hợp hai dao động điều hòa cùng phương, cùng tần số. Phương pháp giản đồ Fre-nen

Trả lời câu hỏi giữa bài

Trả lời câu C1 trang 22 SGK Vật Lí 12: Hãy biểu diễn dao động điều hòa

$x = 3 \cos (5 t + \frac{π}{3}) (c m)$ bằng một vecto quay

Lời giải:

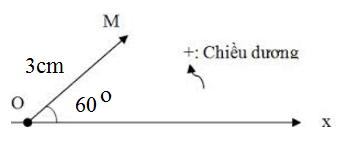
Giải Vật Lí 12 Bài 5: Tổng hợp hai dao động điều hòa cùng phương, cùng tần số. Phương pháp giản đồ Fre-nen (ảnh 1)

Biểu diễn vectơ A:

+ Có gốc tại O

+ Có độ dài là 3cm hợp với trục Ox một góc 60o

Trả lời câu C2 trang 22 SGK Vật Lí 12: Hãy tìm lại hai công thức (5.1 SGK) và (5.2 SGK).

Lời giải:

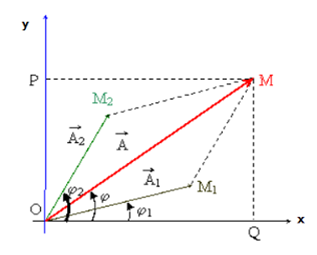
Giải Vật Lí 12 Bài 5: Tổng hợp hai dao động điều hòa cùng phương, cùng tần số. Phương pháp giản đồ Fre-nen (ảnh 2)

Ta có định lý hàm cos:

$\begin{aligned} A^{2} = A_{1}^{2} + A_{2}^{2} - 2 A_{1} A_{2} \cos [π - (φ_{2} - φ_{1})] \\ A^{2} = A_{1}^{2} + A_{2}^{2} + 2 A_{1} A_{2} \cos (φ_{2} - φ_{1}) \end{aligned}$

Theo hình vẽ: $\vec{A} = \vec{A_{1}} + \vec{A_{2}} (1)$

Chiếu (1) trục Ox:

$A \cos φ = A_{1} \cos φ_{1} + A_{2} \cos φ_{2} (2)$

Chiếu (1) trục Oy:

$A \sin φ = A_{1} \sin φ_{1} + A_{2} \sin φ_{2} (3)$

Lập tỉ số:

$\frac{(3)}{(2)} \Rightarrow \tan φ = \frac{A_{1} \sin φ_{1} + A_{2} \sin φ_{2}}{A_{1} \cos φ_{1} + A_{2} \cos φ_{2}}$

Câu hỏi và bài tập (trang 25 SGK Vật Lí 12)

Bài 1 trang 25 SGK Vật Lí 12: Nêu cách biểu diễn một dao động điều hòa bằng một vecto quay.

Lời giải:

Biểu diễn dao động điều hòa có phương trình: x = Acos(ωt + φ) (*)

Các bước:

+ Vẽ trục tọa độ Ox nằm ngang

+ Vẽ vecto OM: $\vec{O M} {\begin{matrix} (\vec{O M}, O x) = φ \\ O M = A \end{matrix}$

+ Khi t = 0 ,cho vecto OM quay đều quanh O với tốc độ góc ω.

Khi đó, vecto quay OM biểu diễn dao động điều hòa có phương trình (*)

Bài 2 trang 25 SGK Vật Lí 12: Trình bày phương pháp giản đồ Fre – nen để tìm dao động tổng hợp của hai dao động điều hòa cùng phương cùng tần số

Lời giải:

Phương pháp giản đồ Fre-nen:

+Lần lượt vẽ hai véc tơ quay biểu diễn hai phương trình dao động thành phần.

+Sau đó vẽ véc tơ tổng của hai vecto trên.

=> Vecto tổng là véc tơ quay biểu diễn phương trình của dao động tổng hợp.

Bài 3 trang 25 SGK Vật Lí 12: Nêu ảnh hưởng của độ lệch pha đến biên độ dao động của dao động tổng hợp trong các trường hợp

a) Hai dao động thành phần cùng pha

b) Hai dao động thành phần ngược pha

c) Hai dao động thành phần có pha vuông góc $φ_{2} - φ_{1} = \pm \frac{π}{2} + 2 n π$

Lời giải:

a) Hai dao động thành phần cùng pha: biên độ dao động tổng hợp là lớn nhất và bằng tổng hai biên độ: $A = A_{1} + A_{2}$

b) Hai dao động thành phần ngược pha: biên độ dao động tổng hợp là nhỏ nhất và bằng giá trị tuyệt đối của hiệu hai biên độ: $A = | A_{1} - A_{2} |$

c) Hai dao động có thành phần có pha vuông góc: $A = \sqrt{{A_{1}}^{2} + {A_{2}}^{2}}$

Bài 4 trang 25 SGK Vật Lí 12: Chọn đáp án đúng.

Hai dao động là ngược pha khi:

A. $φ_{2} - φ_{1} = 2 n π .$

B. $φ_{2} - φ_{1} = n π .$

C. $φ_{2} - φ_{1} = (n - 1) π .$

D. $φ_{2} - φ_{1} = (2 n - 1) π .$

Phương pháp giải:

Hai dao động ngược pha khi độ lệch pha của chúng bằng : φ2 - φ1 = (2n - 1)π.

Lời giải:

Hai dao động ngược pha nhau khi độ lệch pha của chúng bằng số lẻ của π

Xét các phương án:

+ Phương án A: $φ_{2} - φ_{1} = 2 n π .$ độ lệch pha của hai dao động bằng số chẵn của π => Hai dao động cùng pha

+ Phương án B: $φ_{2} - φ_{1} = n π .$ , n có thể chẵn hoặc lẻ => Hai dao động có thể cùng hoặc ngược pha nhau

+ Phương án C: n-1 cũng có thể chẵn hoặc lẻ => Hai dao động có thể cùng hoặc ngược pha nhau

+ Phương án D: 2n -1 là 1 số lẻ thỏa mãn điều kiện ngược pha của hai dao động

Đáp án: D

Bài 5 trang 25 SGK Vật Lí 12: Xét một vectơ quay

\vec{O M}

có những đặc điểm sau:

- Có độ lớn bằng hai đơn vị chiều dài.

- Quay quanh O với tốc độ góc 1 rad/s.

- Tại thời điểm t = 0, vectơ $\vec{O M}$ hợp với trục Ox một góc 300.

Hỏi vec tơ quay $\vec{O M}$ biểu diễn phương trình của dao động điều hòa nào?

A. $x = 2 c o s (t - \frac{π}{3}) .$

B. $x = 2 c o s (t + \frac{π}{6}) .$

C. $x = 2 c o s (t - 30^{\circ}) .$

D. $x = 2 c o s (t + \frac{π}{3}) .$

Phương pháp giải:

Áp dụng phương trình dao động điều hòa tổng quát x = Acos(ωt + φ).

Lời giải:

Đáp án B.

Phương trình tổng quát: x = Acos(ωt + φ).

+ Biên độ: A = 2 đơn vị chiều dài.

+ Tần số góc: ω = 1rad/s.

+ Pha ban đầu: $φ = 30^{\circ} = \frac{π}{6}$ .

Vậy vec tơ quay $\vec{O M}$ biểu diễn phương trình của dao động điều hòa $x = 2 c o s (t + \frac{π}{6}) .$

Bài 6 trang 25 SGK Vật Lí 12: Cho hai dao động điều hòa cùng phương, cùng tần số góc ω = 5π rad/s, với các biên độ:

$A_{1} = \frac{\sqrt{3}}{2} c m, A_{2} = \sqrt{3} c m$ và các pha ban đầu tương ứng $φ_{1} = \frac{π}{2}; φ_{2} = \frac{5 π}{6} .$

Tìm phương trình dao động tổng hợp của hai dao động trên.

Phương pháp giải:

Áp dụng công thức tính biên độ dao động tổng hợp : $A^{2} = A_{1}^{2} + A_{2}^{2} + 2 A_{1} A_{2} \cos (φ_{2} - φ_{1})$

Và pha ban đầu của dao động tổng hợp : $t a n φ = \frac{A_{1} \sin φ_{1} + A_{2} \sin φ_{2}}{A_{1} \cos φ_{1} + A_{2} c o s φ_{2}}$

Lời giải:

Cách 1: Phương pháp truyền thống

Áp dụng công thức tính biên độ dao động tổng hợp :

$\begin{aligned} A^{2} = A_{1}^{2} + A_{2}^{2} + 2 A_{1} A_{2} \cos (φ_{2} - φ_{1}) \\ => A^{2} = {(\frac{\sqrt{3}}{2})}^{2} + {(\sqrt{3})}^{2} \\ + 2 \frac{\sqrt{3}}{2} . \sqrt{3} . c o s (\frac{5 π}{6} - \frac{π}{2}) = \frac{21}{4} \\ => A = 2, 3 c m \end{aligned}$

Pha ban đầu của dao động tổng hợp : $t a n φ = \frac{A_{1} \sin φ_{1} + A_{2} \sin φ_{2}}{A_{1} \cos φ_{1} + A_{2} c o s φ_{2}}$

$= \frac{\frac{\sqrt{3}}{2} \sin (\frac{π}{2}) + \sqrt{3} \sin (\frac{5 π}{6})}{\frac{\sqrt{3}}{2} \cos (\frac{π}{2}) + \sqrt{3} \cos (\frac{5 π}{6})} => φ = 0, 73 π$

Phương trình dao động tổng hợp là:

$x = 2, 3 c o s (5 π t + 0, 73 π) (c m)$ .

Cách 2: Sử dụng máy tính Casio MS, fx 570 ES, fx 570 ES PLUS

Bước 1: Bấm Mode 2

Bước 2: Chuyển máy tính về chế độ rad: Shift mode 4

Bước 3: Nhập hàm $x = x_{1} + x_{2} = \frac{\sqrt{3}}{2} ∠ \frac{π}{2} + \sqrt{3} ∠ \frac{5 π}{6}$

Bước 4: Bấm shife 2 3 =

Lúc này máy tính sẽ hiện ra kết quả của x

$x = 2, 3 c o s (5 π t + 0, 73 π) (c m)$ .

Phương pháp giải bài tập tổng hợp hai dao động điều hòa cùng phương, cùng tần số

I. Nội dung lí thuyết:

Mỗi dao động điều hòa được biểu diễn bằng một véctơ quay. Véctơ này có gốc tại gốc tọa độ của trục Ox, có độ dài bằng biên độ dao động A và hợp với trục Ox một góc bằng pha ban đầu $φ$ .

- Tổng hợp hai dao động điều hòa cùng phương cùng tần số - Phương pháp giản đồ Fre-nen: Lần lượt vẽ hai véctơ quay biểu diễn hai phương trình dao động thành phần. Sau đó vẽ véctơ tổng của hai véctơ trên. Véctơ tổng la véctơ quay biểu diễn phương trình của dao động tổng hợp.

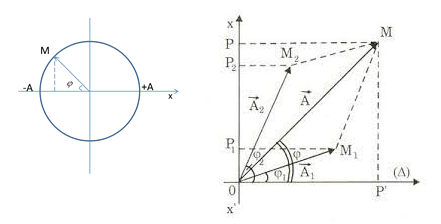
Giải Vật Lí 12 Bài 5: Tổng hợp hai dao động điều hòa cùng phương, cùng tần số. Phương pháp giản đồ Fre-nen (ảnh 1)

- Biên độ và pha ban đầu của dao động tổng hợp:

$\begin{array}{l} A^{2} = A_{1}^{2} + A_{2}^{2} + 2 A_{1} A_{2} c o s (φ_{2} - φ_{1}) \\ t a n φ = \frac{A_{1} \sin φ_{1} + A_{2} \sin φ_{2}}{A_{1} c o s φ_{1} + A_{2} c o s φ_{2}} \end{array}$

Trường hợp độ lệch pha của hai dao động đặc biệt:

$Δ φ = φ_{2} - φ_{1} = k 2 π$ : hai dao động cùng pha

$\begin{array}{l} A^{2} = A_{1}^{2} + A_{2}^{2} + 2 A_{1} A_{2} = (A_{1} + A_{2})^{2} \\ \to A = A_{1} + A_{2} \end{array}$

$Δ φ = φ_{2} - φ_{1} = (2 k + 1) π$ : hai dao động ngược pha

$\begin{array}{l} A^{2} = A_{1}^{2} + A_{2}^{2} - 2 A_{1} A_{2} = (A_{1} - A_{2})^{2} \\ \to A = | A_{1} - A_{2} | \end{array}$

$Δ φ = φ_{2} - φ_{1} = \frac{2 k + 1}{2} π$ : hai dao động vuông pha

$A^{2} = A_{1}^{2} + A_{2}^{2}$

=> Điều kiện của biên độ tổng hợp A:

$A_{min} \leq A \leq A_{max} \Leftrightarrow | A_{1} - A_{2} | \leq A \leq A_{1} + A_{2}$

II. Các dạng bài tập:

1. Dạng 1: Xác định độ lệch pha của hai dao động.

Phương pháp

$Δ φ = φ_{2} - φ_{1}$

$Δ φ = φ_{2} - φ_{1} = k 2 π$ : hai dao động cùng pha
$Δ φ = φ_{2} - φ_{1} = (2 k + 1) π$ : hai dao động ngược pha
$Δ φ = φ_{2} - φ_{1} = \frac{2 k + 1}{2} π$ : hai dao động vuông pha
$Δ φ = φ_{2} - φ_{1} = α$ : hai dao động lệch nhau một góc α

2. Dạng 2: Xác định dao động tổng hợp của hai dao động điều hòa.

Phương pháp

Cách 1: Phương pháp đại số

Bước 1: Xác định các biên độ thành phần của hai dao động và độ lệch pha giữa hai dao động.
Bước 2: Tính biên độ và pha ban đầu của dao động tổng hợp:

Bước 3: Viết ptdđ tổng hợp: $x = A c o s (ω t + φ)$

Cách 2: Sử dụng máy tính

Bấm máy tính: Chuyển máy tính về CMPLX (bấm Mode 2); Nhập số:

$A_{1} ∠ φ_{1} + A_{2} ∠ φ_{2} = s h i f t 2 3 =$ Kết quả: $A ∠ φ$

Bài tập ví dụ:

Bài 1: Một vật thực hiện đồng thời hai dao động điều hòa ${\begin{cases} x_{1} = 6 \cos 4 π t (c m) \\ x_{2} = 6 \cos (4 π t + \frac{π}{3}) (c m) \end{cases}$ . Hãy xác định dao động tổng hợp của hai dao động trên.

Hướng dẫn giải

Ta có: dao động tổng hợp có dạng: $x = A \cos (ω t + φ) (c m)$

+ Biên độ A:

$A = \sqrt{A_{1}^{2} + A_{2}^{2} + 2 A_{1} A_{2} \cos (φ_{2} - φ_{1})} = \sqrt{6^{2} + 6^{2} + 2.6.6. \cos (\frac{π}{3} - 0)} = 6 \sqrt{3} (c m)$

+ $\tan φ = \frac{A_{1} \sin φ_{1} + A_{2} \sin φ_{2}}{A_{1} \cos φ_{1} + A_{2} \cos φ_{2}} = \frac{6 \sin 0 + 6 \sin \frac{π}{3}}{6 \cos 0 + 6 \cos \frac{π}{3}} = \frac{\sqrt{3}}{3}$

$\Rightarrow φ = \frac{π}{6}$

Vậy dao động tổng hợp của hai dao động trên là:

$x = 6 \sqrt{3} \cos (4 π t + \frac{π}{6}) (c m)$

Bài 2: Một vật thực hiện đồng thời hai dao động điều hòa với biên dộ lần lượt là 3 cm và 5 cm. Trong các giá trị sau, giá trị nào không thể là biên độ của dao động tổng hợp?

A. 4 cm B. 5 cm C. 3 cm D. 10 cm

Hướng dẫn giải

Ta có: $| A_{1} - A_{2} | \leq A \leq A_{1} + A_{2}$

$\Leftrightarrow | 3 - 5 | \leq A \leq 3 + 5 \Leftrightarrow 2 \leq A \leq 8$

Vậy 10 cm không thể là biên độ của dao động tổng hợp.

Chọn D.

3. Dạng 3: Xác định dao động còn lại khi biết một dao động thành phần $x_{1} = A_{1} c o s (ω t + φ_{1})$ và dao động tổng hợp $x = A c o s (ω t + φ)$

Phương pháp

$x_{2} = A_{2} c o s (ω t + φ_{2}) .$

Trong đó:

$A_{2}^{2} = A^{2} + A_{1}^{2} - 2 A A_{1} c o s (φ - φ_{1})$
$\tan φ_{2} = \frac{A \sin φ - A_{1} \sin φ_{1}}{A c o s φ - A_{1} c o s φ_{1}}$ với $φ_{1} \leq φ \leq φ_{2}$ ( nếu $φ 1 \leq φ 2$ )

4. Dạng 4: Nếu một vật tham gia đồng thời nhiều dao động điều hoà cùng phương cùng tần số $x_{1} = A_{1} c o s (ω t + φ_{1}); x_{2} = A_{2} c o s (ω t + φ_{2})$ … thì dao động tổng hợp cũng là dao động điều hoà cùng phương cùng tần số

Phương pháp

$x = A c o s (ω t + φ) .$

Chiếu lên trục Ox và trục Oy

Ta được:

$A_{x} = A c o s φ = A_{1} c o s φ_{1} + A_{2} c o s φ_{2} + . . .$

$A_{y} = A \sin φ = A_{1} \sin φ_{1} + A_{2} \sin φ_{2} + . . .$

$\Rightarrow A = \sqrt{A_{x}^{2} + A_{y}^{2}}$ và $\tan φ = \frac{A_{y}}{A_{x}}$ với $φ \in (φ_{M i n}; φ_{M a x})$

Lý thuyết Bài 5: Tổng hợp hai dao động điều hòa cùng phương, cùng tần số - Phương pháp giản đồ FRE-NEN

I. Lý thuyết cơ bản

1. Mỗi dao động điều hòa được biểu diễn bằng một vectơ quay. Véc tơ này có:

+ gốc tại gốc tọa độ của trục Ox

+ có độ dài bằng biên độ dao động A

+ hợp với trục Ox một góc bằng pha ban đầu $φ$ (chọn chiều dương là chiều dương của vòng tròn lượng giác).

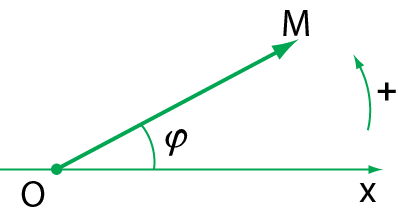
Giải Vật Lí 12 Bài 5: Tổng hợp hai dao động điều hòa cùng phương, cùng tần số. Phương pháp giản đồ Fre-nen (ảnh 2)

2. Phương pháp giản đồ Fre-nen: Lần lượt vẽ hai vec tơ quay biểu diễn hai phương trình dao động thành phần. Vectơ tổng của hai vectơ thành phàn biểu diễn phương trình của dao động tổng hợp (Hình 5.1).

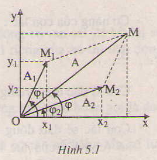
Giải Vật Lí 12 Bài 5: Tổng hợp hai dao động điều hòa cùng phương, cùng tần số. Phương pháp giản đồ Fre-nen (ảnh 3)

3. Nếu một vật tham gia đồng thời hai dao động điều hòa cùng phương, cùng tần số với các phương trình:

$x_{1} = A_{1} c o s (ω t + φ_{1}$ ) và $x_{2} = A_{2} c o s (ω t + φ_{2}$ )

Thì dao động tổng hợp sẽ là: $x = x_{1} + x_{2} = A c o s (ω t + φ$ ) với A và $φ$ được xác định bởi:

$A^{2} = A_{1}^{2} + A_{2}^{2} + 2 A_{1} A_{2} c o s (φ_{2} - φ_{1})$

$t a n φ = \frac{A_{1} s i n φ_{1} + A_{2} s i n φ_{2}}{A_{1} c o s φ_{1} + A_{2} s o s φ_{2}} .$

4. Ảnh hưởng của độ lệch pha

- Từ công thức trên ta thấy biên độ của dao động tổng hợp phụ thuộc vào các biên độ $A_{1}, A_{2}$ và độ lệch pha $(φ_{2} - φ_{1})$ của dao động thành phần.

- Nếu các dao động thành phần cùng pha, tức $Δ φ = φ_{2} - φ_{1} = 2 n π, (n = 0, \pm 1, \pm 2, . . .)$ thì biên độ dao động tổng hợp lớn nhất và bằng tổng hai biên độ: $A = A_{1} + A_{2}$

- Nếu các dao động thành phần ngược pha, tức $Δ φ = φ_{2} - φ_{1} = (2 n + 1) π, (n = 0, \pm 1, \pm 2, . . .)$ thì biên độ dao động tổng hợp nhỏ nhất nhất và bằng hiệu hai biên độ: $A = | A_{1} - A_{2} |$

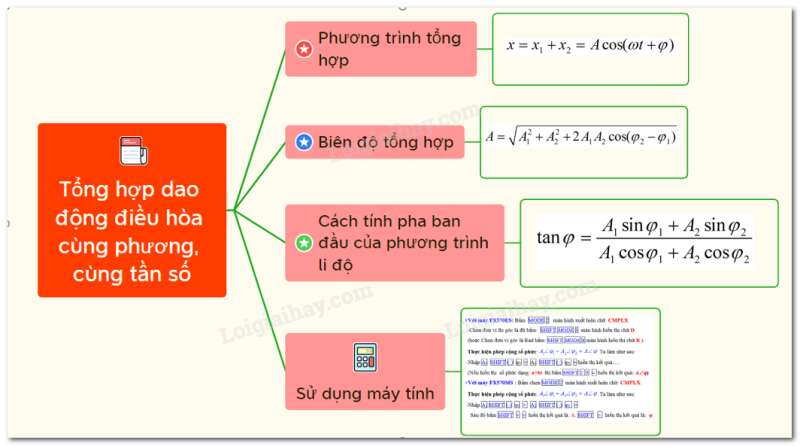
II. Sơ đồ tư duy về tổng hợp dao động điều hòa cùng phương, cùng tần số. Phương pháp giản đồ Fre-nen

Giải Vật Lí 12 Bài 5: Tổng hợp hai dao động điều hòa cùng phương, cùng tần số. Phương pháp giản đồ Fre-nen (ảnh 4)

Xem thêm các chương trình khác:

Bài trước

Bài sau

Giải SGK, SBT, Chuyên đề Vật Lý Lớp 12