Giải Vật Lí 12 Bài 3: Con lắc đơn

95 lượt xem

Bài trước

Bài sau

Chúng tôi giới thiệu Giải bài tập Vật Lí lớp 12 Bài 3: Con lắc đơn chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Con lắc đơn lớp 12.

Bài giảng Vật Lí 12 Bài 3: Con lắc đơn

Giải bài tập Vật Lí Lớp 12 Bài 3: Con lắc đơn

Trả lời câu hỏi giữa bài

Trả lời câu C1 trang 15 SGK Vật Lí 12: Chứng tỏ rằng đối với những góc lệch nhỏ hơn 20o thì độ chênh lệch giữa sinα và α (rad) không đến 1%.

Lời giải:

Ta kiểm nghiệm với các góc lệch nhỏ bằng 20o, ta có sinα ≈ α (rad)

$\begin{aligned} \sin 20^{o} = 0, 3420 \\ 20^{o} = \frac{20. π}{180} = 0, 3491 (r a d) \end{aligned}$

Do đó độ chênh lệch giữa sinα và α là:

0,3491 – 0,3420 = 0,0071 = 0,7%

Trả lời câu C2 trang 15 SGK Vật Lí 12: Có nhận xét gì về chu kì của con lắc đơn?

Lời giải:

Chu kì con lắc

$T = 2 π \sqrt{\frac{l}{g}}$

Ta thấy chu kì T phụ thuộc vào chiều dài dây l và gia tốc trọng trường g.

T tỉ lệ với căn bậc hai của chiều dài l và tỉ lệ nghịch căn bậc hai của gia tốc trọng trường g.

T tăng khi chiều dài l tăng hoặc gia tốc trọng trường giảm

T giảm khi chiều dài l giảm hoặc gia tốc trọng trường tăng.

Trả lời câu C3 trang 16 SGK Vật Lí 12: Hãy mô tả một cách định tính sự biến đổi năng lượng của con lắc, khi nó đi từ vị trí biên về vị trí cân bằng và khi nó đi từ vị trí cân bằng ra vị trí biên.

Lời giải:

Khi con lắc đi từ vị trí biên về vị trí cân bằng thì : s giảm (thế năng giảm), v tăng (động năng tăng).

- Tại vị trí cân bằng: s = 0 (thế năng bằng 0), v cực đại (động năng cực đại).

- Khi con lắc đi từ vị trí cân bằng đến vị trí biên: s tăng (thế năng tăng), v giảm (động năng giảm)

- Tại vị trí biên: s cực đại (thế năng cực đại), v = 0 (động năng bằng 0).

Vậy: Trong quá trình dao động đi từ vị trí biên đến vị trí cân bằng hay đi từ vị trí cân bằng đến vị trí biên, khi động năng tăng thì thế năng giảm và ngược lại.

Câu hỏi và bài tập (trang 17 SGK Vật Lí 12)

Bài 1 trang 17 SGK Vật Lí 12: Thế nào là con lắc đơn khảo con lắc đơn về mặt động lực học. Chứng minh rằng khi dao động nhỏ ( $\sin α \approx α (r a d)$ ), dao động của con lắc đơn là dao động điều hòa.

Lời giải:

- Con lắc đơn gồm một vật nhỏ , khối lượng m, treo ở đầu một sợi dây không dãn, không đáng kể, dài l.

- Vị trí cân bằng của con lắc là vị trí mà dây treo có phương thằng đứng. Con lắc sẽ đứng yên mãi ở vị trí này nếu lúc đầu nó đứng yên. Kéo nhẹ quả cầu cho dây treo lệch khỏi vị trí cân bằng một góc rồi thả ra, ta thấy con lắc dao động quanh vị trí cân bằng trong mặt phẳng đứng đi qua điểm treo và vị trí ban đầu của vật.

- Khi con lắc dao động nhỏ (sinα ≈ α) (rad), dao động của con lắc đơn là dao động điều hòa.

Bài 2 trang 17 SGK Vật Lí 12: Viết công thức tính chu kì của con lắc đơn khi dao động nhỏ.

Lời giải:

Khi dao động nhỏ (sinα ≈ α (rad)), con lắc đơn dao động điều hòa với chu kì: $T = 2 π \sqrt{\frac{l}{g}}$

Bài 3 trang 17 SGK Vật Lí 12: Viết biểu thức của động năng, thế năng, cơ năng của con lắc đơn ở vị trí có góc lệch α bất kỳ. Khi con lắc dao động thì động năng và thế năng của con lắc biến thiên như thế nào?

Lời giải:

Động năng của con lắc đơn: $W_{đ} = \frac{1}{2} m v^{2}$

Thế năng của con lắc đơn ở li độ góc α :

$W_{t} = m g l (1 - c o s α)$ (mốc thế năng ở vị trí cân bằng)

Cơ năng của con lắc đơn được bảo toàn nếu bỏ qua mọi ma sát:

$W = \frac{1}{2} m v^{2} + m g l (1 - c o s α)$ = hằng số

Vì cơ năng của con lắc đơn được bảo toàn nếu bỏ qua mọi ma sát, nên khi con lắc dao động, thì : khi động năng tăng một lượng bao nhiêu thì thế năng giảm một lượng bấy nhiêu và ngược lại.

Bài 4 trang 17 SGK Vật Lí 12: Hãy chọn đáp án đúng.

Chu kì của con lắc đơn dao động nhỏ (sinα ≈ α (rad)) là:

A. $T = \frac{1}{2 π} \sqrt{\frac{l}{g}}$ .

B. $T = \frac{1}{2 π} \sqrt{\frac{g}{l}}$

C. $T = \sqrt{2 π \frac{l}{g}}$

D. $T = 2 π \sqrt{\frac{l}{g}}$

Phương pháp giải:

Sử dụng công thức tính chu kỳ của con lắc đơn

T = 2 π \sqrt{\frac{l}{g}}

Lời giải:

Chu kì của con lắc đơn dao động nhỏ (sinα ≈ α (rad)) là: $T = 2 π \sqrt{\frac{l}{g}}$

Đáp án: D

Bài 5 trang 17 SGK Vật Lí 12: Hãy chọn câu đúng.

Một con lắc đơn dao động với biên độ góc nhỏ. Chu kì của con lắc không thay đổi khi:

A. Thay đổi chiều dài của con lắc.

B. Thay đổi gia tốc trọng trường.

C. Tăng biên độ góc đến 300.

D. Thay đổi khối lượng của con lắc.

Phương pháp giải:

Sử dụng công thức tính chu kỳ của con lắc đơn

T = 2 π \sqrt{\frac{l}{g}}

Lời giải:

Đáp án: D.

Sử dụng công thức tính chu kỳ của con lắc đơn $T = 2 π \sqrt{\frac{l}{g}}$ ta thấy chu kỳ của con lắc đơn chỉ phụ thuộc vào g và l mà không phụ thuộc vào khối lượng vật nặng m. Vậy khi thay đổi khối lượng của con lắc thì chu kỳ của con lắc đơn không thay đổi

Bài 6 trang 17 SGK Vật Lí 12: Một con lắc đơn khi được thả không vận tốc đầu từ li độ góc α0. Khi con lắc đi qua vị trí cân bằng thì tốc độ của quả cầu con lắc là bao nhiêu?

A. $\sqrt{g l (1 - c o s α_{0})}$

B. $\sqrt{2 g l c o s α_{0}}$

C. $\sqrt{2 g l (1 - c o s α_{0})}$

D. $\sqrt{g l c o s α_{0}}$

Phương pháp giải:

Áp dụng định luật bảo toàn cơ năng

\frac{1}{2} m v_{m a x}^{2} = m g l (1 - c o s α_{0})

Lời giải:

Khi con lắc qua vị trí cân bằng thì thế năng bằng 0, động năng cựa đại (bằng cơ năng):

$\begin{array}{l} \frac{1}{2} m v_{m a x}^{2} = m g l (1 - c o s α_{0}) \\ \Rightarrow v_{m a x} = \pm \sqrt{2 g l (1 - c o s α_{0})} \end{array}$

Đáp án C.

Bài 7 trang 17 SGK Vật Lí 12: Một con lắc đơn dài l = 2,00 m, dao động điều hòa tại một nơi có gia tốc rơi tự do g = 9,80 m/s2. Hỏi con lắc thực hiện được bao nhiêu dao động toàn phần trong 5,00 phút?

Phương pháp giải:

Áp dụng công thức tính chu kỳ của con lắc đơn

T = 2 π \sqrt{\frac{l}{g}}

Lời giải:

Tần số của con lắc đơn $f = \frac{1}{T} = \frac{1}{2 π} \sqrt{\frac{g}{l}} = \frac{1}{2 π} \sqrt{\frac{9, 8}{2}} \approx 0, 3523$

Ta có tần số là số dao động vật thực hiện được trong $1 s$

=> Số dao động toàn phần mà con lắc thực hiện được trong thời gian $t = 5$ phút $= 5.60 = 300 s$ là:

$N = f . t = 0, 3523.300 = 105, 69 \approx 106$ dao động

Phương pháp giải một số dạng bài tập về con lắc đơn

Tổng hợp cách giải một số dạng bài tập về con lắc đơn thường gặp

Dạng 1: Chu kì con lắc đơn thay đổi theo chiều dài

Chu kì con lắc đơn ban đầu khi chưa có sự thay đổi là:

$T_{1} = \frac{1}{f} = 2 π \sqrt{\frac{l_{1}}{g}} = \frac{Δ t}{N_{1}}$

Chu kì của con lắc đơn sau khi có sự thay đổi là:

$T_{2} = \frac{1}{f} = 2 π \sqrt{\frac{l_{2}}{g}} = \frac{Δ t}{N_{2}}$

=> $\frac{T_{1}}{T_{2}} = \sqrt{\frac{l_{1}}{l_{2}}} = \frac{N_{2}}{N_{1}}$

Trong đó N là số dao động toàn phần vật thực hiện được trong thời gian $Δ t$

*Bài toán con lắc vướng đinh:

+ Chu kì con lắc trước khi vướng đinh là: $T_{1} = 2 π \sqrt{\frac{l_{1}}{g}}$

+ Chu kì của con lắc sau khi vướng đinh là: $T_{2} = 2 π \sqrt{\frac{l_{2}}{g}}$

=> Chu kì của con lắc là: $T = \frac{1}{2} (T_{1} + T_{2})$

Bài tập ví dụ:

Một con lắc đơn có chiều dài l. Trong khoảng thời gian $Δ t$ nó thực hiện 12 dao động. Khi giảm độ dài của nó bớt 16 cm, trong cùng khoảng thời gian $Δ t$ như trên, con lắc thực hiện 20 dao động. Tính độ dài ban đầu của con lắc.

Hướng dẫn giải

Ta có: $\frac{T_{1}}{T_{2}} = \sqrt{\frac{l_{1}}{l_{2}}} = \frac{N_{2}}{N_{1}} \Leftrightarrow \sqrt{\frac{l}{l - 0, 16}} = \frac{20}{12} \Leftrightarrow l = 0, 25 m$

Dạng 2: Xác định các đại lượng cơ bản trong dao động điều hòa của con lắc đơn

- Tìm $ω, T, f$ : Đề cho l, g:

$ω = \sqrt{\frac{g}{l}}, T = \frac{2 π}{ω} = 2 π \sqrt{\frac{l}{g}}, f = \frac{ω}{2 π} = \frac{1}{2 π} \sqrt{\frac{g}{l}}$

- Tìm gia tốc rơi tự do:

$T = \frac{2 π}{ω} = 2 π \sqrt{\frac{l}{g}} \to g = \frac{4 π^{2} l}{T^{2}}$

Dạng 3: Tìm $ω, T, f$ : thay đổi chiều dài dây treo l

Trong cùng khoảng thời gian t, hai con lắc thực hiện N1 và N2 dao động:
$f = \frac{N}{t} \to \frac{g}{l} = ω^{2} = (2 π f)^{2} = (\frac{2 π N}{t})^{2} \to \frac{l_{2}}{l_{1}} = (\frac{N_{1}}{N_{2}})^{2}$
Thay đổi chiều dài con lắc:
Ta có: $T^{2} \sim l, f^{2} \sim \frac{1}{l}, ω^{2} \sim \frac{1}{l}$

Ta suy ra:

$(\frac{ω_{1}}{ω_{2}})^{2} = (\frac{f_{1}}{f_{2}})^{2} = \frac{l_{2}}{l_{1}} = \frac{l_{1} \pm Δ l}{l_{1}}$

Ta có: $T_{1} = 2 π \sqrt{\frac{ℓ_{1}}{g}} \Rightarrow T_{1}^{2} = 4 π^{2} . \frac{ℓ_{1}}{g}; T_{2} = 2 π \sqrt{\frac{ℓ_{2}}{g}} \Rightarrow T_{2}^{2} = 4 π^{2} . \frac{ℓ_{2}}{g}$

Chu kỳ của con lắc có chiều dài $ℓ_{3} = ℓ_{1} \pm ℓ_{2}$ là: $T_{3} = 2 π \sqrt{\frac{ℓ_{1} + ℓ_{2}}{g}} \Rightarrow T_{3}^{2} = 4 π^{2} . (\frac{ℓ_{1} \pm ℓ_{2}}{g}) = T_{1}^{2} \pm T_{2}^{2}$

Dạng 4: Viết phương trình dao động điều hòa của con lắc đơn

Bước 1: Xác định biên độ góc: $S_{0}, α_{0} .$

Sử dụng các dữ kiện đầu bài cho và hệ thức độc lập với thời gian: $s_{0}^{2} = s^{2} + \frac{v^{2}}{ω^{2}}$ hay $α_{0}^{2} = α^{2} + \frac{v^{2}}{l^{2} ω^{2}}$ hoặc $α_{0}^{2} = α^{2} + \frac{v^{2}}{l g}$

Bước 2: Xác định tần số góc ω: $ω = \sqrt{\frac{g}{l}} = \frac{2 π}{T} = 2 π f$
Bước 3: Xác định pha ban đầu: $φ$

Tại $t = 0 : {\begin{cases} s = s_{0} c o s φ \\ v = - ω s_{0} \sin φ \end{cases}$

Bước 4: Viết PTDĐ: $s = s_{0} c o s (ω t + φ) h a y α = α_{0} c o s (ω t + φ)$

Với $s_{0} = l α_{0}$

Bài tập ví dụ: Một con lắc đơn có chiều dài l = 16 cm. Kéo con lắc lệch khỏi vị trí cân bằng một góc 90 rồi thả nhẹ. Bỏ qua mọi ma sát, lấy g = 10 m/s2. Chọn gốc thời gian là lúc thả vật, chiều dương cùng chiều với chiều chuyển động ban đầu của vật. Viết phương trình dao động theo li độ góc tính ra rad.

Hướng dẫn giải

Ta có: phương trình dao động theo li độ góc của con lắc đơn có dạng:

$α = α_{0} \cos (ω t + φ)$

Kéo con lắc lệch khỏi VTCB một góc 90 rồi thả nhẹ => $α_{0} = 9^{0} = \frac{π}{20} = 0, 157 r a d$

$ω = \sqrt{\frac{g}{l}} = 2, 5 π r a d / s$

Tại thời điểm t = 0 ta có:

$α = α_{0} \cos φ \Rightarrow \cos φ = \frac{α}{α_{0}} = \frac{- α_{0}}{α_{0}} = - 1 \Rightarrow φ = π$

Vậy $α = 0, 157 \cos (2, 5 π + π) (r a d)$

Dạng 5: Tính vận tốc vật ở li góc $α$ bất kì

Phương pháp

$v_{α} = \pm \sqrt{2 g l (c o s α - c o s α_{0})}$

Đặc biệt:

Nếu $α_{0} \leq 10^{0}$ thì có thể tính gần đúng: $v_{α} = \pm \sqrt{g l ({α_{0}}^{2} - α^{2})}$
Khi vật qua vị trí cân bằng: $v_{V T C B} = v_{m a x} = \sqrt{2 g l (1 - c o s α_{0})}$

Khi $α_{0} \leq 10^{0}$ thì $v_{m a x} = α_{0} \sqrt{g l} = ω S_{0}$

Dạng 6: Tính lực căng dây ở li độ góc $α$ bất kì

Phương pháp

$T = m g (3 c o s α - 2 c o s α_{0})$

Vị trí đặc biệt:
Khi qua vị trí cân bằng: $α = 0 \to c o s α = 1 \to T_{m a x} = m g (3 - 2 c o s α_{0})$
Khi đến vị trí biên: $α = \pm α_{0} \to c o s α = c o s α_{0} \to T_{m i n} = m g (c o s α_{0})$
Khi $α_{0} \leq 10^{0}$ : ta có thể viết:

$\begin{array}{l} T = m g (1 - 1, 5 α^{2} + {α_{0}}^{2}) \\ \to T_{m a x} = m g (1 + {α_{0}}^{2}), T_{m i n} = m g (1 - 0, 5 {α_{0}}^{2}) \end{array}$

Dạng 7: Năng lượng dao động, vận tốc, lực căng dây của con lắc đơn

- Thế năng: $W_{t} = m g h = m g l (1 - \cos α)$

- Động năng: $W_{d} = \frac{1}{2} m v^{2} = m g l (\cos α - \cos α_{0})$

- Cơ năng: $W = W_{t} + W_{d} = m g l (1 - \cos α_{0})$

- Vận tốc: ${\begin{cases} v = \sqrt{2 g l . (\cos α - \cos α_{0})} \\ v_{max} = \sqrt{2 g l . (1 - \cos α_{0})} \end{cases}$

- Lực căng dây: $T = m g (3 \cos α - 2 \cos α_{0})$

+ $T_{max} = m g (3 - 2 \cos α_{0})$ (khi vật qua vị tri cân bằng)

+ $T_{min} = m g . \cos α_{0}$ (khi vật ở vị trí biên)

*Lưu ý:

Nếu $α_{0} \leq 10^{0}$ thì ${\begin{cases} W_{t} = \frac{1}{2} m g l α^{2} \\ W_{d} = \frac{1}{2} m g l (α_{0}^{2} - α^{2}) \end{cases} \Rightarrow W = \frac{1}{2} m g l α_{0}^{2}$

(Với $α, α_{0}$ tính ra rad).

Dạng 8: Sự thay đổi chu kì của con lắc đơn khi chịu thêm tác dụng của lực lạ

1. Các lực lạ thường gặp

- Lực quán tính: $\vec{F} = - m \vec{a}$ , độ lớn F = ma ( $\vec{F} ↑↓ \vec{a}$ )

*Chú ý

+ Chuyển động nhanh dần đều $\vec{a} ↑↑ \vec{v}$ ( $\vec{v}$ có hướng chuyển động)

+ Chuyển động chậm dần đều $\vec{a} ↑↓ \vec{v}$

- Lực điện trường: $\vec{F} = q \vec{E}$ , độ lớn F = |q|E (Nếu q > 0 Þ $\vec{F} ↑↑ \vec{E}$ ; còn nếu q < 0 Þ $\vec{F} ↑↓ \vec{E}$ )

- Lực đẩy Ácsimét: $F = D g V$ ( $\vec{F}$ luông thẳng đứng hướng lên)

Trong đó:

D là khối lượng riêng của chất lỏng hay chất khí.
g là gia tốc rơi tự do.
V là thể tích của phần vật chìm trong chất lỏng hay chất khí đó.

2. Công thức áp dụng làm bài tập

- $\vec{F}$ có phương ngang: $\vec{F} ⊥ \vec{P}$

Tại VTCB dây treo lệch với phương thẳng đứng một góc có: $\tan α = \frac{F}{P}$

Thì $g^{'} = \sqrt{g^{2} + {(\frac{F}{m})}^{2}}$

Ví dụ:

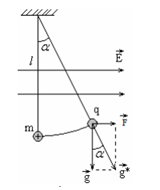
Giải Vật Lí 12 Bài 3: Con lắc đơn (ảnh 1)

- $\vec{F}$ có phương thẳng đứng thì $g^{'} = g \pm \frac{F}{m}$

Nếu $\vec{F}$ hướng xuống thì $g^{'} = g + \frac{F}{m}$
Nếu $\vec{F}$ hướng lên thì $g^{'} = g - \frac{F}{m}$

- $\vec{F}$ có hướng xiên:

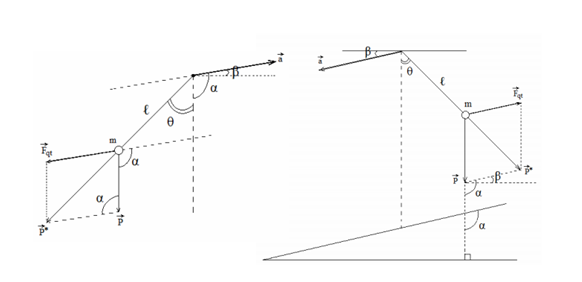
Giải Vật Lí 12 Bài 3: Con lắc đơn (ảnh 2)

Xiên xuống:

$\begin{array}{l} P^{'} = \sqrt{P^{2} + F_{q t}^{2} - 2 P . F_{q t} c o s (90^{0} + β)} \\ \to g^{'} = \sqrt{g^{2} + a^{2} - 2 g . a c o s (9 0^{0} + β)} \end{array}$

Góc θ: $\frac{a}{\sin θ} = \frac{g^{'}}{\sin (90^{0} + β)}$

Xiên lên:

$\begin{array}{l} P^{'} = \sqrt{P^{2} + F_{q t}^{2} - 2 P . F_{q t} c o s (90^{0} - β)} \\ \to g^{'} = \sqrt{g^{2} + a^{2} - 2 g . a c o s (9 0^{0} - β)} \end{array}$

Vì $c o s (π - a) = - c o s a$

$\to P^{'} = \sqrt{P^{2} + F_{q t}^{2} + 2 P . F_{q t} c o s α}$

Góc θ: $\frac{a}{\sin θ} = \frac{g^{'}}{\sin (90^{0} - β)}$

Dạng 9: Bài tập sự nhanh chậm của đồng hồ quả lắc

1. Phương pháp chung

Gọi T1 là chu kì chạy đúng, T2 là chu kì chạy sai

Trong thời gian T1(s) đồng hồ chạy sai |T2-T1| (s)

=> 1(s) đồng hồ chạy sai $\frac{| T_{2} - T_{1} |}{T_{1}} s$

Vậy trong khoảng thời gian ∆t, đồng hồ chạy sai: $θ = Δ t \frac{| T_{2} - T_{1} |}{T_{1}} s$

Các bước giải:

- Bước 1: Thiết lập tỉ số $\frac{T_{2}}{T_{1}}$

- Bước 2: Biện luận:

Nếu: $\frac{T_{2}}{T_{1}} > 1 \to T_{2} > T_{1}$ : Chu kì tăng => Đồng hồ chạy chậm lại
Nếu $\frac{T_{2}}{T_{1}} < 1 \to T_{2} < T_{1}$ : Chu kì giảm => Đồng hồ chạy nhanh lên

- Bước 3: Xác định thời gian chạy nhau hay chậm bằng công thức: $θ = Δ t \frac{| T_{2} - T_{1} |}{T_{1}} = Δ t | \frac{T_{2}}{T_{1}} - 1 | s$

2. Các dạng bài tập

a) Xác định thời gian đồng hồ chạy sai khi thay đổi nhiệt độ.

- Khi thay đổi nhiệt độ, chiều dài của con lắc thay đổi theo biểu thức: $l = l_{0} (1 + α t)$

l0: chiều dài dây treo (kim loại) ở 00C
l: chiều dài dây treo (kim loại) ở t0C
α: hệ số nở dài của dây treo kim loại

Ở nhiệt độ t1 đồng hồ chạy đúng, nhiệt độ t2 đồng hồ chạy sai:

- Xét tỉ số: $\frac{T_{2}}{T_{1}}$

Ta có: $\frac{T_{2}}{T_{1}} = \sqrt{\frac{l_{2}}{l_{1}}} = \sqrt{\frac{l_{0} (1 + α (t_{2})}{l_{0} (1 + α t_{1})}} = \sqrt{\frac{(1 + α t_{2})}{(1 + α t_{1})}} = (1 + α t_{2})^{\frac{1}{2}} (1 + α t_{1})^{- \frac{1}{2}}$

Sử dụng công thức gần đúng: ${\begin{cases} {(1 \pm x)}^{n} \approx 1 \pm n x \\ (1 + x_{1}) (1 - x_{2}) \approx 1 + x_{1} - x_{2} \end{cases}$ với x, x1, x2 << 1

Vì αt1 và αt2<< 1 $\to (1 + α t_{2})^{\frac{1}{2}} (1 + α t_{1})^{- \frac{1}{2}} \approx (1 + \frac{1}{2} λ t_{2}) (1 - \frac{1}{2} λ t_{1}) \approx 1 + \frac{1}{2} α t_{2} - \frac{1}{2} α t_{1} \approx 1 + \frac{1}{2} α (t_{2} - t_{1})$

$\to θ = Δ t \frac{| T_{2} - T_{1} |}{T_{1}} = Δ t | \frac{T_{2}}{T_{1}} - 1 | = Δ t . \frac{1}{2} α (t_{2} - t_{1}) (s)$

*Chú ý:

Nếu t2 > t1: đồng hồ chạy chậm lại và ngược lại t2 < t1: đồng hồ chạy nhanh lên.

b) Xác định thời gian đồng hồ chạy sai ở độ cao h và độ sâu d so với mực nước biến (coi nhiệt độ không đổi)

Khi đưa con lắc lên độ cao h hay xuống độ sâu d thì gia tốc rơi tự do g thay đổi.

Ở mực nước biển đồng hồ chạy đúng, khi đưa lên độ cao h:

${\begin{cases} \frac{T_{2}}{T_{1}} = \sqrt{\frac{g}{g_{h}}} \\ g_{h} = g \frac{R^{2}}{{(R + h)}^{2}} \end{cases} \to \frac{T_{2}}{T_{1}} = \frac{(R + h)}{R} = 1 + \frac{h}{R}$

$\to θ = Δ t \frac{| T_{2} - T_{1} |}{T_{1}} = Δ t | \frac{T_{2}}{T_{1}} - 1 | = Δ t \frac{h}{R} (s)$

Ta thấy $\frac{T_{2}}{T_{1}} = 1 + \frac{h}{R} > 1 \to T_{2} > T_{1}$ => Đồng hồ chạy chậm lại

Ở mực nước biển đồng hồ chạy đúng, khi đưa đồng hồ xuống độ sâu h thì đồng hồ chạy sai.

${\begin{cases} \frac{T_{2}}{T_{1}} = \sqrt{\frac{g}{g_{d}}} \\ g_{d} = g \frac{(R - d)}{R} \end{cases} \to \frac{T_{2}}{T_{1}} = \sqrt{\frac{R}{(R - d)}} = \sqrt{\frac{1}{1 - \frac{d}{R}}} = {(1 - \frac{d}{R})}^{- \frac{1}{2}} \approx 1 + \frac{1}{2} \frac{d}{R}$

$\to θ = Δ t \frac{| T_{2} - T_{1} |}{T_{1}} = Δ t | \frac{T_{2}}{T_{1}} - 1 | = Δ t \frac{1}{2} \frac{d}{R} (s)$

*Chú ý:

Khi đưa con lắc lên cao hoặc xuống sâu, chu kì đều tăng nên suy ra đồng hồ luôn chạy chậm

c) Xác định thời gian đồng hồ chạy sai khi thay đổi vị trí trên trái đất (nhiệt độ không đổi)

Tại nơi có gia tốc trọng trường g1 đồng hồ chạy đúng với: $T_{1} = 2 π \sqrt{\frac{l}{g_{1}}}$

Tại nơi có gia tốc trọng trường g2 đồng hồ chạy sai: $T_{1} = 2 π \sqrt{\frac{l}{g_{2}}}$

$\to \frac{T_{2}}{T_{1}} \approx 1 - \frac{1}{2} \frac{Δ g}{g_{1}} \to \frac{T_{2} - T_{1}}{T_{1}} = - \frac{1}{2} \frac{Δ g}{g_{1}}$

TỔNG QUÁT: Xác định thời gian đồng hồ chạy sai khi 1 hoặc nhiều yếu tố thay đổi.

$\frac{Δ T}{T} = \frac{T_{2} - T_{1}}{T_{1}} = \frac{1}{2} α (t_{2} - t_{1}) + \frac{h}{R} + \frac{1}{2} \frac{d}{R} - \frac{1}{2} \frac{Δ g}{g_{1}}$

Dạng 10: Bài toán con lắc vướng đinh

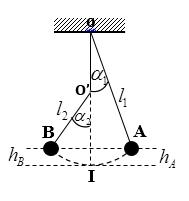
Giải Vật Lí 12 Bài 3: Con lắc đơn (ảnh 3)

Phương pháp:

Một con lắc đơn đang dao động điều hòa với chiều dài ℓ1 thì con lắc vướng đinh làm cho nó dao động với ℓ2 nên chu kì, tần số góc, biên độ góc,… cũng thay đổi theo.

Chu kì T của CLVĐ:

$T = \frac{1}{2} (T_{1} + T_{2}) \to T = \frac{π}{\sqrt{g}} (\sqrt{l_{1}} + \sqrt{l_{2}})$
Độ cao CLVĐ so với VTCB :

Vì $W_{A} = W_{B} \Rightarrow h_{A} = h_{B}$

Tỉ số biên độ dao động 2 bên VTCB

– Góc lớn (α0>100):

Vì $h_{A} = h_{B}$

→ℓ1 (1–cosα1) = ℓ2(1–cosα2)

$\to \frac{l_{1}}{l_{2}} = \frac{1 - c o s α_{2}}{1 - c o s α_{1}}$
– Góc nhỏ:

$(α_{0} \leq 10^{0}) \to c o s α \approx 1 - α^{2} / 2) :\to \frac{l_{1}}{l_{2}} = (\frac{α_{2}}{α_{1}})^{2}$

Dạng 11: Sự trùng phùng của hai con lắc

Xét 2 con lắc dao động trong 2 mặt phẳng song song, con lắc 1 có chu kì T1, con lắc hai có chu kì T2 (T1>T2). Tại thời gian t = 0 hai con lắc có cùng 1 trạng thái (VD: cùng qua VTCB theochiều + chẳng hạn), sau thời gian nào đó trạng thái của 2 con lắc lại giống như trạng thái lúc t = 0 (tức lại cùng qua VTCB theo chiều +) được gọi là sự trùng phùng.

Phương pháp:

Thời gian ∆t nhỏ nhất kể từ khi thời điểm t = 0 cho tới lúc 2 còn lắc trùng phùng lần thứ nhất gọi là chu kì trùng phùng.

Vì con lắc 2 có chu kì nhỏ hơn con lắc 1 nên sau lần dao động thứ nhất của con lắc 2 con lắc 1 cần 1 thời gian (T1-T2) để trở về vị trí xuất phát ban đầu của nó. Nói cách khác là con lắc 1 bị trễ so với con lắc 2 là (T1-T2).
Sau n lần dao động của con lắc 2 khoảng thời gian trễ này sẽ là $n . (T_{1} - T_{2})$ . Để sự trùng phùng xảy ra thì khoảng thời gian trễ trên phải đúng bằng một chu kì T2. Hay:

$\begin{array}{l} n (T_{1} - T_{2}) = T_{2} \leftrightarrow n T_{1} = (n + 1) T_{2} = Δ t \\ \to Δ τ = \frac{T_{1} T_{2}}{| T_{1} - T_{2} |} \end{array}$

hoặc $Δ t = b T_{1} = a T_{2}$ , trong đó: $\frac{T_{1}}{T_{2}} = \frac{a}{b}$ (phân số tối giản)

*Chú ý:

Thời gian trùng phùng lần đầu kể từ lúc t = 0 cũng chính là chu kì trùng phùng $Δ τ$

Bài tập ví dụ:

Hai con lắc dao động điều hòa với chu kì lần lượt là $T_{1} = 2 s; T_{2} = 1, 5 s$ . Giả sửtại thời điểm t hai con lăc cùng qua vị trí cân bằng theo cùng chiều thì sau đó bao lâu cả hai con lắc cùng qua vị trí cân bằng theo cùng chiều như trên.

Hướng dẫn giải

Gọi thời gian của hai con lắc cùng qua vị trí cân bằng theo cùng chiều là $Δ t$ (còn gọi là khoảng thời gian giữa hai lần trùng phùng liên tiếp).

Ta có: $Δ t = N_{1} T_{1} = N_{2} T_{2}$

Theo bài ra ta có: $\frac{T_{1}}{T_{2}} = \frac{N_{2}}{N_{1}} = \frac{2}{1, 5} = \frac{4}{3}$ = phân số tối giản => ${\begin{cases} N_{1} = 3 n \\ N_{2} = 4 n \end{cases} (n \in N *)$

Thời gian trùng phùng lần đầu tiên ứng với n = 1. Lúc đó con lắc 1 thực hiện được 3 dao động thì con lắc 2 thực hiện được 4 dao động nên thời gian trùng phùng là:

$Δ t = 3 T_{1} = 3.2 = 6 s$ đối với con lắc 1 hoặc có thể là $Δ t = 4 T_{2} = 4.1, 5 = 6 s$ đối với con lắc thứ hai

Lý thuyết Bài 3: Con lắc đơn

1. Với con lắc đơn, thành phần lực kéo vật về vị trí cân bằng là

$P_{1} = - m g \frac{s}{l} = m a = m s "$ hay $s "= - g \frac{s}{l} = - ω^{2} s$

Trong đó, s là li độ cong của vật đo bằng mét (m), l là chiều dài của con lắc đơn đo bằng mét (m).

Đó là phương trình động lực học của con lắc đơn.

2. Con lắc đơn dao động điều hòa với phương trình:

$s = S_{0} c o s (ω t + φ)$ hoặc $α = α_{0} c o s (ω t + φ)$ ; với $α = \frac{s}{l}$ ; $α_{0} = \frac{S_{0}}{l} .$

3. Chu kì, tần số, tần số góc: $T = 2 π \sqrt{\frac{l}{g}}$ ; $f = \frac{1}{2 π} \sqrt{\frac{g}{l}}$ ; $ω = \sqrt{\frac{g}{l}}$ .

Trong đó:

$g$ là gia tốc rơi tự do (m/s2),

$l$ là chiều dài của con lắc (m).

4. Năng lượng của con lắc đơn

- Động năng: $W_{đ} = \frac{1}{2} m v^{2}$ .

- Thế năng: $W_{t} = m g l (1 - c o s α)$

(mốc tính thế năng tại vị trí cân bằng)

- Cơ năng: $W = W_{đ} + W_{t} = m g l (1 - c o s α_{0})$ = hằng số

- Cơ năng của con lắc đơn được bảo toàn nếu bỏ qua lực ma sát.

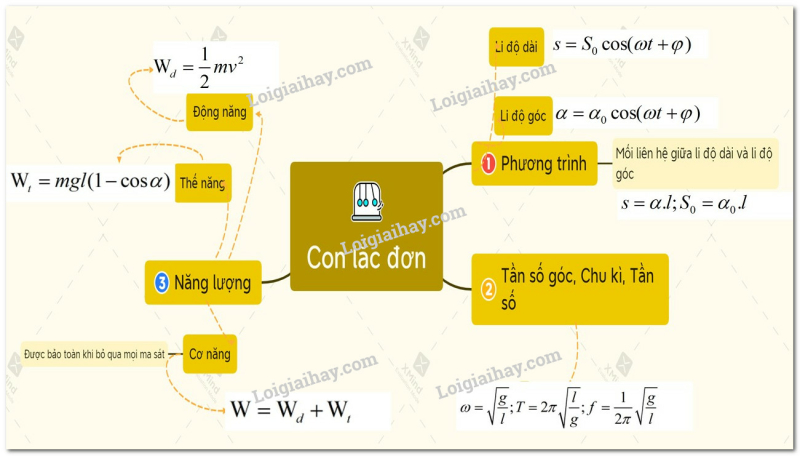
Sơ đồ tư duy về con lắc đơn

Xem thêm các chương trình khác:

Bài trước

Bài sau

Giải SGK, SBT, Chuyên đề Vật Lý Lớp 12