SBT Vật lí 12 Bài 2: Con lắc lò xo | Giải SBT Vật Lí lớp 12

Chúng tôi giới thiệu Giải sách bài tập Vật Lí lớp 12 Bài 2: Con lắc lò xo chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Vật Lí 12. Mời các bạn đón xem:

Bài giảng Vật Lí 12 Bài 2: Con lắc lò xo

Giải SBT Vật Lí 12 Bài 2: Con lắc lò xo

Bài 2.1 trang 6 SBT Vật Lí 12: Một lò xo giãn ra $2,5cm$ khi treo và nó một vật có khối lượng $250g$. Cho biết con lắc lò xo thẳng đứng dao động theo cùng quy luật với con lắc lò xo nằm ngang (lấy $g=10m/s^2$ ). Chu kì của con lắc được tạo thành như vậy là

A. $0,31s$         B. $10s$        

C. $1s$               D. $126s$

Phương pháp giải:

Sử dụng công thức tính độ biến dạng lò xo ở vị trí cân bằng: $\mathrm{\Delta }l={\displaystyle \frac{mg}{k}}$

Sử dụng công thức tính chu kì dao động: $T={\displaystyle \frac{2\pi }{\omega }}$

Lời giải:

Ta có độ biến dạng lò xo ở vị trí cân bằng: $\mathrm{\Delta }l={\displaystyle \frac{mg}{k}}(1)$

Mà $\omega =\sqrt{{\displaystyle \frac{k}{m}}}(2)$

Từ (1) và (2)$\Rightarrow \omega =\sqrt{{\displaystyle \frac{g}{\mathrm{\Delta }l}}}$

Chu kì: $T={\displaystyle \frac{2\pi }{\omega }}=2\pi \sqrt{{\displaystyle \frac{\mathrm{\Delta }l}{g}}}=2\pi \sqrt{{\displaystyle \frac{0,025}{10}}}=0,31(s)$

Chọn A

Bài 2.2 trang 6 SBT Vật Lí 12: Một con lắc lò xo dao động điều hòa theo trục $x$ nằm ngang. Lò xo có độ cứng$k=100N/m$. Khi vật có khối lượng $m$ của con lắc đi qua vị trí có li độ $x=-4cm$ thì thế năng của con lắc đó

A. $8J$              

B. $0,08J$        

C. $-0,08J$          

D. Không xác định được vì chưa biết giá trị của khối lượng $m$

Phương pháp giải:

Vận dụng công thức tính thế năng đàn hồi: ${\mathrm{W}}_t={\displaystyle \frac{1}{2}}k{x}^2$

Lời giải:

Thế năng đàn hồi của con lắc tại vị trí li độ $x=-4cm$ là: ${\mathrm{W}}_t={\displaystyle \frac{1}{2}}k{x}^2={\displaystyle \frac{1}{2}}.100.(-0,04{)}^2=0,08J$

Chú ý: Khi tính năng lượng li độ phải đổi sang đơn vị mét

Chọn B

Bài 2.3 trang 6 SBT Vật Lí 12: Một con lắc lò xo có khối lượng $m=0,5kg$ và độ cứng $k=60N/m$ . Con lắc dao động với biên độ bằng $5cm$. Tốc độ con lắc khi qua vị trí cân bằng là

A. $0,77m/s$         B. $0,17m/s$        

C. $0m/s$               D. $0,55m/s$

Phương pháp giải:

Sử dụng công thức tính tốc độ của vật trong dao động điều hòa

Lời giải:

Khi vật đi qua vị trí cân bằng thì tốc độ đạt cực đại: $v_{max}=A\omega$

Ta có$\{\begin{array}{l}A=5cm=0,05m\\ \omega =\sqrt{{\displaystyle \frac{k}{m}}}=\sqrt{{\displaystyle \frac{60}{0,5}}}=2\sqrt{30}rad/s\end{array}\Rightarrow v_{max}=A\omega =0,05.2\sqrt{30}\approx 0,55m/s$

Chú ý: Khi tính năng lượng, li độ phải đổi sang đơn vị mét.

Chọn D

Bài 2.4 trang 6 SBT Vật Lí 12: Một con lắc là xo có cơ năng $0,9J$ và biên độ dao động $A=15cm$. Động năng của con lắc tại li độ $x=-5cm$ là

A. $0,8J$      

B. $0,3J$        

C. $0,6J$    

D. Không xác định được vì chưa biết độ cứng của lò xo.

Phương pháp giải:

Sử dụng công thức tính động năng theo li độ: ${\mathrm{W}}_d={\displaystyle \frac{1}{2}}k(A^2-x^2)$

Lời giải:

Cơ năng của con lắc:$$\begin{gathered} \mathrm{W}={\displaystyle \frac{1}{2}}k{A}^2 \\ \Rightarrow k={\displaystyle \frac{2W}{A^2}}={\displaystyle \frac{2.0,9}{0,{15}^2}}=80(N/m) \end{gathered}$$

Động năng của vật tại li độ $x=-5cm$ là

$$\begin{gathered} {\mathrm{W}}_d={\displaystyle \frac{1}{2}}k(A^2-x^2) \\ ={\displaystyle \frac{1}{2}}.80.(0,{15}^2-(-0,05{)}^2)=0,8J \end{gathered}$$

Chú ý: Khi tính năng lượng li độ phải đổi sang đơn vị mét

Chọn A

Bài 2.5 trang 6 SBT Vật Lí 12: Một con lắc lò xo có độ cứng $k=200N/m$, khối lượng $m=200g$ dao động điều hòa với biên độ $A=10cm$. Tốc độ của con lắc khi qua vị trí có li độ $x=2,5cm$ là

A. $86,6m/s$              B. $3,06m/s$      

C. $8,67m/s$              D. $0,0027m/s$

Phương pháp giải:

Sử dụng công thức tính động năng theo li độ: ${\mathrm{W}}_d={\displaystyle \frac{1}{2}}k(A^2-x^2)$

Sử dụng công thức ${\mathrm{W}}_d={\displaystyle \frac{1}{2}}m{v}^2$

Lời giải:

Ta có

$$\begin{gathered} \{\begin{array}{l}{\mathrm{W}}_d={\displaystyle \frac{1}{2}}k(A^2-x^2)\\ {\mathrm{W}}_d={\displaystyle \frac{1}{2}}m{v}^2\end{array} \\ \Rightarrow v=\sqrt{{\displaystyle \frac{k}{m}}(A^2-x^2)} \\ =\sqrt{{\displaystyle \frac{200}{0,2}}(0,1^2-{0.025}^2)} \\ =3,06(m/s) \end{gathered}$$

Chọn B

Bài 2.6 trang 6 SBT Vật Lí 12: Con lắc lò xo gồm một vật nhỏ gắn với một lò xo nhẹ dao động điều hoà theo phương ngang. Lực kéo về tác dụng vào vật luôn

A. cùng chiều với chiều chuyển động của vật.

B. ngược chiều với chiều chuyển động của vật.

C. hướng về vị trí cân bằng.

D. hướng về vị trí biên

Phương pháp giải:

Sử dụng lí thuyết về lực kéo về

Lời giải:

Lực kéo về: $\overrightarrow{F}=m\overrightarrow{a}$, lực kéo về cùng hướng với gia tốc, luôn hướng về vị trí cân bằng

Chọn C

Bài 2.7 trang 7 SBT Vật Lí 12: Một con lắc lò xo gồm một vật nhỏ khối lượng $100g$ gắn với một lò xo nhẹ. Con lắc dao động điều hoà theo phương ngang với phương trình $x=10\cos 10\pi t(cm;s)$.  Mốc thế năng ở vị trí cân bằng. Lấy${\pi }^2=10$. Cơ năng của con lắc bằng

A.$0,50J$.                    B. $1,10J$.        

C. $1,00J$.                   D. $0,05J$.

Phương pháp giải:

Sử dụng công thức tính cơ năng của vật dao động điều hòa: $\mathrm{W}={\displaystyle \frac{1}{2}}k{A}^2$

Lời giải:

Đổi: $m=100g=0,1kg$

Từ phương trình: $x=10cos10\pi t$ (cm), ta có $A=10cm=0,1m$, $\omega =10\pi (rad/s)$

Ta có $\omega =\sqrt{{\displaystyle \frac{k}{m}}}\Rightarrow k=m.{\omega }^2$

Suy ra, cơ năng con lắc $\mathrm{W}={\displaystyle \frac{1}{2}}k{A}^2={\displaystyle \frac{1}{2}}m.{\omega }^2.A^2$

$={\displaystyle \frac{1}{2}}.0,1.(10\pi {)}^2.0,1^2=0,5J$

Chọn A

Bài 2.8 trang 7 SBT Vật Lí 12: Một con lắc lò xo có khối lượng vật nhỏ là$50g$ . Con lắc dao động điều hoà theo một trục cố định nằm ngang với phương trình$x=A\cos \omega t$. Cứ sau những khoảng thời gian $0,05s$ thì động năng và thế năng của vật lại bằng nhau. Lấy ${\pi }^2=10$. Lò xo của con lắc có độ cứng bằng

A. $25N/m$.                  B. $200N/m$.      

C. $100N/m$.                D. $50N/m$.

Phương pháp giải:

Khoảng thời gian giữa hai lần liên tiếp động năng bằng thế năng là ${\displaystyle \frac{T}{4}}$

Lời giải:

Thế năng tại li độ $x$: ${\mathrm{W}}_t={\displaystyle \frac{1}{2}}k{x}^2$

Động năng tại li độ $x$: ${\mathrm{W}}_d={\displaystyle \frac{1}{2}}k(A^2-x^2)$

Ta có $$ $\begin{array}{l}{W}_t={\mathrm{W}}_d\iff {\displaystyle \frac{1}{2}}k{x}^2={\displaystyle \frac{1}{2}}k(A^2-x^2)\iff x^2=(A^2-x^2)\iff x=\pm {\displaystyle \frac{A\sqrt{2}}{2}}\end{array}$

Từ vòng tròn lượng giác:

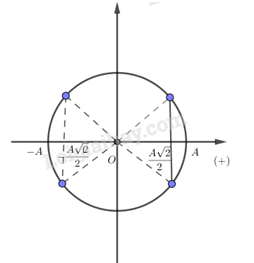
Ta tính được khoảng thời gian giữa lần động năng bằng thế năng là: $\omega t={\displaystyle \frac{\pi }{2}}\iff {\displaystyle \frac{2\pi }{T}}t={\displaystyle \frac{\pi }{2}}\iff t={\displaystyle \frac{T}{4}}(s)$

Suy ra ${\displaystyle \frac{T}{4}}=0,05\Rightarrow T=4.0,05=0,2(s)$

$\Rightarrow \omega =10\pi (rad/s)$

$\omega =\sqrt{{\displaystyle \frac{k}{m}}}$ 

$\Rightarrow k=m.{\omega }^2=0,05.(10\pi {)}^2=50(rad/s)$

Chọn D

Bài 2.9 trang 7 SBT Vật Lí 12: Một con lắc lò xo dao động điều hoà theo phương ngang với biên độ$10cm$. Mốc thế năng ở vị trí cân bằng. Cơ năng của con lắc là$200mJ$. Lò xo của con lắc có độ cứng là

A. $40N/m$.                 B. $50N/m$.      

C. $4N/m$.                   D. $5N/m$.

Phương pháp giải:

Sử dụng công thức tính cơ năng của con lắc: $\mathrm{W}={\displaystyle \frac{1}{2}}k{A}^2$

Lời giải:

Đổi:

$\begin{array}{l}A=10cm=0,1m\\ \mathrm{W}=200mJ=0,2J\end{array}$

Ta có cơ năng của con lắc

$\mathrm{W}={\displaystyle \frac{1}{2}}k{A}^2$

$\Rightarrow k={\displaystyle \frac{2W}{A^2}}={\displaystyle \frac{2.0,2}{0,1^2}}=40(N/m)$

Chọn A

Bài 2.10 trang 7 SBT Vật Lí 12: Một chất điểm dao động điều hoà trên trục $\mathrm{O}\mathrm{x}$. Trong các đại lượng sau của chất điểm: biên độ, vận tốc, gia tốc, động năng thì đại lượng nào không thay đổi theo thời gian?

A. Gia tốc.                        B. Vận tốc.           

C. Động năng.                  D. Biên độ.

Phương pháp giải:

Vận dụng lí thuyết về các đại lượng trong dao động điều hòa

Lời giải:

Vận tốc, gia tốc biến thiên điều hòa theo thời gian

Động năng biến thiên tuần hoàn theo thời gian

Biên độ là đại lượng không thay đổi theo thời gian

Chọn D

Bài 2.11 trang 7 SBT Vật Lí 12: Con lắc lò xo gồm lò xo nhẹ có độ cứng $50N/m$ và vật nhỏ có khối lượng $200g$ đang dao động điều hoà theo phương ngang. Lấy ${\pi }^2=10$. Tần số dao động của con lắc là

A. $5,00Hz$.                B. $2,50Hz$.          

C. $0,32Hz$.                D. $3,14Hz$.

Phương pháp giải:

Sử dụng biểu thức tính tần số dao động của con lắc lò xo:$f={\displaystyle \frac{1}{2\pi }}\sqrt{{\displaystyle \frac{k}{m}}}$

Lời giải:

Đổi: $m=200g=0,2kg$

Tần số dao động của con lắc lò xo:$f={\displaystyle \frac{1}{2\pi }}\sqrt{{\displaystyle \frac{k}{m}}}$ 

$={\displaystyle \frac{1}{2\sqrt{10}}}\sqrt{{\displaystyle \frac{50}{0,2}}}=2,5(Hz)({\pi }^2=10)$

Chọn B

Bài 2.12 trang 7 SBT Vật Lí 12: Một vật nhỏ có khối lượng $500g$ dao động điều hoà dưới tác dụng của một lực kéo về có biểu thức $F=-0,8\cos 4t(N)$. Biên độ dao động của vật là

A. $8cm$.                       B. $6cm$.          

C. $12cm$.                     D. $10cm$

Phương pháp giải:

Sử dụng biểu thức lực kéo về: $F=-kx$

Sử dụng công thức tính tần số góc: $\omega =\sqrt{{\displaystyle \frac{k}{m}}}$

Lời giải:

Ta có tần số góc $\omega =\sqrt{{\displaystyle \frac{k}{m}}}\Rightarrow k=m{\omega }^2$

$=0,{5.4}^2=8(N/m)$

Lực kéo về: $F=-kx\iff -0,8\cos 4t=-8.x$

$\iff x=0,1\cos 4t(m)$

Suy ra $A=0,1m=10cm$

Chọn D

Bài 2.13 trang 7 SBT Vật Lí 12: Một con lắc lò xo có khối lượng $m=50g$, dao động điều hòa trên trục $x$ với chu kì $T=0,2s$ và biên độ $A=0,2m$. Chọn gốc tọa độ $O$ tại vị trí cân bằng, gốc thời gian là lúc con lắc qua vị trí cân bằng theo chiều âm.

a) Viết phương trình dao động của con lắc.

b) Xác định độ lớn và chiều vecto vận tốc, gia tốc và lực kéo về tại thời điểm $t={\displaystyle \frac{3T}{4}}$

Phương pháp giải:

a) Vận dụng các bước viết phương trình dao động điều hòa: tìm $\omega$, tìm $A$, tìm pha ban đầu $\phi$

b) Thay thời gian $t$ vào phương trình vận tốc, gia tốc

Sử dụng công thức tính độ lớn lực kéo về: $F=m|a|$

Vận dụng đặc điểm hướng các đại lượng vận tốc, gia tốc và lực kéo về

Lời giải:

a) Viết phương trình dao động của vật

+ Tần số góc: $\omega ={\displaystyle \frac{2\pi }{T}}={\displaystyle \frac{2\pi }{0,2}}=10\pi (rad/s)$

+ Biên độ: $A=0,2m=20cm$

+ Tìm $\phi$:

$t=0\{\begin{array}{l}{x}_0=A\cos \phi =0\\ v=-A\omega \sin \phi <0\end{array}\iff \{\begin{array}{l}\phi =\pm {\displaystyle \frac{\pi }{2}}\\ \sin \phi >0\end{array}\iff \phi ={\displaystyle \frac{\pi }{2}}$

Vậy phương trình dao động: $x=20\cos (10\pi t+{\displaystyle \frac{\pi }{2}})(cm)$

b)

Tại thời điểm $t={\displaystyle \frac{3T}{4}}={\displaystyle \frac{3}{4}}.0,2=0,15s$

Li độ:$x=20\cos (10\pi t+{\displaystyle \frac{\pi }{2}})=20\cos (10\pi .0,15+{\displaystyle \frac{\pi }{2}})=20(cm)$

Vật ở vị trí biên dương

$\Rightarrow |v|=0$ đi theo chiều âm

$|a|=A{\omega }^2=0,2.(10\pi {)}^2=197(m/s^2)$ hướng về vị trí cân bằng

Lực kéo về: $F=m|a|=0,05.197=9,85N$

Lực kéo về có hướng cùng với hướng gia tốc nên lực kéo về cũng hướng về vị trí cân bằng.

Bài 2.14 trang 8 SBT Vật Lí 12: Một con lắc lò xo có biên độ $A=10,0cm$ , có tốc độ cực đại $1,2m/s$ và có cơ năng $1J$. Hãy tính:

a) Độ cứng của lò xo.

b) Khối lượng của quả cầu con lắc.

c) Tần số dao động của con lắc.

Phương pháp giải:

Vận dụng công thức tính cơ năng $\mathrm{W}={\displaystyle \frac{1}{2}}k{A}^2={\displaystyle \frac{1}{2}}m{v_{max}}^2$

Sử dụng công thức tính tần số dao động $f={\displaystyle \frac{1}{2\pi }}\sqrt{{\displaystyle \frac{k}{m}}}$

Lời giải:

Ta có: $A=10cm=0,1m$

a) $\mathrm{W}=W_{t_{max}}={\displaystyle \frac{1}{2}}k{A}^2$

$\Rightarrow k={\displaystyle \frac{2W}{A^2}}={\displaystyle \frac{2.1}{0,1^2}}=200(N/m)$

b)$\mathrm{W}={\mathrm{W}}_{d_{max}}={\displaystyle \frac{1}{2}}m{v}_{max}^2$

$\Rightarrow m={\displaystyle \frac{2W}{v_{max}^2}}={\displaystyle \frac{2.1}{1,2^2}}=1,39(kg)$

c) Tần số dao động: $f={\displaystyle \frac{1}{2\pi }}\sqrt{{\displaystyle \frac{k}{m}}}={\displaystyle \frac{1}{2\pi }}\sqrt{{\displaystyle \frac{200}{1,39}}}=1,9(Hz)$

Bài 2.15 trang 8 SBT Vật Lí 12: Một vật có khối lượng $10g$ dao động điều hòa với biên độ $24cm$ và chu kì $4,0s$. Tại thời điểm $t=0$, vật ở vị trí biên $x=-A$.

a) Viết phương trình dao động của vật.

b) Tính li độ, gia tốc và lực kéo về tại thời điểm $t=0,5s$.

c) Xác định thời điểm đầu tiên vật qua vị trí có li độ $x=-12cm$ và tốc độ của vật tại thời điểm đó.

Phương pháp giải:

a) Sử dụng các bước viết phương trình dao động điều hòa: tìm $\omega$, tìm $A$, tìm pha ban đầu $\phi$

b) Thay t vào biểu thức li độ, gia tốc, lực kéo về

c) Sử dụng vòng tròn lượng giác tính thời gian

Sử dụng công thức tính tốc độ $v=\omega \sqrt{A^2-x^2}$

Lời giải:

a) Viết phương trình dao động của vật

+ Tần số góc: $\omega ={\displaystyle \frac{2\pi }{T}}={\displaystyle \frac{2\pi }{4}}={\displaystyle \frac{\pi }{2}}(rad/s)$

+ Biên độ: $A=24cm$

+ Tìm $\phi$: $t=0:x_0=A\cos \phi =-A\iff \cos \phi =-1\iff \phi =\pi (rad)$

Vậy phương trình dao động: $x=24\cos ({\displaystyle \frac{\pi }{2}}t+\pi )(cm)$

b) Phương trình gia tốc: $a=-A{\omega }^2\cos (\omega t+\phi )=-12.({\displaystyle \frac{\pi }{2}}{)}^2\cos ({\displaystyle \frac{\pi }{2}}t+\pi )(cm/s^2)$

Tại thời điểm $t=0,5s$:

Li độ: $x=24\cos ({\displaystyle \frac{\pi }{2}}t+\pi )=24\cos ({\displaystyle \frac{\pi }{2}}.0,5+\pi )=-12\sqrt{2}(cm)$

Gia tốc: $a=-12.({\displaystyle \frac{\pi }{2}}{)}^2\cos ({\displaystyle \frac{\pi }{2}}t+\pi )$

$=-12.({\displaystyle \frac{\pi }{2}}{)}^2\cos ({\displaystyle \frac{\pi }{2}}.0,5+\pi )$

$=41,9(cm/s^2)$

Lực kéo về: $F=m|a|=0,01.0,419$

$=4,{19.10}^{-3}(N)$

c) Thời điểm đầu tiên vật đi qua li độ $x=-12cm$ là

Vị trí xuất phát: $x=-A$

Vị trí đích: $x=-12cm=-{\displaystyle \frac{A}{2}}cm$

Vẽ vòng tròn lượng giác:

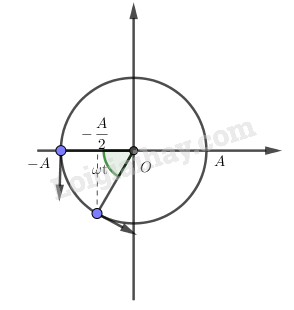
Từ hình vẽ: $\cos (\omega t)={\displaystyle \frac{1}{2}}$

$\Rightarrow \omega t={\displaystyle \frac{\pi }{3}}\iff {\displaystyle \frac{\pi }{2}}t={\displaystyle \frac{\pi }{3}}\iff t={\displaystyle \frac{2}{3}}s$

Tốc độ tại thời điểm đó: $v=\omega \sqrt{A^2-x^2}$

$={\displaystyle \frac{\pi }{2}}\sqrt{{24}^2-{(-12)}^2}=32,6(cm/s)$

Bài 2.16 trang 8 SBT Vật Lí 12: Một con lắc lò xo gồm một vật nhỏ khối lượng $200g$ gắn với một lò xo nhẹ, dao động điều hòa theo trục $\mathrm{O}\mathrm{x}$ nằm ngang với tần số $2,5Hz$. Trong khi dao động, chiều dài lò xo biến thiên từ $l_1=20cm$ đến $l_2=24cm$.

a) Tính biên độ dao động của vật và chiều dài của lò xo khi chưa biến dạng.

b) Viết phương trình dao động của vật, biết khi $t=0$ vật ở vị trí biên $x=+A$.

c) Tính vận tốc và gia tốc của vật khi vật đi qua vị trí cân bằng.

Phương pháp giải:

a) Sử dụng biểu thức độ dài quỹ đạo chuyển động của vật bằng khoảng biến thiên chiều dài của lò xo: $L=2A=l_2-l_1$

b) Vận dụng các bước viết phương trình dao động điều hòa: tìm $\omega$, tìm $A$, tìm pha ban đầu $\phi$

c) Sử dụng công thức tính vận tốc và gia tốc của vật dao động điều hòa

Lời giải:

a) Độ dài quỹ đạo chuyển động của vật bằng khoảng biến thiên chiều dài của lò xo:

$\begin{array}{l}L=2A=l_2-l_1=24-20=4cm\\ \Rightarrow A=2cm\end{array}$

Chiều dài tự nhiên $l_0=l_1+A=20+2=22cm$

b) Viết phương trình dao động của vật

+ Tần số góc: $\omega =2\pi f=2\pi .2,5=5\pi (rad/s)$

+ Biên độ: $A=2cm$

+ Tìm $\phi$: $t=0:x_0=A\cos \phi =A$

$\iff \cos \phi =1\iff \phi =0(rad)$

Vậy phương trình dao động: $x=2\cos (5\pi t)(cm)$

c) Khi vật đi qua vị trí cân bằng:

Vật tốc: $v=\pm A\omega =\pm 2.5\pi =\pm 10\pi (cm/s)$

Gia tốc: $a=0$

Chú ý:

Vận tốc có thể âm có thể dương, khi đi qua vị trí cân bằng theo chiều dương $v=A\omega$ còn khi đi qua vị trí cân bằng theo chiều âm $v=-A\omega$

Bài 2.17 trang 8 SBT Vật Lí 12: Một con lắc dao động điều hòa.

a) Tại li độ $x$ bằng một nửa biên độ thì bao nhiêu phần của cơ năng là thế năng? Bao nhiêu phần là động năng?

b) Tại li độ nào (tính theo biên độ) thì động năng bằng thế năng?

Phương pháp giải:

Sử dụng công thức tính động năng${\mathrm{W}}_d={\displaystyle \frac{1}{2}}k(A^2-x^2)$, thế năng ${\mathrm{W}}_t={\displaystyle \frac{1}{2}}k{x}^2$, cơ năng$\mathrm{W}={\displaystyle \frac{1}{2}}k{A}^2$

Lời giải:

a) Tại $x={\displaystyle \frac{A}{2}}$:

${\displaystyle \frac{{\mathrm{W}}_t}{W}}={\displaystyle \frac{{\displaystyle \frac{1}{2}}k{x}^2}{{\displaystyle \frac{1}{2}}k{A}^2}}={\left({\displaystyle \frac{x}{A}}\right)}^2$

$={\left({\displaystyle \frac{1}{2}}\right)}^2=0,25=25\mathrm{\%}$

Vậy li độ $x$ bằng một nửa biên độ thì $25\mathrm{\%}$ của cơ năng là thế năng, $75\mathrm{\%}$ là động năng

b) ${\mathrm{W}}_d={\mathrm{W}}_t\iff {\displaystyle \frac{1}{2}}k(A^2-x^2)={\displaystyle \frac{1}{2}}k{x}^2$

$\iff x=\pm {\displaystyle \frac{A\sqrt{2}}{2}}$

Bài 2.18 trang 8 SBT Vật Lí 12: Một con lắc lò xo gồm một vật có khối lượng $0,5kg$ gắn vào đầu tự do của một lò xo nhẹ có độ cứng $20N/m$. Con lắc dao động theo trục $\mathrm{O}\mathrm{x}$ nằm ngang với biên độ dao động là $3cm$. Tính:

a) Cơ năng của con lắc và tốc độ cực đại của vật.

b) Động năng và tốc độ cực đại của vật tại vị trí có li độ $2,0cm$ 

Phương pháp giải:

Sử dụng công thức tính động năng${\mathrm{W}}_d={\displaystyle \frac{1}{2}}k(A^2-x^2)={\displaystyle \frac{1}{2}}m{v}^2$, thế năng ${\mathrm{W}}_t={\displaystyle \frac{1}{2}}k{x}^2$, cơ năng $\mathrm{W}={\displaystyle \frac{1}{2}}k{A}^2$

Lời giải:

Cơ năng của con lắc: $\mathrm{W}={\displaystyle \frac{1}{2}}k{A}^2={\displaystyle \frac{1}{2}}.20.0,{03}^2={9.10}^{-3}J=9mJ$

Ta có: $\mathrm{W}={\displaystyle \frac{1}{2}}m{v}_{max}^2\Rightarrow v_{max}=\sqrt{{\displaystyle \frac{2W}{m}}}=\sqrt{{\displaystyle \frac{{\mathrm{2.9.10}}^{-3}}{0,5}}}=0.19m/s$

b) Tại li độ $x=2cm$

${\mathrm{W}}_d={\displaystyle \frac{1}{2}}k(A^2-x^2)$

$={\displaystyle \frac{1}{2}}.20.(0,{03}^2-0,02{}^2)$

$={5.10}^{-3}J=5mJ$

Ta có ${\mathrm{W}}_d={\displaystyle \frac{1}{2}}m{v}^2$

$\Rightarrow v=\sqrt{{\displaystyle \frac{2{\mathrm{W}}_d}{m}}}$

$=\sqrt{{\displaystyle \frac{{\mathrm{2.5.10}}^{-3}}{0,5}}}=0,14(m/s)$