Bài tập cuối tuần Toán lớp 7 - Tuần 13

PHIẾU HỌC TẬP TOÁN 7 TUẦN 13

Đại số 7 : § 3:  Đại lượng tỉ lệ nghịch

Hình học 7: § 4: Trường hợp bằng nhau thứ hai của tam giác c-g-c

†††††††††

Bài 1: Với cùng một số tiền để mua 225m vải loại 1 có thể mua được bao nhiêu m vải loại 2; biết rằng giá tiền vải loại 2 chỉ bằng 75% giá tiền vải loại 1

Bài 2: Cho 3 đại lượng x, y, z. Hãy cho biết mối liên hệ giữa hai đại lượng x và z biết:

a) x và y tỉ lệ nghịch; y và z tỉ lệ nghịch

b) x và y tỉ lệ nghịch; y và z tỉ lệ thuận

Bài 3: Các giá trị của 2 đại lượng x, y được cho trong bảng có phải là 2 đại lượng tỉ lệ nghịch không? Nếu có, hãy tìm hệ số tỉ lệ và biểu diễn y theo x

Bài 4: Cho $\Delta \mathrm{ABC}$ có $\mathrm{AB}=\mathrm{AC}$. Lấy điểm E trên cạnh AB, F trên cạnh AC sao cho AE=AF.

a) Chứng minh: $\mathrm{BF}=\mathrm{CE}$ và $\Delta \mathrm{BEC}=\Delta \mathrm{CFB}$.

b) BF cắt CE tại I, cho biết IE=IF. Chứng minh: $\Delta \mathrm{IBE}=\Delta \mathrm{ICF}$ bằng hai cách.

Bài 5:  Cho hai đoạn thẳng AB và CD cắt nhau tại trung điểm O của mỗi đoạn thẳng.

a) Chứng minh:  $\mathrm{AC}=\mathrm{DB}$ và $\mathrm{AC}//\mathrm{DB}$.

b) Chứng minh: $\mathrm{AD}=\mathrm{CB}$ và $\mathrm{AD}//\mathrm{CB}$.

c) Chứng minh: $\widehat{\mathrm{ACB}}=\widehat{\mathrm{BDA}}$.

d) Vẽ $\mathrm{CH}\perp \mathrm{AB}$ tại H. Trên tia đối của tia OH lấy điểm I sao cho $\mathrm{OI}=\mathrm{OH}$. Chứng minh: $\mathrm{DI}\perp \mathrm{AB}.$

Bài 6:  Cho $\Delta \mathrm{MNP}$ có $\mathrm{PM}=\mathrm{PN}$. Chứng minh: $\widehat{\mathrm{PMN}}=\widehat{\mathrm{PNM}}$ bằng hai cách.

PHẦN HƯỚNG DẪN GIẢI

Bài 1:  

Với số tiền không đổi thì số m vải mua được và giá vải là hai đại lượng tỉ lệ nghịch

Gọi số m vải loại 2 mua được là x, theo tính chất của đại lượng tỉ lệ nghịch, ta có

 $\frac{225}{x}=\frac{75}{100}$$\Rightarrow x=\frac{225.100}{75}=300$

Số mét vải loại 2 mua được là 300m.

Bài 2: a) x và y tỉ lệ nghịch $\Rightarrow xy=a$ $\left(a\ne 0\right)$  

y và z tỉ lệ nghịch $\Rightarrow yz=b\Rightarrow y=\frac{b}{z}$ $\left(b\ne 0\right)$   

Thay $y=\frac{b}{z}$ ta có $x.\frac{b}{z}=a\Rightarrow x=\frac{a}{b}z$

Vậy x và z là hai đại lượng tỉ lệ thuận theo hệ số $\frac{a}{b}$

b) x và y tỉ lệ nghịch $\Rightarrow xy=a$ $\left(a\ne 0\right)$ 

y và z tỉ lệ thuận$\Rightarrow y=kz$ $\left(k\ne 0\right)$

Thay $y=kz$ ta có $x.kz=a\Rightarrow xz=\frac{a}{k}$

Vậy x và z là hai đại lượng tỉ lệ thuận theo hệ số tỉ lệ $\frac{a}{k}$

Bài 3: Hai đại lượng x và y cho trong bảng là hai đại lượng tỉ lệ nghịch vì $- 3.30 = ( - 2).45 = 4.( - 22,5)$$= ( - 9).10 = 15.( - 6) = - 90$;

hệ số tỉ lệ $a=-90$ và biểu diễn y theo x là: $y=\frac{-90}{x}$

Bài 4:

a) Chứng minh: $\mathrm{BF}=\mathrm{CE}$ và $\Delta \mathrm{BEC}=\Delta \mathrm{CFB}$.

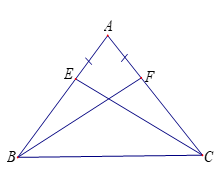
* Xét hai tam giác $\Delta \mathrm{BAF}$ và $\Delta \mathrm{CAE}$ có:

$\mathrm{BA}=\mathrm{CA}$ (gt)

$\hat{\mathrm{A}}$ chung

$\mathrm{AF}=\mathrm{AE}$ (gt)

$\Rightarrow \Delta \mathrm{BAF}$= $\Delta \mathrm{CAE}$ (c.g.c)

$\Rightarrow \mathrm{BF}=\mathrm{CE}$ (1)

Ta có: $\mathrm{AE}+\mathrm{EB}=\mathrm{AB}$

$\mathrm{AF}+\mathrm{FC}=\mathrm{AC}$

Mà $\mathrm{AB}=\mathrm{AC}$, $\mathrm{AE}=\mathrm{AF}$

$\Rightarrow \mathrm{EB}=\mathrm{FC}$ (2)

* Xét hai tam giác $\Delta \mathrm{BEC}$ và $\Delta \mathrm{CFB}$ có:

$\mathrm{BE}=\mathrm{CF}$ theo (2)

$\mathrm{EC}=\mathrm{FB}$ theo (1)

Cạnh BC chung

$\Rightarrow \Delta \mathrm{BEC}$ = $\Delta \mathrm{CFB}$ (c.c.c)

b) Chứng minh: $\Delta \mathrm{IBE}=\Delta \mathrm{ICF}$ bằng hai cách.

Ta có: $\mathrm{BI}+\mathrm{IF}=\mathrm{BF}$

$\mathrm{CI}+\mathrm{IE}=\mathrm{CE}$

Mặt khác, $\mathrm{BF}=\mathrm{CE}$, $\mathrm{IF}=\mathrm{IE}$

$\Rightarrow \mathrm{BI}=\mathrm{CI}$ (3)

Cách 1:

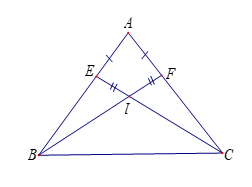
Xét hai tam giác $\Delta \mathrm{IBE}$ và $\Delta \mathrm{ICF}$ có:

IB=IC theo (3)

BE=CF theo (2)

IE=IF (gt)

$\Rightarrow ∆IBE=∆ICF$(c.c.c)

Tài liệu đầy đủ quý Thầy/Cô và bạn đọc vui lòng chọn mục tải xuống để xem chi tiết.