Bài toán về điểm biểu diễn số phức trong mặt phẳng

Đặt

$\begin{array}{l}z = a + bi;a,b \in R;{i^2} =  - 1\\ \Rightarrow z - i = a + \left( {b - 1} \right)i\\ \Rightarrow z - \overline z  + 2i = \left( {2 + 2b} \right)i\\ \Rightarrow \left| {z - \overline z  + 2i} \right| = 2\left| {z - i} \right| \Leftrightarrow \sqrt {{{\left( {2 + 2b} \right)}^2}}  = 2\sqrt {{a^2} + {{\left( {b - 1} \right)}^2}}  \\ \Leftrightarrow 4{a^2} - 16b = 0 \Leftrightarrow b = \dfrac{1}{4}{a^2}\end{array}$

Tập hợp các điểm biểu diễn số phức là đường parabol

Gọi \(z = x + yi\). Khi đó điểm $M\left( {x;y} \right)$ biểu diễn số phức$z$.

Ta có : \(\left| {z - 2} \right| + \left| {z + 2} \right| = 10 \Leftrightarrow \left| {x - 2 + yi} \right| + \left| {x + 2 + yi} \right| = 10 \)

$\Leftrightarrow \sqrt {{{\left( {x - 2} \right)}^2} + {y^2}}  + \sqrt {{{\left( {x + 2} \right)}^2} + {y^2}}  = 10$.

Đặt ${F_1}\left( { - 2;0} \right);{F_2}\left( {2;0} \right)$, khi đó : \(M{F_1} + M{F_2} = 10 > {F_1}{F_2}( = 4)\) nên tập hợp các điểm $M$ là elip $\left( E \right)$  có 2 tiêu điểm là ${F_1};{F_2}$ . Gọi $\left( E \right)$ có dạng : \(\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\)

Ta có \(\left\{ \begin{array}{l}M{F_1} + M{F_2} = 10 = 2a\\{F_1}{F_2} = 4 = 2c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 5\\c = 2\end{array} \right. \Rightarrow b = \sqrt {{5^2} - {2^2}}  = \sqrt {21} \)

Vậy tập hợp các điểm $M$ là elip : \((E):\dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{{21}} = 1\).      

Ta có \({z_1} = 3 - 2i,\) \({z_2} = 1 + 4i\) và \({z_3} =  - 1 + i\) có biểu diễn hình học trong mặt phẳng tọa độ Oxy lần lượt là các điểm \(A,B,C\) nên \(A\left( {3; - 2} \right);\,\,B\left( {1;4} \right);\,\,C\left( { - 1;1} \right).\)

Khi đó ta có:

$\begin{array}{l}
AB = \sqrt {{{\left( {1 - 3} \right)}^2} + {{\left( {4 + 2} \right)}^2}} = 2\sqrt {10} \\
AC = \sqrt {{{\left( { - 1 - 3} \right)}^2} + {{\left( {1 + 2} \right)}^2}} = 5\\
BC = \sqrt {{{\left( { - 1 - 1} \right)}^2} + {{\left( {1 - 4} \right)}^2}} = \sqrt {13}
\end{array}$

Gọi \(p\) là nửa chu vi tam giác \(ABC\) ta có: \(p = \dfrac{{2\sqrt {10}  + 5 + \sqrt {13} }}{2}.\)

Diện tích tam giác \(ABC\) là: \({S_{\Delta ABC}} = \sqrt {p\left( {p - AB} \right)\left( {p - AC} \right)\left( {p - BC} \right)}  = 9.\)

Ta có \(z = \left( {m + 3} \right) + \left( {{m^2} - m - 6} \right)i\) được biểu diễn bởi điểm \(M\left( {x;y} \right)\) với \(\left\{ \begin{array}{l}x = m + 3\\y = {m^2} - m - 6\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}m = x - 3\\y = {\left( {x - 3} \right)^2} - \left( {x - 3} \right) - 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = x - 3\\y = {x^2} - 7x + 6\end{array} \right.\).

Vậy tập hợp điểm biểu diễn số phức \(z\) là parabol \(\left( P \right):y = {x^2} - 7x + 6\)

Hoành độ giao điểm của parabol \(\left( P \right)\) với trục hoành là \({x^2} - 7x + 6 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 6\end{array} \right.\)

Diện tích hình phẳng giới hạn bởi \(\left( P \right)\) và trục hoành bằng

\(S = \int\limits_1^6 {\left| {{x^2} - 7x + 6} \right|dx}  = \left| {\int\limits_1^6 {\left( {{x^2} - 7x + 6} \right)dx} } \right| = \dfrac{{125}}{6}\)

Ta có: \(z =  - 1 + 2i\) có điểm biểu diễn là \(M\left( { - 1;\,\,2} \right).\)

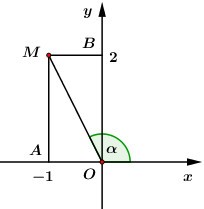
Ta có:  \(\tan AOM = \dfrac{{AM}}{{OA}} = \dfrac{2}{1} = 2.\)

\( \Rightarrow \tan \alpha  =  - \tan AOM =  - 2\) (hai góc bù nhau)

\( \Rightarrow \tan 2\alpha  = \dfrac{{2\tan \alpha }}{{1 - {{\tan }^2}\alpha }} = \dfrac{{2.\left( { - 2} \right)}}{{1 - {{\left( { - 2} \right)}^2}}} = \dfrac{4}{3}\)

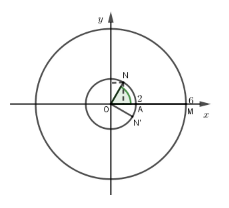
Ta chọn \({z_1} = 6\) có điểm biểu diễn là \(M\left( {6;0} \right)\).

Khi đó \(\widehat {MON} = {60^0}\) nên chọn \(N\left( {1;\sqrt 3 } \right)\) (hình vẽ) biểu diễn số phức \(i{z_2}\)

Suy ra điểm \(N'\left( {\sqrt 3 ; - 1} \right)\) biểu diễn số phức \({z_2}\) hay \({z_2} = \sqrt 3  - i\).

Khi đó \(T = \left| {z_1^2 + 9z_2^2} \right| = \left| {{6^2} + 9{{\left( {\sqrt 3  - i} \right)}^2}} \right| = 36\sqrt 3 \).

Ta có

\(\begin{array}{l}w = 2{z_1} - {z_2}\\\,\,\,\,\, = 2\left( {3 + i} \right) - \left( { - 1 + 2i} \right)\\\,\,\,\,\, = 6 + 2i + 1 - 2i = 7\end{array}\)

Vậy điểm biểu diễn của số phức \(w\) là \(M\left( {7;0} \right)\).

Bước 1:

Gọi \(z = x + yi\left( {x;y \in R} \right)\) khi đó \(\overline z  = x - yi\)

Bước 2:

Ta có: \(z.\overline z  = 1 \Leftrightarrow \left( {x + yi} \right)\left( {x - yi} \right) = 1\) \( \Leftrightarrow {x^2} - {\left( {yi} \right)^2} = 1\) \( \Leftrightarrow {x^2} + {y^2} = 1\)

Vậy tập hợp điểm biểu diễn số phức \(z\) là một đường tròn.