1. Hình nón, khối nón
a) Mặt nón tròn xoay
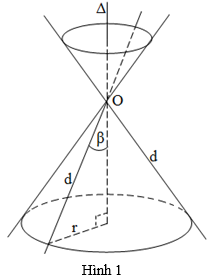
+ Trong mặt phẳng $\left( P \right),$ cho $2$ đường thẳng $d,\Delta $ cắt nhau tại $O$ và chúng tạo thành góc $\beta $ với $0 < \beta < {90^0}.$ Khi quay $mp\left( P \right)$ xung quanh trục $\Delta $ với góc $\beta $ không thay đổi được gọi là mặt nón tròn xoay đỉnh $O$ (hình 1).
+ Người ta thường gọi tắt mặt nón tròn xoay là mặt nón.
Đường thẳng $\Delta $ gọi là trục, đường thẳng d được gọi là đường sinh và góc $2\beta $ gọi là góc ở đỉnh.
b) Hình nón tròn xoay
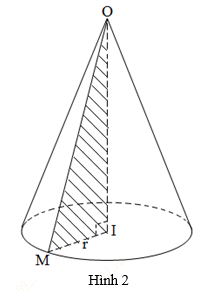
+ Cho $\Delta OIM$ vuông tại $I$ quay quanh cạnh góc vuông $OI$ thì đường gấp khúc $OIM$ tạo thành một hình, gọi là hình nón tròn xoay (gọi tắt là hình nón) (hình 2).
+ Đường thẳng $OI$ gọi là trục, $O$ là đỉnh, $OI$ gọi là đường cao và $OM$ gọi là đường sinh của hình nón.
+ Hình tròn tâm $I,$ bán kính $r = IM$ là đáy của hình nón.
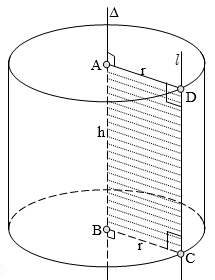
c) Công thức diện tích và thể tích của hình nón
Cho hình nón có chiều cao là $h,$ bán kính đáy $r$ và đường sinh là $\ell $ thì có:
+ Diện tích xung quanh:${S_{xq}} = \pi .r.l$
+ Diện tích đáy (hình tròn):${S_d} = \pi .{r^2}$
+ Diện tích toàn phần hình tròn: $S = {S_d}\; + {\rm{ }}{S_{xq}}$
+ Thể tích khối nón: \(V = \dfrac{1}{3}{S_d}.h = \dfrac{1}{3}\pi {r^2}h\)
d) Tính chất
Nếu cắt mặt nón tròn xoay bởi mặt phẳng đi qua đỉnh thì có các trường hợp sau xảy ra:
+ Mặt phẳng cắt mặt nón theo 2 đường sinh $ \to $ Thiết diện là tam giác cân.
+ Mặt phẳng tiếp xúc với mặt nón theo một đường sinh. Trong trường hợp này, người ta gọi đó là mặt phẳng tiếp diện của mặt nón.
Nếu cắt mặt nón tròn xoay bởi mặt phẳng không đi qua đỉnh thì có các trường hợp sau xảy ra:
+ Nếu mặt phẳng cắt vuông góc với trục hình nón$ \to $giao tuyến là một đường tròn.
+ Nếu mặt phẳng cắt song song với đường sinh hình nón$ \to $giao tuyến là $2$ nhánh của $1$
+ Nếu mặt phẳng cắt song song với $1$ đường sinh hình nón$ \to $giao tuyến là $1$ đường parabol.
2. Hình trụ, khối trụ
a) Mặt trụ tròn xoay
+ Trong $mp\left( P \right)$ cho hai đường thẳng $\Delta $ và $\ell $ song song nhau, cách nhau một khoảng $r.$ Khi quay $mp\left( P \right)$ quanh trục cố định $\Delta $ thì đường thẳng $\ell $ sinh ra một mặt tròn xoay được gọi là mặt trụ tròn xoay hay gọi tắt là mặt trụ.
+ Đường thẳng $\Delta $ được gọi là trục.
+ Đường thẳng $\ell $ được gọi là đường sinh.
+ Khoảng cách $r$ được gọi là bán kính của mặt trụ.
b) Hình trụ tròn xoay
+ Khi quay hình chữ nhật $ABCD$ xung quanh đường thẳng chứa một cạnh, chẳng hạn cạnh $AB$ thì đường gấp khúc $ABCD$ tạo thành một hình, hình đó được gọi là hình trụ tròn xoay hay gọi tắt là hình trụ.
+ Đường thẳng $AB$ được gọi là trục.
+ Đoạn thẳng $CD$ được gọi là đường sinh.
+ Độ dài đoạn thẳng $AB = CD = h$ được gọi là chiều cao của hình trụ.
+ Hình tròn tâm $A,$ bán kính $r = AD$ và hình tròn tâm $B,$ bán kính $r = BC$ được gọi là $2$ đáy của hình trụ.
+ Khối trụ tròn xoay, gọi tắt là khối trụ, là phần không gian giới hạn bởi hình trụ tròn xoay kể cả hình trụ.
c) Công thức tính diện tích và thể tích của hình trụ
Cho hình trụ có chiều cao là h và bán kính đáy bằng $r,$ khi đó:
+ Diện tích xung quanh của hình trụ: ${S_{xq}}\; = 2\pi rh$
+ Diện tích toàn phần của hình trụ:
+ Thể tích khối trụ: $V = Bh = \pi {r^2}h$
d) Tính chất
+ Nếu cắt mặt trụ tròn xoay (có bán kính là $r$) bởi một $mp\left( \alpha \right)$ vuông góc với trục $\Delta $ thì ta được đường tròn có tâm trên $\Delta $ và có bán kính bằng $r$ với $r$ cũng chính là bán kính của mặt trụ đó.
+ Nếu cắt mặt trụ tròn xoay (có bán kính là $r$) bởi một $mp\left( \alpha \right)$ không vuông góc với trục $\Delta $ nhưng cắt tất cả các đường sinh, ta được giao tuyến là một đường elíp có trụ nhỏ bằng $2r$ và trục lớn bằng \(\dfrac{{2r}}{{\sin \alpha }}\), trong đó $\varphi $ là góc giữa trục $\Delta $ và $mp\left( \alpha \right)$ với $0 < \varphi < {90^0}.$
Cho $mp\left( \alpha \right)$ song song với trục $\Delta $ của mặt trụ tròn xoay và cách $\Delta $ một khoảng $k.$
+ Nếu $k < r$ thì $mp\left( \alpha \right)$ cắt mặt trụ theo hai đường sinh $ \to $ thiết diện là hình chữ nhật.
+ Nếu $k = r$ thì $mp\left( \alpha \right)$ tiếp xúc với mặt trụ theo một đường sinh.
+ Nếu $k > r$ thì $mp\left( \alpha \right)$ không cắt mặt trụ.
3. Mặt cầu, khối cầu
a) Định nghĩa
+ Mặt cầu: \(S\left( {O;R} \right) = \left\{ {\left. M \right|OM = R} \right\}\)
+ Khối cầu: \(V\left( {O;R} \right) = \left\{ {\left. M \right|OM \le R} \right\}\)
b) Vị trí tương đối giữa mặt cầu và mặt phẳng
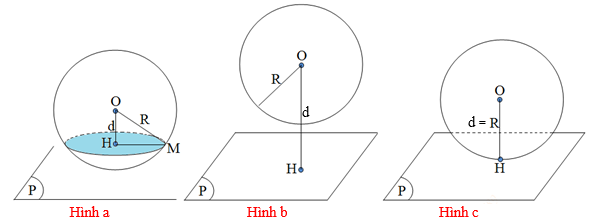
Cho mặt cầu $S\left( {O;R} \right)$ và mặt phẳng $\left( P \right).$ Gọi $d = d\left( {O;\left( P \right)} \right).$
+) Nếu $d < R$ thì $\left( P \right)$ cắt $\left( S \right)$ theo giao tuyến là đường tròn nằm trên $\left( P \right),$ có tâm $H$ và bán kính \(r = \sqrt {{R^2} - {d^2}} \)
+) Nếu $d = R$ thì $\left( P \right)$ tiếp xúc với $\left( S \right)$ tại tiếp điểm $H.$ ($\left( P \right)$ được gọi là tiếp diện của $\left( S \right)$)
+) Nếu $d > R$ thì $\left( P \right)$ và $\left( S \right)$ không có điểm chung.
Khi $d = 0$ thì $\left( P \right)$ đi qua tâm $O$ và được gọi là mặt phẳng kính, đường tròn giao tuyến có bán kính bằng $R$ được gọi là đường tròn lớn.
c) Vị trí tương đối giữa mặt cầu và đường thẳng
Cho mặt cầu $S\left( {O;R} \right)$ và đường thẳng $\Delta .$ Gọi $d = d(O;\Delta )$
+) Nếu $d < R$ thì $\Delta $ cắt $\left( S \right)$ tại hai điểm phân biệt.
+) Nếu $d = R$ thì $\Delta $ tiếp xúc với $\left( S \right)$. ($\Delta $ được gọi là tiếp tuyến của $\left( S \right)$)
+) Nếu $d > R$ thì $\Delta $ và $\left( S \right)$ không có điểm chung.
d) Mặt cầu ngoại tiếp – nội tiếp
e) Xác định tâm mặt cầu ngoại tiếp khối đa diện
+) Cách 1: Nếu $\left( {n - 2} \right)$ đỉnh của đa diện nhìn hai đỉnh còn lại dưới một góc vuông thì tâm của mặt cầu là trung điểm của đoạn thẳng nối hai đỉnh đó.
+) Cách 2: Để xác định tâm của mặt cầu ngoại tiếp hình chóp.
– Xác định trục $\Delta $ của đáy ($\Delta $ là đường thẳng vuông góc với đáy tại tâm đường tròn ngoại tiếp đa giác đáy).
– Xác định mặt phẳng trung trực $\left( P \right)$ của một cạnh bên.
– Giao điểm của $\left( P \right)$ và $\Delta $ là tâm của mặt cầu ngoại tiếp hình chóp.
f) Diện tích – Thể tích
