1. Hệ trục tọa độ trong không gian
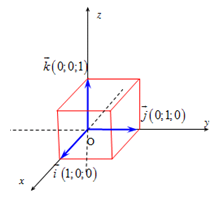
+) \({\overrightarrow i ^2} = {\overrightarrow j ^2} = {\overrightarrow k ^2} = 1\) và \(\overrightarrow i .\overrightarrow j = \overrightarrow i .\overrightarrow k \,\, = \,\,\overrightarrow k .\overrightarrow j = 0\)
+) $\vec 0 = (0;0;0),\,\,\vec i = (1;0;0),$ $\vec j = (0;1;0),\,\,\vec k = (0;0;1)$
2. Các công thức điểm, véc tơ
+) \(\vec a \pm \vec b\, = \,\,({a_1} \pm {b_1};\,\,{a_2} \pm {b_2};\,\,{a_3} \pm {b_3})\)
+) \(k\vec a\,\, = \,\,(k{a_1};\,\,k{a_2};\,\,k{a_3})\)
+) \(\overrightarrow a = \overrightarrow b \,\, \Leftrightarrow \,\,\left\{ \begin{array}{l}{a_1} = {b_1}\\{a_2} = {b_2}\\{a_3} = {b_3}\end{array} \right.\)
+) \(\overrightarrow a \) cùng phương \(\overrightarrow b \,(\vec b \ne \vec 0)\,\) \(\Leftrightarrow\overrightarrow a = k\overrightarrow b \,(k \in \mathbb{R})\)
\( \Leftrightarrow \,\,\left\{ \begin{array}{l}{a_1} = k{b_1}\\{a_2} = k{b_2}\\{a_3} = k{b_3}\end{array} \right. \Leftrightarrow \,\,\dfrac{{{a_1}}}{{{b_1}}} = \dfrac{{{a_2}}}{{{b_2}}} = \dfrac{{{a_3}}}{{{b_3}}},({b_1},\,\,{b_2},\,\,{b_3} \ne 0)\)
+) \(\vec a.\vec b = {a_1}.{b_1} + {a_2}.{b_2} + {a_3}.{b_3}\)
+) \(\overrightarrow a \bot \overrightarrow b \,\,\, \Leftrightarrow \,\,\,{a_1}{b_1} + {a_2}{b_2} + {a_3}{b_3} = 0\)
+) \({\vec a^2} = a_1^2 + a_2^2 + a_3^2\)
+) \(\left| {\vec a} \right| = \,\,\sqrt {a_1^2 + a_2^2 + a_2^2} \)
+) \(\cos (\vec a,\,\,\vec b)\,\, = \,\dfrac{{\vec a.\vec b}}{{\left| {\vec a} \right|.\left| {\vec b} \right|}}\,\, = \,\,\dfrac{{{a_1}{b_1} + {a_2}{b_2} + {a_3}{b_3}}}{{\sqrt {a_1^2 + a_2^2 + a_3^2} .\sqrt {b_1^2 + b_2^2 + b_3^2} }}\) (với \(\vec a,\,\,\vec b \ne \vec 0\))
+) \(M \in \left( {Oxy} \right) \Leftrightarrow z = 0;\) \(M \in \left( {Oyz} \right) \Leftrightarrow x = 0;\) \(M \in \left( {Oxz} \right) \Leftrightarrow y = 0\)
+)\(M \in Ox \Leftrightarrow y = z = 0;\) \(M \in Oy \Leftrightarrow x = z = 0;\) \(M \in Oz \Leftrightarrow x = y = 0\)
+) \(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A})\)
+) \(AB\,\, = \,\,\sqrt {{{({x_B} - {x_A})}^2} + {{({y_B} - {y_A})}^2} + {{({z_B} - {z_A})}^2}} \)
+) Toạ độ trung điểm \(M\)của đoạn thẳng \(AB\): \(M\left( {\dfrac{{{x_A} + {x_B}}}{2};\dfrac{{{y_A} + {y_B}}}{2};\dfrac{{{z_A} + {z_B}}}{2}} \right)\)
+) Toạ độ trọng tâm \(G\) của tam giác \(ABC\):
\(G\left( {\dfrac{{{x_A} + {x_B} + {x_C}}}{3};\dfrac{{{y_A} + {y_B} + {y_C}}}{3};\dfrac{{{z_A} + {z_B} + {z_C}}}{3}} \right)\)
+) Toạ độ trọng tâm \(G\) của tứ diện \(ABCD\):
\(G\left( {\dfrac{{{x_A} + {x_B} + {x_C} + {x_D}}}{4};\dfrac{{{y_A} + {y_B} + {y_C} + {y_D}}}{4};\dfrac{{{z_A} + {z_B} + {z_C} + {z_C}}}{4}} \right)\)
+) \(\,\left[ {\vec a,\vec b} \right]\,\, = \,\,\left( {\left| {\begin{array}{*{20}{c}}{{a_2}}&{{a_3}}\\{{b_2}}&{{b_3}}\end{array}} \right|\,\,;\,\,\left| {\begin{array}{*{20}{c}}{{a_3}}&{{a_1}}\\{{b_3}}&{{b_1}}\end{array}} \right|\,\,;\,\,\left| {\begin{array}{*{20}{c}}{{a_1}}&{{a_2}}\\{{b_1}}&{{b_2}}\end{array}} \right|} \right) = \left( {{a_2}{b_3} - {a_3}{b_2};{a_3}{b_1} - {a_1}{b_3};{a_1}{b_2} - {a_2}{b_1}} \right)\)
+) \([\overrightarrow a ,\,\,\overrightarrow b ]\,\, \bot \,\,\overrightarrow a ;[\overrightarrow a ,\,\,\overrightarrow b ]\,\, \bot \,\,\overrightarrow b \)
+) \(\left[ {\overrightarrow a ,\,\,\overrightarrow b \,} \right] = - \left[ {\overrightarrow b ,\overrightarrow a } \right]\)
+) \(\left[ {\vec i,\vec j} \right] = \vec k;\left[ {\vec j,\vec k} \right] = \vec i;\left[ {\vec k,\vec i} \right] = \vec j\)
+) \(\left| {[\overrightarrow a ,\,\overrightarrow b ]} \right|\,\, = \,\left| {\vec a} \right|.\left| {\vec b} \right|.\sin \left( {\vec a,\vec b} \right)\) (Chương trình nâng cao)
+) \(\overrightarrow a ,\,\,\overrightarrow b \) cùng phương \( \Leftrightarrow [\overrightarrow a ,\,\,\overrightarrow b ]\,\, = \,\,\overrightarrow 0 \) (chứng minh $3$ điểm thẳng hàng)
+) \(\vec a,\vec b,\vec c\) đồng phẳng \( \Leftrightarrow \left[ {\vec a,\vec b} \right].\vec c = 0\)
+) Diện tích hình bình hành \(ABCD\):
+) Diện tích tam giác \(ABC\): \({S_{\Delta ABC}} = \dfrac{1}{2}\left| {\left[ {\overrightarrow {AB} ,\,\,\overrightarrow {AC} } \right]} \right|\)
+) Thể tích khối hộp \(ABCDA'B'C'D'\): \({V_{ABCD.A'B'C'D'}}\,\, = \,\,\left| {[\overrightarrow {AB} ,\,\,\overrightarrow {AD} ].\overrightarrow {AA'} } \right|\)
+) Thể tích tứ diện \(ABCD\):\({V_{ABCD}} = \dfrac{1}{6}\left| {[\overrightarrow {AB} ,\,\,\overrightarrow {AC} ]\,.\overrightarrow {AD} } \right|\)
3. Phương trình mặt phẳng
+) Trong không gian \(Oxyz\), mọi mặt phẳng đều có dạng phương trình:
\(Ax + By + Cz + D = 0\,\,\)với\({A^2} + {B^2} + {C^2} \ne 0\)
+) Nếu mặt phẳng $(\alpha )$ có phương trình \(Ax + By + Cz + D = 0\,\,\)thì nó có một VTPT là $\overrightarrow n (A;\,B;\,C)$.
+) Phương trình mặt phẳng đi qua điểm ${M_0}({x_0};{y_0};{z_0})$ và nhận vectơ $\overrightarrow n (A;\,B;\,C)$ khác $\overrightarrow 0 $ là VTPT là: $A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0$.
+) Nếu $\overrightarrow n $ là một VTPT của mặt phẳng $(\alpha )$ thì \(k\overrightarrow n \,\)\(\,(k \ne 0)\) cũng là một VTPT của mặt phẳng$(\alpha )$
+) Một mặt phẳng được xác định duy nhất nếu biết một điểm nó đi qua và một VTPT của nó.
+) Nếu $\overrightarrow u ,\,\overrightarrow v $ có giá song song hoặc nằm trên mặt phẳng $(\alpha )$ thì $\overrightarrow n = {\rm{[}}\overrightarrow u ,\,\overrightarrow v {\rm{]}}$ là một VTPT của $(\alpha )$.
+) Khoảng cách từ điểm ${M_0}$ đến mặt phẳng $(\alpha )$ được tính: \(d({M_0},(\alpha )) = \dfrac{{|A{x_0} + B{y_0} + C{z_0} + D|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\)
+) Góc giữa $\left( \alpha \right)$ và $\left( \beta \right)$ bằng hoặc bù với góc giữa hai VTPT $\overrightarrow {{n_\alpha }} ,\overrightarrow {{n_\beta }} $. Tức là:
$\cos \left( {\left( \alpha \right),\left( \beta \right)} \right) = \left| {\cos \left( {\overrightarrow {{n_\alpha }} ,\overrightarrow {{n_\beta }} } \right)} \right| = \dfrac{{\left| {\overrightarrow {{n_\alpha }} .\overrightarrow {{n_\beta }} } \right|}}{{\left| {\overrightarrow {{n_\alpha }} } \right|.\left| {\overrightarrow {{n_\beta }} } \right|}} = \dfrac{{\left| {{A_1}{A_2} + {B_1}{B_2} + {C_1}{C_2}} \right|}}{{\sqrt {A_1^2 + B_1^2 + C_1^2} .\sqrt {A_2^2 + B_2^2 + C_2^2} }}$
+) $(\alpha ){\rm{//}}(\beta )$
$\dfrac{{{A_1}}}{{{A_2}}} = \dfrac{{{B_1}}}{{{B_2}}} = \dfrac{{{C_1}}}{{{C_2}}} \ne \dfrac{{{D_1}}}{{{D_2}}}$
+) $(\alpha ) \equiv (\beta )$ $\Leftrightarrow\dfrac{{{A_1}}}{{{A_2}}} = \dfrac{{{B_1}}}{{{B_2}}} = \dfrac{{{C_1}}}{{{C_2}}} = \dfrac{{{D_1}}}{{{D_2}}}$
+) $(\alpha )$ cắt $(\beta )$ $\Leftrightarrow\dfrac{{{A_1}}}{{{A_2}}} \ne \dfrac{{{B_1}}}{{{B_2}}}$ hoặc $\dfrac{{{B_1}}}{{{B_2}}} \ne \dfrac{{{C_1}}}{{{C_2}}}$ hoặc $\dfrac{{{A_1}}}{{{A_2}}} \ne \dfrac{{{C_1}}}{{{C_2}}}$
4. Phương trình đường thẳng
+) Phương trình tham số: \(\left\{ \begin{array}{l}x = {x_0} + {a_1}t\\y = {y_0} + {a_2}t\\z = {z_0} + {a_2}t\end{array} \right.;{\rm{ }}\left( {t \in \mathbb{R}} \right)\) với \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) là điểm đi qua và \(\overrightarrow u = \left( {{a_1};{a_2};{a_3}} \right)\) là VTCP \(\left( {{a_1}^2 + {a_2}^2 + {a_3}^2 \ne 0} \right)\)
+) Phương trình chính tắc: \(\dfrac{{x - {x_0}}}{{{a_1}}} = \dfrac{{y - {y_0}}}{{{a_2}}} = \dfrac{{z - {z_0}}}{{{a_3}}}\) với \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) là điểm đi qua và \(\overrightarrow u = \left( {{a_1};{a_2};{a_3}} \right)\) là VTCP \(\left( {{a_1}{a_2}{a_3} \ne 0} \right)\)
+) Gọi $\varphi $ là góc giữa hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\). Ta có: \(\cos \varphi = \dfrac{{\left| {\overrightarrow {{u_1}} .\overrightarrow {{u_2}} } \right|}}{{\left| {\overrightarrow {{u_1}} } \right|.\left| {\overrightarrow {{u_2}} } \right|}}\)
+) Gọi $\varphi $ là góc giữa đường thẳng \(\Delta \) và mặt phẳng \((\alpha )\). Ta có: \(\sin \varphi = \dfrac{{\left| {\overrightarrow {{u_\Delta }} .\overrightarrow {{n_\alpha }} } \right|}}{{\left| {\overrightarrow {{u_\Delta }} } \right|.\left| {\overrightarrow {{n_\alpha }} } \right|}}\)
+) Khoảng cách từ điểm \(M\) đến đường thẳng \(\Delta \) đi qua điểm \({M_0}\) và có vectơ chỉ phương \(\overrightarrow {{u_\Delta }} \)
\(d\left( {M,\Delta } \right) = \dfrac{{\left| {\left[ {\overrightarrow {{u_\Delta }} ,\overrightarrow {{M_0}M} } \right]} \right|}}{{\left| {\overrightarrow {{u_\Delta }} } \right|}}\)
+) Khoảng cách giữa hai đường thẳng chéo nhau:
\({\Delta _1}\) đi qua điểm \(M\) và có vectơ chỉ phương \(\overrightarrow {{u_1}} \)
\({\Delta _2}\) đi qua điểm \(N\) và có vectơ chỉ phương \(\overrightarrow {{u_2}} \)
\(d\left( {{\Delta _1},{\Delta _2}} \right){\rm{ = }}\dfrac{{\left| {\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right].\overrightarrow {MN} } \right|}}{{\left| {\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right]} \right|}}\)
+) Vị trí tương đối của hai đường thẳng
$d$ song song $d'$ $\Leftrightarrow\left\{ \begin{array}{l}\overrightarrow u = k\overrightarrow {u'} \\M \in d,M \notin d'\end{array} \right.$
$d$ trùng $d'$ $\Leftrightarrow\left\{ \begin{array}{l}\overrightarrow u = k\overrightarrow {u'} \\M \in d,M \in d'\end{array} \right.$
$d$ cắt $d'$ $\Leftrightarrow\left[ {\overrightarrow u ,\overrightarrow {u'} } \right].\overrightarrow {MN} = 0$ và \(\overrightarrow u ,\overrightarrow {u'} \) không cùng phương
$d$ chéo $d'$ $\Leftrightarrow\left[ {\overrightarrow u ,\overrightarrow {u'} } \right].\overrightarrow {MN} \ne 0$
5. Phương trình mặt cầu
+) Phương trình chính tắc
Mặt cầu $\left( S \right):$\({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\) có tâm $I\left( {a;b;c} \right)$, bán kính $R > 0$
+) Phương trình tổng quát
Mặt cầu $\left( S \right):{x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0$ có tâm $I\left( {a;b;c} \right)$ và bán kính $R = \sqrt {{a^2} + {b^2} + {c^2} - d} $ với ${a^2} + {b^2} + {c^2} - d > 0$

